Синтаксичний розбір. Лівий і правий висновок. Неоднозначні та еквівалентні граматики. Способи завдання схем граматик. Рекомендації з побудови граматик. Опис списків. Приклад побудови граматик
Приклади граматик і мов
Співвідношення між типами мов
1. Кожна регулярна мова є КВ-мовою, але існують КВ-мови, що не є регулярними (наприклад, L={anbn | n>0}).
2. Кожна КВ-мова є КЗ-мовою, але існують КЗ-мови, що не є КВ-мовами (наприклад, L={anbncn | n>0});
3. Кожна КЗ-мова є мовою типу 0.
Зауваження: УКВ-мова, що містить порожній ланцюжок, не є КЗ-мовою.
Зауваження: варто підкреслити, якщо мова задана граматикою типу k, то це не означає, що не існує граматики типу k| (k|>k), що описує ту саму мову. Тому, коли говорять про мову типу k, звичайно мають на увазі максимально можливий номер k.
Наприклад: КЗ-граматикаG1=({0,1},{A,S},P1,S) і КВ-граматика G2=({0,1},{S}, P2, S),
де
Р1: S 0A1
0A1
0A 00A1
00A1
A
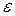
P2: S 0S1 | 01
0S1 | 01
описують ту саму мову L=L(G1)=L(G2)={0n1n | n>0}.
Мову L називають КВ-мовою, тому, що існує КВ-граматика, що її описує. Але вона не є регулярною мовою тому, що не існує регулярної граматики, що описує цю мову.
Зауваження: якщо при описі граматики зазначені тільки правила висновку Р, то будемо вважати, що великі латинські букви позначають нетермінальні символи, S – ціль граматики, всі інші символи термінальні.
1. Мова типу 0: 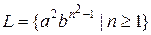
G(L): 
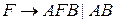
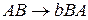
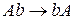
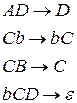
2. Мова типу 2: L={ланцюжок з 0 і 1 з однаковим числом 0 і 1}
G(L): 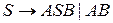
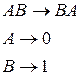
3. Мова типу 2: 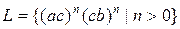
G(L): 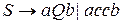
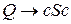
4. Мова типу 3: 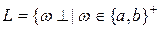 , де немає двох
, де немає двох  , що знаходяться поруч}
, що знаходяться поруч}
G(L): 
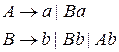
Ланцюжок належить мові, породженою граматикою, тільки у тому випадку, якщо існує її висновок з мети цієї граматики. Процес побудови такого висновку (а, отже, і визначення належності ланцюжка мові), називається розбором.
З практичної точки зору найбільший інтерес представляє розбір за контекстно-вільними граматиками (КВ чи УКВ). Їхньої породжуючої потужності досить для опису більшої частини синтаксичної структури мов програмування, для різних підкласів КВ-граматик є добре розроблені практично прийнятні способи рішення задачі розбору.
Розглянемо основні визначення, пов‘язані з розбором за КВ-граматикою.
Висновок ланцюжка 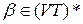 з
з 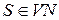 у КВ-граматиці G=(VT, VN, P, S), називається лівим (лівостороннім), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого лівого нетермінала.
у КВ-граматиці G=(VT, VN, P, S), називається лівим (лівостороннім), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого лівого нетермінала.


 0A1
0A1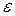
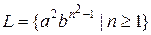

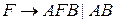
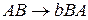
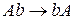
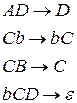
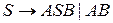
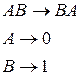
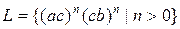
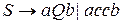
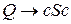
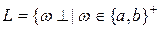 , де немає двох
, де немає двох  , що знаходяться поруч}
, що знаходяться поруч}
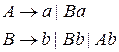
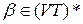 з
з 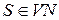 у КВ-граматиці G=(VT, VN, P, S), називається лівим (лівостороннім), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого лівого нетермінала.
у КВ-граматиці G=(VT, VN, P, S), називається лівим (лівостороннім), якщо у цьому висновку кожна чергова сентенціальна форма виходить з попередньої заміною самого лівого нетермінала.