Тип 3
Де , .
Де , .
Тип 2
Тип 1
Тип 0
Порожня мова. Типи формальних мов і граматик. Граматики типу 0. Граматики типу 1. Граматики типу 2. Граматики типу 3. Висновок у КС-граматиках і правила побудови дерева висновку
P1: 0A1 P2:S0S1|e
L(G1) = L(G2) = {0n1n |n>0}.
P1: 0A1 P2:S0S1|01
0A 00A1
00A1
A e
e
еквівалентні, тому що їх обидві породжує мова:
Граматики G1 і G2 майже еквівалентні, якщо L(G1)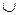 {e}=L(G2)
{e}=L(G2)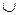 {e}.
{e}.
Іншими словами, граматики майже еквівалентні, якщо мови, ними породжувані, відрізняються не більше ніж на {e}.
Наприклад:
G1=({0,1}},{A, S}, P1, S) i G2=({0,1},{S}, P2, S),
де
0A 00A1
00A1
A e
e
Майже еквівалентні, тому що:
L(G1)={0n1n |n>0}, а L(G2)={0n1n |n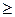 0},
0},
тобто L(G2) складається з усіх ланцюжків мови L(G1) і порожнього ланцюжка, що у L(G1) не входить.
Якщо мова, породжена граматикою G, не містить жодного скінченого ланцюжка то вона називається порожньою.
Для того, щоб мова L(G) не була порожньою, у множині Р має бути хоча б одне правило вигляду:
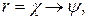
де 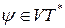
і має існувати висновок:
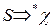 .
.
Класифікація мов за Хомським
Граматика G= (VT, VN, P, S) називається граматикоютипу 0, якщо на правила висновку не накладається жодних обмежень (крім тих, які зазначені у визначенні граматики).
Будь-яке правило  може бути побудованим з використанням довільних ланцюжків
може бути побудованим з використанням довільних ланцюжків 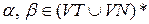 .
.
Граматика G= (VT, VN, P, S) називається граматикою, що не укорочує, якщо, кожне правило з множини Р має вигляд  ,
,
де 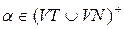 ,
, 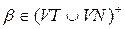 та
та  .
.
Граматика G= (VT, VN, P, S) називається контекстно-залежною (КЗ), якщо кожне правило з множини Р має вигляд  ,
,
де 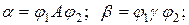
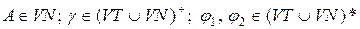 .
.
Граматику типу 1 можна визначити як неукорочуючу, так і як контексно-залежну. Вибір визначення не впливає на множину мов, породжуваних граматиками цього класу, оскільки доведено, що множина мов, породжуваних граматиками, що не укорочують, збігається з множиною мов, породжуваних КЗ-граматиками.
Граматика типу 1 значно зручніша на практиці, ніж граматика типу 0, оскільки в лівій частині правила замінюється завжди один нетермінальний символ, котрий можна пов‘язати з певним синтаксичним поняттям, в той час, як у граматиці типу 0 можна замінювати одразу кілька символів, у тому числі і термінальних.
Наприклад:
граматика G4:
VT={a,b,c,d}, VN{<I>, <A>, <B>}
R={<I> aA<I>,
aA<I>,
A<I> AA<I>,
AA<I>,
AAA A<B>A,
A<B>A,
A b,
b,
b<B>A bcdA,
bcdA,
b<I> ba}
ba}
є контекстно-залежною, оскільки друге та шосте правила мають непустий лівий контекст, а третє та п‘яте правило містять обидва контексти. Висновок у такій граматиці може мати вигляд:
<I>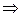 a<A><I>
a<A><I>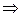 a<A><A><I>
a<A><A><I>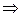 ab<A><I>
ab<A><I>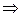 abb<I>
abb<I>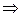 abba.
abba.
Граматика G=(VT, VN, P, S) називається контекстно-вільною (КВ), якщо кожне правило з множини Р має вигляд 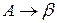 ,
,
Граматика G=(VT, VN, P, S) називається укорочуючою контекстно-вільною (УКВ), якщо кожне правило з множини Р має вигляд 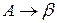 ,
,
Граматику типу 2 можна визначити як контекстно-вільну або укорочуючу контекстно-вільну.
Можливість вибору обумовлена тим, що для кожної УКВ-граматики існує майже еквівалентна КВ-граматика.
Граматика G=(VT, VN, P, S) називається праволінійною, якщо кожне правило з множини Р має вигляд 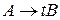 або
або 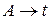 ,
,
де А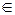 VN, B
VN, B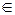 VN, t
VN, t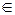 VT.
VT.
Граматика G=(VT, VN, P, S) називається ліволінійною, якщо кожне правило з множини Р має вигляд 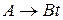 або
або 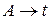 ,
,
де А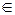 VN, B
VN, B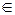 VN, t
VN, t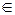 VT.
VT.
Граматику типу 3 (регулярну, Р-граматику) можна визначити як праволінійну або ліволінійну.
Вибір визначення не впливає на множину мов, породжуваних граматиками цього класу, оскільки доведено, що множина мов, породжуваних праволінійними граматиками, збігається з множиною мов, породжуваних ліволінійними граматиками.
Приклади правосторонньої та лівосторонньої граматики:
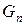 :
:
VT={a,b}, VN={<I>,<A>}, P={<I> a<I>,
a<I>,
<I> a<A>,
a<A>,
<A> b<A>,
b<A>,
<A> b<Z>,
b<Z>,
<Z>
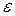 }
}
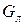 :
:
VT={a,b}, VN={<I>,<A>}, P={<I> <A>b,
<A>b,
<A> <A>b,
<A>b,
<A> <Z>a,
<Z>a,
<Z> <Z>a,
<Z>a,
<Z>
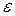 }.
}.
1. Будь-яка регулярна граматика є КВ-граматикою;
2. Будь-яка регулярна граматика є УКВ-граматикою;
3. Будь-яка КВ-граматика є КЗ-граматикою;
4. Будь-яка КВ-граматика є граматикою, що не укорочує;
5. Будь-яка КЗ-граматика є граматикою типу 0;
6. Будь-яка граматика, що не укорочує, є граматикою типу 0.
Зауваження: УКВ-граматика, що містить правила виду А
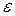 , не є КЗ-граматикою і не є граматикою, що не укорочує.
, не є КЗ-граматикою і не є граматикою, що не укорочує.
МоваL(G)є мовою типу k, якщо її можна описати граматикою типу k.


 00A1
00A1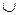 {e}=L(G2)
{e}=L(G2)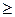 0},
0},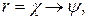
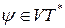
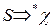 .
. може бути побудованим з використанням довільних ланцюжків
може бути побудованим з використанням довільних ланцюжків 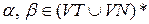 .
. ,
,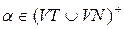 ,
, 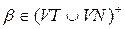 та
та  .
.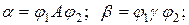
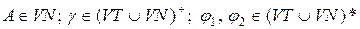 .
.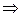 a<A><I>
a<A><I>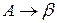 ,
,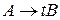 або
або 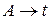 ,
,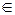 VN, B
VN, B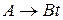 або
або 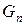 :
: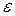 }
}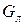 :
: