Рекомендована література
ПЛАН ЛЕКЦІЇ
Навчальний час(години, на які разрахована тема)2 год.
ЛЕКЦІЯ №3
Хмельницький 2012
Секретар засідання_______________Хрущ Л.Ф.
Викладач_____________________Гнатчук Є. Г.
Зав. кафедри ________________ Поморова О.В.
Протокол № 7
Засіданні кафедри
Заслухано та затверджено на
Для студентів 4 курсу
З навчальної дисципліни
КУРС ЛЕКЦІЙ
Кафедра системного програмування
ХМЕЛЬНИЦЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ
МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ, МОЛОДІ ТА СПОРТУ
«Основи теорії компіляції»
напряму «Комп’ютерна інженерія»
5 січня 2012 року,
з «Основи теорії компіляції»
(назва дисципліни)
Формальні граматики і мови. Первинні поняття.
Типи формальних мов і граматик
(тема лекції)
3.1 . Визначення формальної граматики і мови. Первинні поняття. Приклади, що ілюструють первинні поняття.
3.2 . Порожня мова. Типи формальних мов і граматик. Граматики типу 0. Граматики типу 1. Граматики типу 2. Граматики типу 3. Висновок у КС-граматиках і правила побудови дерева висновку.
3.3 . Синтаксичний розбір. Ліве і праве виведення. Неоднозначні й еквівалентні граматики. Способи завдання схем граматик. Рекомендації з побудови граматик. Опис списків. Приклад побудови граматик.
1. Джулій В.М., Савенко О.С., Муляр І.В. Системне програмне забезпечення: Навчальний посібник.- Хмельницький: ТУП, 2003 – 270с. (С. 48-52).
2. А.Ахо, Р. Сети, Д.Ульман Компиляторы. Принципы, технологии, инструменты. Пер. с англ. – Издательский дом «Вильямс», 2003. – 768с. (С. 44-56).
3. Волкова И.А Руденко Т.В. Формальные грамматики и языки. Элементы теории трансляции. Издательский отдел МГУ им. Ломоносова. – 2001. – 99 с. (С. 3-18).
4. Пратт Т., Зелковиц М. Языки программирования: разработка и реализация. Издательство: Питер, 2002. – 688 с.
5. Антонов А.В. Системный анализ. Учебник для вузов. -М.: Высшая школа, 2004. – 454 с.
6. Мозговой М.В. Классика программирования: алгоритмы, языки, автоматы, компиляторы. Практический подход. Издательство: Наука и Техника, 2006. – 320 с.
7. Веревкин А. П., Кирюшин О.В. Теория систем. Издательство: УГНТУ, 2003. – 100 с.
Словник чи алфавіт – це кінцева множина неподільних у поточному розрізі символів. Символи, що входять до алфавіту називають літерами алфавіту.
Наприклад: алфавіт А={a,b,c,+,1} містить 5 літер, а алфавіт B={00,01,10,11} містить 4 літери, кожна з яких складається з двох символів.
Ланцюжком символів або словомв алфавіті називається будь-яка скінчена послідовність літер цього алфавіту, а кількість літер, з яких складається слово, називають довжиною слова. Порожнім ланцюжком називається ланцюжок, що не містить жодного символу. Для позначення його будемо використовувати символ e.
Більш формально ланцюжок символів в алфавіті V визначається у такий спосіб.
1. e - ланцюжок в алфавіті V.
2. Якщо a- ланцюжок в алфавіті V і a – символ цього алфавіту, то aa – ланцюжок в алфавіті V.
3. b - ланцюжок в алфавіті V тоді і тільки тоді, коли він є такий в силу п.п.1 та 2.
Якщо a і b ланцюжки, то ab - називається конкатенацією (чи зчепленням) ланцюжків a і b.
Наприклад, якщо:
a = ab і b=cd, то ab=abcd.
Для будь-якого ланцюжка a вірний вираз:
ae=ea=a.
Реверсомланцюжка a називається ланцюжок, символи якого записані в зворотному порядку.
Реверс ланцюжка a будемо позначати aR. Наприклад, якщо:
a=abcdef, то aR=fedcba.
Для порожнього ланцюжка:
e=eR.
n-мступенем ланцюжка a (будемо позначати an) називається конкатенація n ланцюжків a:
a0=e; an=aan-1=an-1a.
Довжину ланцюжка a будемо позначати 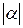 . Довжина e=0.
. Довжина e=0.
Мова в алфавіті V – це підмножина скінчених ланцюжків в цьому алфавіті.
Позначимо через V* множину, що містить усі ланцюжки в алфавіті V, включаючи порожній ланцюжок e.
Наприклад, якщо:
V={0,1}, то V*={e, 0, 1, 00, 01, 11, 10, 000, 001, 011,…}.
Позначимо через V+ множину, що містить усі ланцюжки в алфавіті V крім порожнього ланцюжка e.
Отже:

Декартовим добутком A´B множин A та B називається множина:
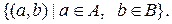
Зрозуміло, що кожна мова в алфавіті V є підмножиною множини V*.
Відомо кілька різних способів опису мов. Один з них використовує породжуючі граматики.
Формальною породжуючою граматикою G називають наступну четвірку об’єктів:
G=(VT, VN, P, S),
де:
VT – алфавіт термінальних символів (терміналів). Літери цього алфавіту називаються термінальними символами, з них будуються ланцюжки, що породжуються граматикою;
VN – алфавіт нетермінальних символів (не терміналів), що не перетинається з VT. Літери цього алфавіту використовуються при побудові ланцюжків. Вони можуть входити у проміжкові ланцюжки, але не повинні входити у результат породження;
P – множина правил висновку чи породжуючих правил наступного виду:  , де a і b - ланцюжки, побудовані з літер алфавіту
, де a і b - ланцюжки, побудовані з літер алфавіту 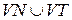 , який має назву повний алфавіт (словник) граматики G.
, який має назву повний алфавіт (словник) граматики G.
S – початковий символ граматики, 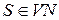 .
.
У множині правил граматики можуть зустрічатися правила з пустою правою частиною 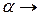 , тому, для уникнення невизначеності домовимось записувати таке правило у вигляді:
, тому, для уникнення невизначеності домовимось записувати таке правило у вигляді: 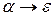 .
.
Для запису правил висновку з однаковими лівими частинами:
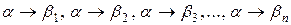
будемо користуватися скороченим записом:

Кожне bі (і = 1, 2, ..., n) будемо називати альтернативою правила висновку з ланцюжка a.
Приклад граматики:
G1= ({0,1}, {A, S}, P, S),
де P складається з правил:
S 0A1
0A1
0A 00A1
00A1
A e.
e.
Визначення.
Нехай r = t g правило граматики G і a=c/ t c// - ланцюжок символів, причому
g правило граматики G і a=c/ t c// - ланцюжок символів, причому 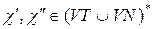 .
.
Тоді ланцюжок b=c/ g c// може бути отриманим з ланцюжка a шляхом застосування правила r (тобто заміною в ланцюжку t на g).
У цьому випадку кажуть, що ланцюжок b безпосередньо виведений з ланцюжка a та позначають 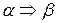 .
.
Наприклад:
ланцюжок 00А11 безпосередньо виведений з 0А1 у граматиці G1.
Якщо задана послідовність ланцюжків W = (v0, v1, … vn) таких, що існує послідовність безпосередніх виведень:
v0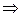 v1, v1
v1, v1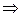 v2, ..., vn-1
v2, ..., vn-1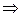 vn,
vn,
то таку послідовність називають виведенням довжини n vn з v0 в граматиці G та позначають v0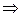 *vn.
*vn.
Наприклад:
S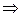 000A111 у граматиці G1, тому що існує виведення S
000A111 у граматиці G1, тому що існує виведення S 0A1
0A1 00A11
00A11 000A111. Довжина виведення – 3.
000A111. Довжина виведення – 3.
Мовою, що породжена граматикою G=(VT, VN, P, S), називається множина L(G)= {a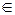 VT*½S
VT*½S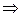 a}.
a}.
Іншими словами, L(G), це всі ланцюжки в алфавіті VT, що виведені з S за правилами P.
Наприклад:
L(G1)={0n1n |n>0}.
Ланцюжок a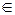 (VT
(VT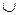 VN)*, для якої S
VN)*, для якої S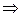 a, називається сентенціальноюформою в граматиці G=(VT, VN, P, S).
a, називається сентенціальноюформою в граматиці G=(VT, VN, P, S).
Таким чином, мову, яку складає граматика можна визначити як множину термінальних сентиціальних форм.
Граматики G1 і G2 називаються еквівалентними, якщо L(G1)=L(G2).
Наприклад:
G1=({0,1},{A, S}, P1, S) i G2=({0,1},{S}, P2, S),
де


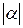 . Довжина e=0.
. Довжина e=0.
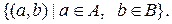
 , де a і b - ланцюжки, побудовані з літер алфавіту
, де a і b - ланцюжки, побудовані з літер алфавіту 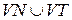 , який має назву повний алфавіт (словник) граматики G.
, який має назву повний алфавіт (словник) граматики G.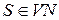 .
.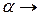 , тому, для уникнення невизначеності домовимось записувати таке правило у вигляді:
, тому, для уникнення невизначеності домовимось записувати таке правило у вигляді: 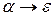 .
.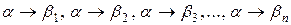

 0A1
0A1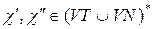 .
.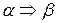 .
.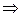 v1, v1
v1, v1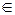 VT*½S
VT*½S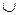 VN)*, для якої S
VN)*, для якої S