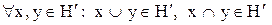 .
.
Визначення 6.5.Інтервалом 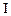 називається підструктури
називається підструктури 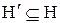 з найменшим елементом
з найменшим елементом 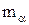 і найбільшим елементом
і найбільшим елементом  :
:  .
.
Визначення 6.6.Нульовий і одиничний елементи в структурі називаються структурними нулем і одиницею.
Визначення 6.7.У структурі 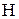 зі структурними нулем і одиницею два елементи
зі структурними нулем і одиницею два елементи 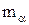 ,
,  називаються додатковими, якщо
називаються додатковими, якщо  ,
,  .
.
Визначення 6.8.Елемент 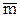 , додатковий до елемента
, додатковий до елемента 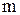 , називається доповненням елемента
, називається доповненням елемента 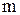 в структурі
в структурі 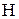 .
.
Визначення 6.9.Два елементи, що мають спільне доповнення у структурі 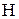 , називаються зв'язаними в
, називаються зв'язаними в 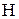 .
.
Приклад 6.3. У структурі 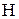 із приклада 6.2 (див. рис. 6.2) підструктурою
із приклада 6.2 (див. рис. 6.2) підструктурою 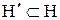 є сукупність елементів
є сукупність елементів 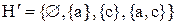 , що може розглядатися як інтервал
, що може розглядатися як інтервал 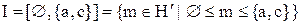 , обмежений найменшим елементом
, обмежений найменшим елементом 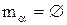 і найбільшим елементом
і найбільшим елементом 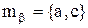 . Нульовий і одиничний елементи в структурі
. Нульовий і одиничний елементи в структурі 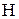 – це
– це 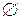 й
й 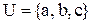 відповідно. Прикладом додаткових елементів у структурі
відповідно. Прикладом додаткових елементів у структурі 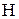 можуть служити
можуть служити  й
й  , оскільки
, оскільки 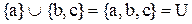 ,
, 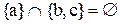 .
.
Серед структур виділяють спеціальні типи, найбільш затребувані на практиці. Це дедекиндові й дистрибутивні структури.
6.2 Дедекиндові (модулярні) структури
Визначення 6.10.Структура називається дедекиндовою (модулярною) тоді й тільки тоді, коли вона має властивість дедекиндовості(модулярності), тобто умові
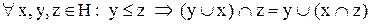 . (6.3)
. (6.3)
Критерій дедекиндовості структури:структура 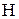 дедекиндова тоді й тільки тоді, коли вона не містить підрешітки виду
дедекиндова тоді й тільки тоді, коли вона не містить підрешітки виду 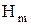 (або ізоморфної їй структури), що містить елемент нульової висоти (1), два елементи одиничної висоти (2,3) і по одному елементу, висота яких 2 і 3 (рис. 6.3).
(або ізоморфної їй структури), що містить елемент нульової висоти (1), два елементи одиничної висоти (2,3) і по одному елементу, висота яких 2 і 3 (рис. 6.3).
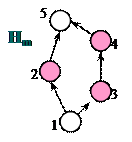
Рис. 6.3. Структура 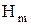 із критерію дедекиндовості
із критерію дедекиндовості
У структурі 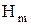 існують елементи, для яких умова дедекиндовості не виконана, а саме:
існують елементи, для яких умова дедекиндовості не виконана, а саме: 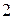 ,
, 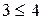 . Перевіримо це:
. Перевіримо це:
6.3 Дистрибутивні структури
Визначення 6.11. Структура 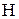 називається дистрибутивною, якщо вона задовольняє властивості дистрибутивності, тобто якщо для будь-яких трьох її елементів
називається дистрибутивною, якщо вона задовольняє властивості дистрибутивності, тобто якщо для будь-яких трьох її елементів  виконані тотожності:
виконані тотожності:
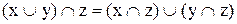 ,
, 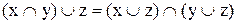 . (6.4)
. (6.4)
Критерій дистрибутивності структури:структура 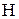 дистрибутивна тоді й тільки тоді, коли вона дедекиндова й не містить підструктури виду
дистрибутивна тоді й тільки тоді, коли вона дедекиндова й не містить підструктури виду 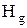 (або ізоморфної їй структури), що містить три ланцюги довжини 2 та складаються з одного елемента нульової висоти, трьох елементів одиничної висоти, одного елемента висоти 2 (рис. 6.4), тобто
(або ізоморфної їй структури), що містить три ланцюги довжини 2 та складаються з одного елемента нульової висоти, трьох елементів одиничної висоти, одного елемента висоти 2 (рис. 6.4), тобто 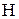 дистрибутивна
дистрибутивна 
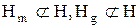 .
.
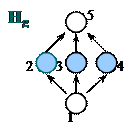
Рис. 6.4. Структура 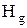 із критерію дистрибутивності
із критерію дистрибутивності
У структурі 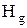 існують елементи, для яких властивість дистрибутивності не виконується
існують елементи, для яких властивість дистрибутивності не виконується 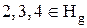 :
:
6.4 Ізоморфізм множин
Визначення 6.12.Множини  й
й 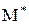 ізоморфні якщо існує взаємо-однозначна відповідність
ізоморфні якщо існує взаємо-однозначна відповідність 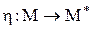 і зворотна відповідність
і зворотна відповідність 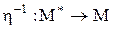 такі, що
такі, що
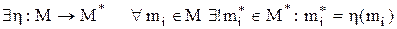 ;
;
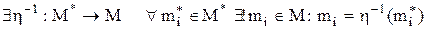 .
.
Визначення 6.13.Упорядковані множини  й
й 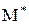 ізоморфні якщо між ними існує ізоморфізм, що зберігає порядок, тобто
ізоморфні якщо між ними існує ізоморфізм, що зберігає порядок, тобто
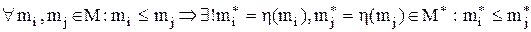 ,
,
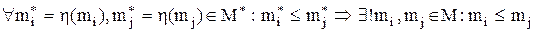 ;
;
інакше, ізоморфізм двох упорядкованих множин  і
і 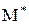 спостерігається при взаємо-однозначній відповідності
спостерігається при взаємо-однозначній відповідності 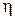 між
між  і
і 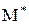 , коли з порівнянності прообразів
, коли з порівнянності прообразів 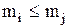 випливає порівнянність їхніх образів
випливає порівнянність їхніх образів  і навпаки: із
і навпаки: із  треба
треба 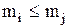 .
.
Приклад 6.4.Будь-які дві алгебри, утворені множинами 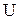 й
й 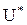 однакової потужності, ізоморфні (операції однакові, а відображення – взаємо-однозначна відповідність множин-носіїв).
однакової потужності, ізоморфні (операції однакові, а відображення – взаємо-однозначна відповідність множин-носіїв).
Поняття ізоморфізму є одним з важливих у математиці. Його сутність можна виразити таким чином: якщо алгебри 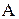 й
й 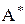 ізоморфні, то елементи й операції в алгебрі
ізоморфні, то елементи й операції в алгебрі 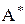 можна перейменувати так, що
можна перейменувати так, що 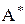 співпадає з
співпадає з 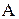 .
.
Будь-яке еквівалентне співвідношення в довільній алгебрі зберігається й у будь-якій ізоморфній їй алгебрі, що дозволяє автоматично поширювати такі співвідношення у вихідній алгебрі на всі ізоморфні їй алгебри. Це дає можливість розглядати об'єкти з точністю до ізоморфізму, тобто розглядати тільки ті властивості об'єктів, які зберігаються при ізоморфізмі. Зокрема, ізоморфізм зберігає такі властивості операцій як асоциативність, комутативність, дистрибутивність.
6.5 Контрольні питання
1. Як визначається структура?
2. Які закони визначають структуру як булеву алгебру?
3. Як формулюється властивість дедекиндовості структури?
4. Як формулюється критерій дедекиндовості структури?
5. Як визначається структура, на якій заснований критерій дедекиндовості?
6. Як визначається властивість дистрибутивності структури?
7. Як формулюється критерій дистрибутивності структури?
8. Які структури використовуються в критерії дистрибутивності?
9. Що називається інтервалом?
10. Які елементи є додатковими в структурі?
11. Які елементи є структурними нулем і одиницею?
12. Які елементи називаються зв'язаними в структурі?
13. Що являє собою структура як алгебраїчна система?
14. Як визначаються супремум та інфімум для пари порівнянних елементів?
15. Що називається ізоморфізмом множин?
16. Чим характеризується ізоморфізм упорядкованих множин?
17. Чим визначається ізоморфізм алгебр?
9. Основні поняття булевої алгебри
9.1 Логічні операції й логічні функції
Визначення 9.1. Логічна (булева) змінна – така величина 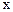 , що може приймати тільки два значення (нуль або одиниця / неправда або істина):
, що може приймати тільки два значення (нуль або одиниця / неправда або істина): 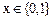 .
.
Визначення 9.2. Логічна (булева або функція алгебри логіки - ФАЛ) є функція від 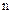 булевих змінних, що приймає значення 0 або 1:
булевих змінних, що приймає значення 0 або 1:
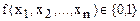 .
.
Змінні булевої функції утворюють набори з нулів і одиниць. Такі набори називаються двійковими й розглядаються як кінцеві впорядковані послідовності, на яких задана булева функція.
Булева функція від n змінних  визначена на
визначена на 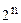 двійкових наборах.
двійкових наборах.
Перехід від десяткової до двійкової системи числення здійснюється відомим способом шляхом розподілу числа з десяткової системи на два. Наприклад, числу 6 у десятковій системі відповідає (1,1,0) у двійковій: 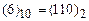 .
.
Кожному двійковому набору відповідає його десятковий еквівалент або порядковий номер (табл. 9.1-9.3).
Таблиця 9.1
Двійкові набори для булевої
функції від двох змінних 
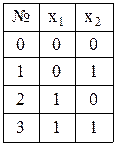
Таблиця 9.2
Двійкові набори для булевої функції від трьох змінних 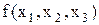

Таблиця 9.3
Двійкові набори для булевої
функції від чотирьох змінних 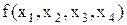
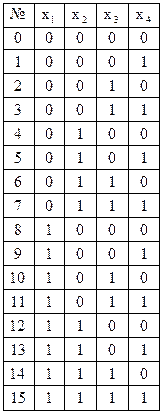
В булевій алгебрі мають місце основні логічні операції – інверсія, кон’юнкція, диз’юнкція, а також імплікація, еквівалентність, сума за модулем два (табл. 9.4).
Таблиця 9.4
Логічні операції
| Назва
| Позначення
| Читання
|
| Диз’юнкція (логічне додавання)
| 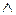 (+) (+)
| x АБО y
|
| Кон’юнкція (логічне множення)
| 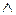 (&, •) (&, •)
| x И y
|
| Інверсія (заперечення)
| – ()
| НЕ x
|
| Імплікація
| 
| x ТЯГНЕ y
|
| Еквівалентність
| ~
| x еквівалентно y
|
| Сума за модулем 2
(виключне АБО чи XOR)
| 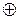
| x сума за модулем 2 y
|
Як і в арифметичному множенні, символ кон’юнкції часто опускається:  або
або 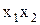 .
.
Кожній логічній операції відповідає логічна функція з однойменною назвою. Оскільки логічні операції є бінарними, крім інверсії, яка є унарною, для їхнього завдання необхідні дві змінні, тобто кожна функція повинна бути визначена на 4-х двійкових наборах. Логічні функції задаються за допомогою таблиць істинності, які є правилами їхнього обчислення (табл. 9.5).
Таблиця 9.5
Таблиці істинності для елементарних булевих функцій
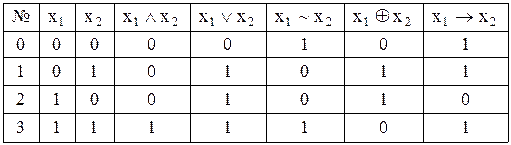
З табл. 9.5 видно, що:
1) Кон’юнкція приймає нульове значення, якщо серед співмножників є хоча б один нуль, і єдине одиничне значення – на наборі з одиниць. Цей підхід можна поширити на добуток 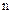 змінних:
змінних:
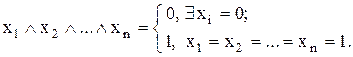 (9.1)
(9.1)
2) Диз’юнкція приймає єдине нульове значення, якщо всі доданки дорівнюють нулю, і одиничне значення, якщо серед доданків є хоча б одна одиниця, тобто для функції від 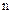 змінних вірно наступне:
змінних вірно наступне:
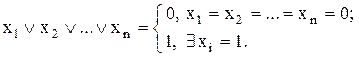 (9.2)
(9.2)
3) Два однакових компоненти еквіваленти, а два різних – ні.
4) Сума за модулем два обертається на нуль, якщо доданки – два однакових компоненти, і дорівнює одиниці – при додаванні двох різних компонентів.
5) Функція імплікація приймає єдине нульове значення, коли 1 тягне (спричиняє) 0.
6) Сума за модулем два та еквівалентність – взаємно зворотні один одному, тобто  ,
, 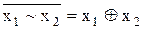 .
.
Функції 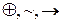 можуть бути представлені через операції
можуть бути представлені через операції 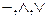 за допомогою формул переходу:
за допомогою формул переходу:
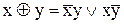 , (9.3)
, (9.3)
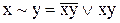 , (9.4)
, (9.4)
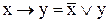 . (9.5)
. (9.5)
Пріоритет виконання операцій визначається дужками в логічному виразі, яким представлена функція. Якщо не зазначено інакше, операції виконуються в такому порядку: 1) інверсія, 2) кон’юнкція, 3) диз’юнкція.
За допомогою таблиць істинності можна знаходити значення булевих функцій. При цьому треба логічний вираз, яким задана функція, розбити на елементарні операції (унарну та бінарні), і потім обчислити їх послідовно відповідно до порядку їхнього виконання.
Приклад 9.1.Скласти таблицю істинності для функції
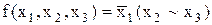 .
.
Розв’язок. Потрібно скласти таблицю істинності для функції від 3 змінних. Вона визначена на стандартних 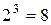 двійкових наборах (див. табл. 9.2). Порядок обчислення функції встановлений дужками й буде таким:
двійкових наборах (див. табл. 9.2). Порядок обчислення функції встановлений дужками й буде таким: 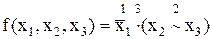 (табл. 9.6).
(табл. 9.6).
Таблиця 9.6
Обчислення функції 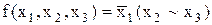

9.2 Закони й тотожності булевої алгебри
Для булевої алгебри мають місце наступні закони (з точністю до позначення операцій такі ж, що й для алгебри множин).
1. Комутативність:
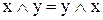 ,
, 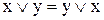 . (9.6)
. (9.6)
2. Асоціативність:
 ,
, 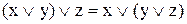 . (9.7)
. (9.7)
3. Дистрибутивність (розподільний закон):
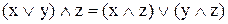 ,
, 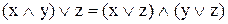 . (9.8)
. (9.8)
4. Ідемпотентність (повторення, тавтологія):
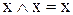 ,
, 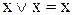 . (9.9)
. (9.9)
5. Операції з константами (як константи виступають елементи 0 і 1):
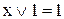 ,
, 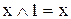 ,
,  ,
, 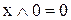 . (9.10)
. (9.10)
6. Закон виключеного третього:
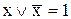 . (9.11)
. (9.11)
7. Закон протиріччя:
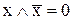 . (9.12)
. (9.12)
8. Інволюція (подвійне заперечення):
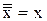 . (9.13)
. (9.13)
9. Закон Де Моргана:
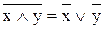 ,
, 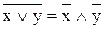 . (9.14)
. (9.14)
10. Елімінація (поглинання):
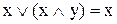 ,
,  . (9.15)
. (9.15)
11. Склеювання:
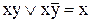 ,
, 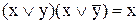 . (9.16)
. (9.16)
12. Закони Порецького (Блейка-Порецького):
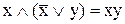 ,
, 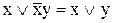 . (9.17)
. (9.17)
9.3 Доведення законів булевої алгебри
Справедливість законів може бути встановлена за допомогою таблиць істинності. Ідея доказу полягає в наступному. У загальній таблиці істинності послідовно виконуються обчислення для лівої, а потім для правої частин рівності. Отримані стовпці значень повинні бути однаковими.
Приклад 9.2. Довести дистрибутивний закон 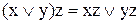 за допомогою таблиці істинності.
за допомогою таблиці істинності.
Доказ. Ліва й права частини дистрибутивного закону містять три змінні. Слід скласти таблицю істинності, що включає 8 двійкових наборів (табл. 9.7).
Таблиця 9.7
Доказ дистрибутивного закону 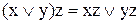
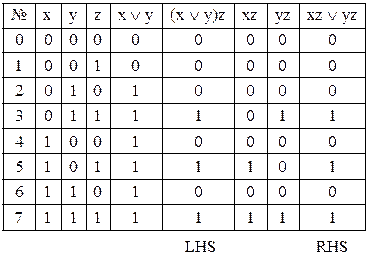
З таблиці істинності видно, що стовпці значень для лівої (LHS) і правої (RHS) частин рівностей збігаються.
Приклад 9.3. Використовуючи дистрибутивний закон, установити справедливість закону Блейка-Порецького 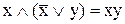 аналітично.
аналітично.
Доказ. Щоб розкрити дужки в правій частині рівності, необхідно послідовно застосувати дистрибутивний закон, закон протиріччя та дії з константами:
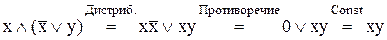 ,
,
що й було потрібно довести.
9.4 Контрольні питання
1. Які змінні є булевими?
2. Як визначається булева функція?
3. Скільки двійкових наборів містить булева функція від n змінних?
4. Які існують основні логічні операції? Як вони позначаються?
5. Як задаються логічні функції за допомогою таблиць істинності?
6. На яких двійкових наборах кон’юнкція обертається на нуль?
7. На яких двійкових наборах диз’юнкція дорівнює одиниці?
8. Чому дорівнює сума за модулем два n змінних 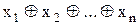 ?
?
9. Як установлюється пріоритет логічних операцій?
10. Як формулюються закони булевої алгебри?
11. У якому алфавіті визначається алгебра логіки?
12. Чому дорівнює: 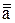 ,
, 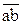 ,
, 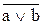 ?
?
13. Скільки рядків містить таблиця істинності функції f(a,b,c)?
14. Скільки рядків містить таблиця істинності функції f(a,b,c,d)?
15. За якою формулою визначається зв'язок суми за модулем два з інверсією, кон’юнкцією, диз’юнкцією?
16. За якою формулою встановлюється зв’язок еквівалентності з інверсією, кон’юнкцією, диз’юнкцією?
17. Які логічні операції є бінарними?
18. На якому двійковому наборі функція імплікація звертається в нуль?
19. Чому дорівнює вираз  ?
?
20. Чому дорівнює вираз 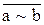 ?
?
21. За якою формулою встановлюється зв’язок імплікації з інверсією та диз’юнкцією?
10 Диз’юнктивні та кон’юнктивні нормальні форми (ДНФ і КНФ). Досконалі ДНФ і КНФ (ДДНФ і ДКНФ)
ДНФ КНФ, ДДНФ і ДКНФ є різними формами зображення булевих функцій і відіграють особливу роль в алгебрі логіки та її додатків.
У загальному виді двійковий набір можна представити як послідовність  , де кожний компонент є нуль або одиниця, тобто
, де кожний компонент є нуль або одиниця, тобто 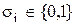 .
.
10.1 ДНФ і КНФ
Визначення 10.1. Змінна або її інверсія називається первинним термом імає узагальнене позначення:
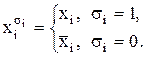 (10.1)
(10.1)
Визначення 10.2.Формула виду
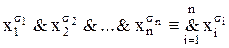 , (10.2)
, (10.2)
де  – двійковий набір, називається елементарною кон’юнкцією.
– двійковий набір, називається елементарною кон’юнкцією.
Визначення 10.3. Диз’юнктивною нормальною формою (ДНФ) називається диз’юнкція елементарних кон’юнкцій: 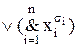 .
.
Визначення 10.4. Формула виду
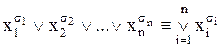 (10.3)
(10.3)
називається елементарною диз’юнкцією.
Визначення 10.5. Кон’юнктивною нормальною формою (КНФ) називається кон’юнкція елементарних диз’юнкцій: 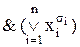 .
.
Булеву функцію, представлену довільним логічним виразом, можна привести до ДНФ і КНФ шляхом застосування еквівалентних перетворень на основі законів булевої алгебри.
Приклад 10.1.Привести функцію 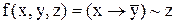 до ДНФ і КНФ.
до ДНФ і КНФ.
Розв’язок. 1) Щоб привести функцію до ДНФ, необхідно послідовно застосувати визначення операцій імплікації та еквівалентності, закони Де Моргана та дистрибутивності):
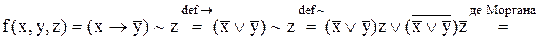
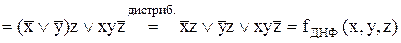 .
.
2) застосування дистрибутивного закону до останнього виразу дає КНФ:
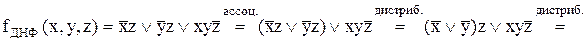
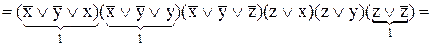
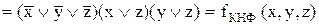 .
.
10.2 ДДНФ і ДКНФ
Визначення 10.6.Досконалою ДНФ (ДДНФ) називається ДНФ, у якій немає рівних елементарних кон’юнкцій і всі елементарні кон’юнкції містять ті самі змінні, від яких залежить функція, причому кожну змінну – тільки один раз (з урахуванням входження під знаком інверсії).
Визначення 10.7.Досконала КНФ (ДКНФ) визначається як така КНФ, у якій немає однакових співмножників; всі співмножники містять ті самі змінні, причому кожну змінну, від яких залежить функція, – тільки один раз.
Для кожної відмінної від нуля булевої функції  можна побудувати реалізацію у вигляді ДДНФ:
можна побудувати реалізацію у вигляді ДДНФ:
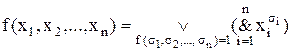 , (10.4)
, (10.4)
де диз’юнкція береться по тим двійковим наборам, на яких функція приймає одиничні значення 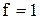 .
.
Кожна функція алгебри логіки  реалізується наступною ДКНФ:
реалізується наступною ДКНФ:
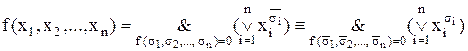 . (10.5)
. (10.5)


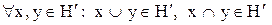 .
.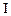 називається підструктури
називається підструктури 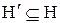 з найменшим елементом
з найменшим елементом 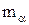 і найбільшим елементом
і найбільшим елементом  :
:  .
.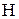 зі структурними нулем і одиницею два елементи
зі структурними нулем і одиницею два елементи  ,
,  .
.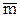 , додатковий до елемента
, додатковий до елемента 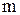 , називається доповненням елемента
, називається доповненням елемента 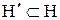 є сукупність елементів
є сукупність елементів 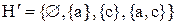 , що може розглядатися як інтервал
, що може розглядатися як інтервал 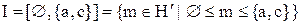 , обмежений найменшим елементом
, обмежений найменшим елементом 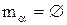 і найбільшим елементом
і найбільшим елементом 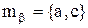 . Нульовий і одиничний елементи в структурі
. Нульовий і одиничний елементи в структурі 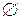 й
й 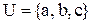 відповідно. Прикладом додаткових елементів у структурі
відповідно. Прикладом додаткових елементів у структурі  й
й  , оскільки
, оскільки 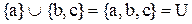 ,
, 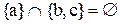 .
.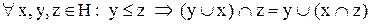 . (6.3)
. (6.3)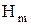 (або ізоморфної їй структури), що містить елемент нульової висоти (1), два елементи одиничної висоти (2,3) і по одному елементу, висота яких 2 і 3 (рис. 6.3).
(або ізоморфної їй структури), що містить елемент нульової висоти (1), два елементи одиничної висоти (2,3) і по одному елементу, висота яких 2 і 3 (рис. 6.3).
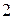 ,
, 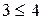 . Перевіримо це:
. Перевіримо це: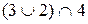
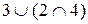
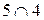
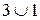
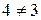
 виконані тотожності:
виконані тотожності: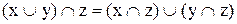 ,
, 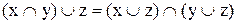 . (6.4)
. (6.4)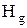 (або ізоморфної їй структури), що містить три ланцюги довжини 2 та складаються з одного елемента нульової висоти, трьох елементів одиничної висоти, одного елемента висоти 2 (рис. 6.4), тобто
(або ізоморфної їй структури), що містить три ланцюги довжини 2 та складаються з одного елемента нульової висоти, трьох елементів одиничної висоти, одного елемента висоти 2 (рис. 6.4), тобто 
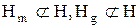 .
.
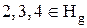 :
: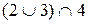
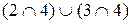
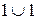
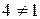
 й
й 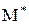 ізоморфні якщо існує взаємо-однозначна відповідність
ізоморфні якщо існує взаємо-однозначна відповідність 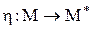 і зворотна відповідність
і зворотна відповідність 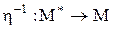 такі, що
такі, що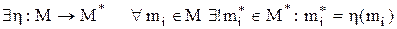 ;
;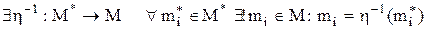 .
.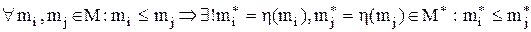 ,
,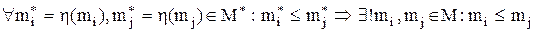 ;
;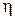 між
між 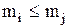 випливає порівнянність їхніх образів
випливає порівнянність їхніх образів  і навпаки: із
і навпаки: із 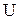 й
й 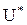 однакової потужності, ізоморфні (операції однакові, а відображення – взаємо-однозначна відповідність множин-носіїв).
однакової потужності, ізоморфні (операції однакові, а відображення – взаємо-однозначна відповідність множин-носіїв).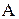 й
й 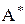 ізоморфні, то елементи й операції в алгебрі
ізоморфні, то елементи й операції в алгебрі 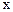 , що може приймати тільки два значення (нуль або одиниця / неправда або істина):
, що може приймати тільки два значення (нуль або одиниця / неправда або істина): 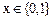 .
.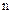 булевих змінних, що приймає значення 0 або 1:
булевих змінних, що приймає значення 0 або 1: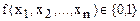 .
. визначена на
визначена на 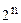 двійкових наборах.
двійкових наборах.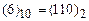 .
.
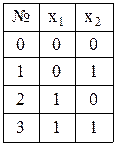
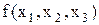

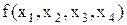
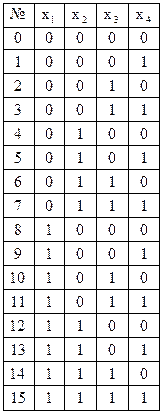
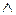 (+)
(+)

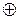
 або
або 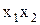 .
.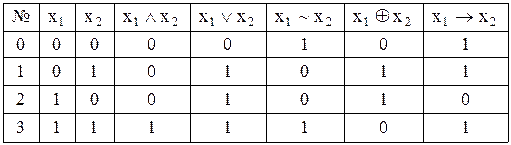
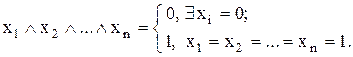 (9.1)
(9.1)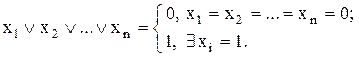 (9.2)
(9.2) ,
, 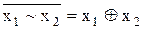 .
.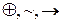 можуть бути представлені через операції
можуть бути представлені через операції 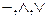 за допомогою формул переходу:
за допомогою формул переходу: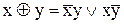 , (9.3)
, (9.3)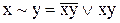 , (9.4)
, (9.4)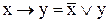 . (9.5)
. (9.5)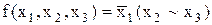 .
.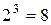 двійкових наборах (див. табл. 9.2). Порядок обчислення функції встановлений дужками й буде таким:
двійкових наборах (див. табл. 9.2). Порядок обчислення функції встановлений дужками й буде таким: 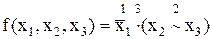 (табл. 9.6).
(табл. 9.6).
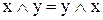 ,
, 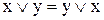 . (9.6)
. (9.6) ,
, 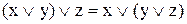 . (9.7)
. (9.7)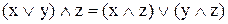 ,
, 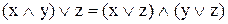 . (9.8)
. (9.8)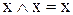 ,
, 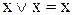 . (9.9)
. (9.9)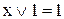 ,
, 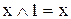 ,
,  ,
, 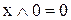 . (9.10)
. (9.10)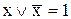 . (9.11)
. (9.11)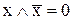 . (9.12)
. (9.12)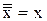 . (9.13)
. (9.13)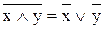 ,
, 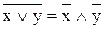 . (9.14)
. (9.14)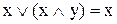 ,
,  . (9.15)
. (9.15)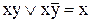 ,
, 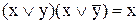 . (9.16)
. (9.16)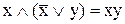 ,
, 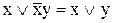 . (9.17)
. (9.17)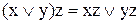 за допомогою таблиці істинності.
за допомогою таблиці істинності.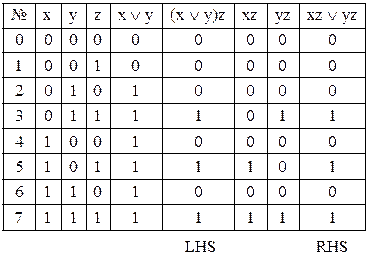
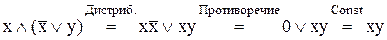 ,
,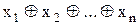 ?
?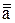 ,
, 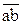 ,
, 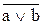 ?
? ?
?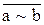 ?
? , де кожний компонент є нуль або одиниця, тобто
, де кожний компонент є нуль або одиниця, тобто 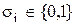 .
.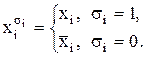 (10.1)
(10.1)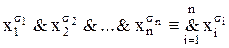 , (10.2)
, (10.2)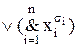 .
.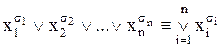 (10.3)
(10.3)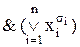 .
.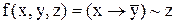 до ДНФ і КНФ.
до ДНФ і КНФ.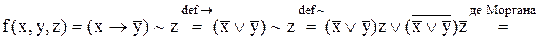
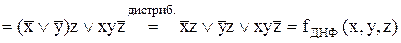 .
.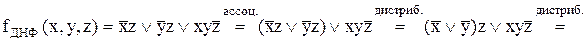
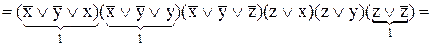
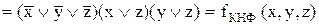 .
. можна побудувати реалізацію у вигляді ДДНФ:
можна побудувати реалізацію у вигляді ДДНФ: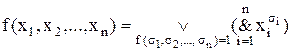 , (10.4)
, (10.4)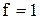 .
. реалізується наступною ДКНФ:
реалізується наступною ДКНФ: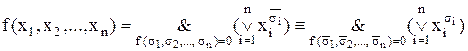 . (10.5)
. (10.5)