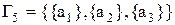 – сама дрібна (мінімальна) розбивка, що складається з одноелементних підмножин множини
– сама дрібна (мінімальна) розбивка, що складається з одноелементних підмножин множини 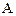 , індекс розбивки дорівнює 3.
, індекс розбивки дорівнює 3.
Приклад 4.10. Максимальна розбивка індексу 1 завжди містить одну єдину множину 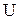 , на якій воно розглядається:
, на якій воно розглядається: 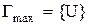 – тут усього один клас, він еквівалентний U.
– тут усього один клас, він еквівалентний U.
Приклад 4.11. Множина всіх одноелементних підмножин становить саму дрібну розбивку, індекс якої співпадає з потужністю вихідної множини: 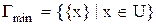 .
.
Розглянемо схему розбивки множини на класи еквівалентності. Нехай на кінцевій множині  задане відношення еквівалентності
задане відношення еквівалентності 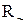 . Здійснимо наступну побудову:
. Здійснимо наступну побудову:
– виберемо елемент 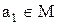 і утворимо підмножину (клас)
і утворимо підмножину (клас) 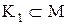 , що складається з елемента
, що складається з елемента 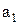 та всіх елементів, еквівалентних йому:
та всіх елементів, еквівалентних йому:
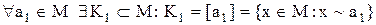 ;
;
– виберемо елемент 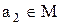 ,
, 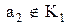 і утворимо підмножину (клас еквівалентності)
і утворимо підмножину (клас еквівалентності) 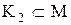 елемента
елемента 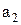 , що складається з
, що складається з 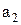 і всіх елементів, еквівалентних йому:
і всіх елементів, еквівалентних йому:
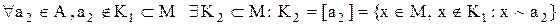 ;
;
і т.п.
У результаті такої побудови породжується система класів 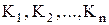 така, що будь-який елемент із множини
така, що будь-який елемент із множини  входить хоча б в один клас, тобто
входить хоча б в один клас, тобто 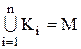 .
.
Дана система має наступні властивості:
1) утворює розбивку, тобто класи попарно не перетинаються: 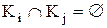 ;
;
2) будь-які два елементи з одного класу еквівалентні:  ;
;
3) будь-які два елементи з різних класів не еквівалентні:
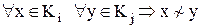 .
.
Побудована розбивка (система класів) називається системою класів еквівалентності за відношенням 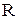 .
.
Класи еквівалентності мають наступні властивості:
1) Елемент належить своєму класу еквівалентності: 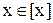 .
.
2) Якщо елемент 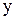 належить класу еквівалентності елемента
належить класу еквівалентності елемента 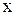 , то класи еквівалентності елементів
, то класи еквівалентності елементів 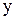 і
і 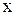 співпадають:
співпадають: 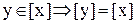 .
.
3) Якщо класи еквівалентності перетинаються, то вони співпадають:
 ;
;
нерівні (різні) класи еквівалентності не перетинаються:
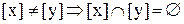 .
.
Таким чином, класи еквівалентності або не перетинаються, або співпадають:  .
.
4) Об'єднанням класів еквівалентності є вся множина  :
:  .
.
Отже, класи еквівалентності утворюють розбивку множини. Матрицю бінарного відношення еквівалентності можна зобразити у блочно-діагональному вигляді (рис. 4.10), де кожна підматриця, що складається з одиниць, відповідає класу еквівалентності.
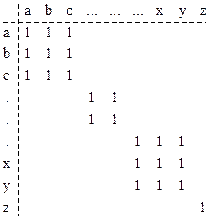
Рис. 4.10. Матриця бінарного відношення еквівалентності
З формальної точки зору модель є фактор-множина елементів об'єкта, що моделюється, щодо деякого відношення еквівалентності, заданого на вихідній системі. Поняття “відношення еквівалентності”, “ фактор-множина”, “класи еквівалентності” використовуються при побудові математичної моделі деякої реально функціонуючої складної системи. При дослідженні виникає завдання вибору істотних властивостей, деталей, ознак об'єкта, який моделюється. Відношення еквівалентності, з одного боку, ототожнює другорядні, несуттєві ознаки й властивості, з іншого боку – виділяє як представників класів еквівалентності основні властивості.
4.4 Контрольні питання
1. Яке відношення називається бінарним?
2. Якими способами можна задати бінарне відношення?
3. Як визначається матриця суміжності?
4. Чим визначається розмір матриці суміжності?
5. Що являє собою граф бінарного відношення?
6. Які властивості мають бінарні відношення?
7. Як визначається властивість рефлексивності?
8. Чим характеризується матриця суміжності рефлексивного бінарного відношення?
9. Які характерні ознаки має граф рефлексивного відношення?
10. Як визначається властивість симетричності?
5. Бінарне відношення порядку
5.1 Упорядковані множини. Бінарне відношення порядку
Визначення 5.1. Упорядкованою називається множина  із заданим відношенням порядку
із заданим відношенням порядку 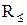 :
: 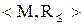 .
.
Символ 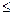 означає порівнянність елементів множини
означає порівнянність елементів множини  :
: 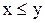 .
.
Визначення 5.2. Бінарним відношенням порядку (упорядкованості) називається рефлексивне, антисиметричне й транзитивне відношення:
1) Рефлексивність означає, що кожний елемент порівняний сам із собою:
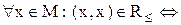
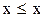 ; (5.1)
; (5.1)
2) Антисиметричність означає, що якщо елемент 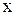 порівняний з елементом
порівняний з елементом 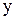 , а
, а 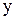 порівняний з
порівняний з 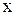 , то
, то 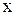 та
та 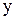 співпадають:
співпадають: 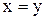 ;
;
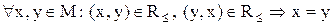 , тобто
, тобто  ; (5.2)
; (5.2)
3) Транзитивність: якщо елемент 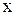 порівняний із елементом
порівняний із елементом 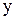 , а
, а 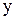 порівняний із
порівняний із 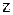 , то
, то 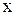 порівняний із
порівняний із 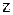 :
:
 ,
,
тобто  . (5.3)
. (5.3)
5.2 Типи порядку (лінійний, частковий, передпорядок)
Визначення 5.3. Бінарне відношення, що має властивості антирефлексивності, антисиметричності й транзитивності, називається відношенням строгої впорядкованості й позначається 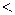 .
.
Визначення 5.4.Бінарне відношення, що має властивості рефлексивності й транзитивності, називається відношенням передпорядку.
Визначення 5.5.Множина називається лінійно (повністю) упорядкованою, якщо будь-які два його елементи порівнянні, тобто, 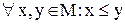 або
або 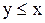 , інакше – множина є частково впорядкованою (існують непорівняні між собою елементи).
, інакше – множина є частково впорядкованою (існують непорівняні між собою елементи).
Приклад 5.1.На множині дійсних чисел 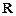 відношення порядку встановлюється за принципом порівнянності ”менше або дорівнює” (рис. 5.1):
відношення порядку встановлюється за принципом порівнянності ”менше або дорівнює” (рис. 5.1): 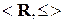 . Виконання аксіом 1-3 очевидно.
. Виконання аксіом 1-3 очевидно.

Рис. 5.1. Відношення лінійного порядку на множині дійсних чисел
Приклад 5.2. Для множини  елементи булеану
елементи булеану 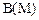 упорядковуються за включенням та утворюють частково впорядковану множину
упорядковуються за включенням та утворюють частково впорядковану множину 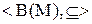 , що зображено діаграмою (рис. 5.2).
, що зображено діаграмою (рис. 5.2).
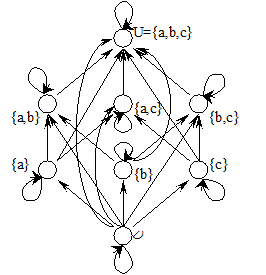
Рис. 5.2. Частково впорядкована множина 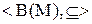 із приклада 5.2
із приклада 5.2
Частково впорядковані множини зображуються у вигляді графів – діаграм Хасе 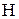 , – у яких вилучені всі петлі та всі транзитивно замикаючі дуги, і позначаються
, – у яких вилучені всі петлі та всі транзитивно замикаючі дуги, і позначаються 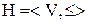 . Діаграма Хасе відома у генеалогії з XIX ст. і використовувалася при завданні споріднення.
. Діаграма Хасе відома у генеалогії з XIX ст. і використовувалася при завданні споріднення.
Таким чином, діаграма Хасе являє собою граф, вершини якого є елементи множини (домену або класу), а з'єднуючі їх лінії (ребра або дуги) установлюють зв'язку між елементами безлічі (домена або класу), що інтерпретуються як відношення часткового порядку.
Дана теоретична концепція реалізується в мовах об’єктно-орієнтованого програмування, зокрема, C#.
Приклад 5.3. Видалення з діаграми (див. рис. 5.2), що ілюструє включення елементів булеана триелементної множини один до одного, всіх петель і всіх транзитивно замикаючих дуг дає діаграму Хасе, що також зображує частково впорядковану множину (рис. 5.3).
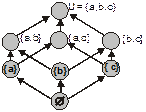
Рис. 5.3. Діаграма Хасе для множини 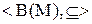 із приклада 5.2
із приклада 5.2
Приклад 5.4. Коди можна розглядати як деякі геометричні просторові фігури. Тріаду можна зобразити у вигляді одиничного куба, що має координати вершин, які відповідають двійковим символам (рис. 5.4). Вершини одиничного куба відповідають уявленню чисел 0-8 у двійковій системі числення.

Рис. 5.4. Геометричне зображення кодів у вигляді діаграми Хасе
Визначення 5.6. Елемент 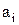 покриває елемент
покриває елемент 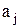 , якщо
, якщо
 та
та 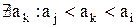
При цьому 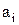 називається старшим елементом.
називається старшим елементом.
Можна розглядати відношення покриття в упорядкованій множині.
Визначення 5.7. Найменшим (найбільшим) елементом множини  часткового порядку називається елемент
часткового порядку називається елемент 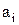 якщо
якщо 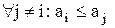 (
( 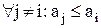 ). Найменший (найбільший) елемент називають мінорантою (мажорантою).
). Найменший (найбільший) елемент називають мінорантою (мажорантою).
Визначення 5.8. Нехай 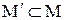 . Мінімальний (максимальний) елемент із множини мажорант (мінорант) називається верхньою (нижньою) гранню.
. Мінімальний (максимальний) елемент із множини мажорант (мінорант) називається верхньою (нижньою) гранню.
Визначення 5.9. Нехай 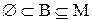 . Найменший (найбільший) елемент множини всіх верхніх (нижніх) граней
. Найменший (найбільший) елемент множини всіх верхніх (нижніх) граней 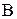 називається точною верхньою (нижньою) гранню множини
називається точною верхньою (нижньою) гранню множини 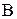 й позначається
й позначається  (
( 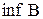 ).
).
В упорядкованому сімействі множини  порожня множина є нульовим елементом, тобто
порожня множина є нульовим елементом, тобто 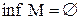 ; універсум
; універсум  – одиничним елементом, тобто
– одиничним елементом, тобто 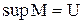 .
.
Приклад 5.5. Нехай множина 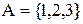 частково впорядкована відношенням включення
частково впорядкована відношенням включення 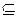 :
:  (рис. 5.5). Елемент
(рис. 5.5). Елемент 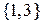 покриває елемент
покриває елемент  , тобто
, тобто 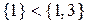 , отже,
, отже, 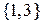 є старшим у порівнянні з
є старшим у порівнянні з  . На множині
. На множині 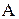 розглядаються дві підмножини:
розглядаються дві підмножини: 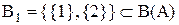 ;
; 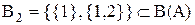 . Множина верхніх граней для
. Множина верхніх граней для 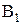 визначається як сукупність
визначається як сукупність 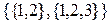 , нижня грань –
, нижня грань –  . Супремум
. Супремум 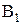 є найменша з верхніх граней:
є найменша з верхніх граней: 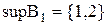 , інфімум
, інфімум 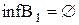 , при цьому жодна із зазначених граней не належить до B1. Mножина верхніх граней
, при цьому жодна із зазначених граней не належить до B1. Mножина верхніх граней  –
– 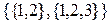 , а множина нижніх граней
, а множина нижніх граней  є сукупність елементів
є сукупність елементів 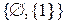 . Тоді
. Тоді 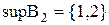 ,
, 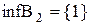 , тобто обидві точні грані належать множині
, тобто обидві точні грані належать множині  .
.
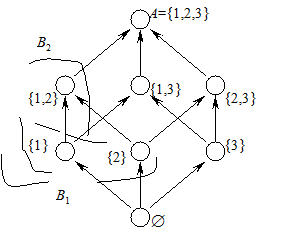
Рис. 5.5. Частково впорядкована множина 
Теорема 5.1. Упорядкована множина М містить не більше одного найбільшого (найменшого) елемента.
Доказ. Якщо припустити, що існує більше одного найбільшого (найменшого) елемента, тобто 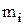 й
й 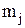 – два найбільших (найменших) елементи, тоді
– два найбільших (найменших) елементи, тоді 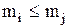 або
або 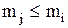 (
( 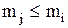 або
або 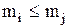 ), отже, в силу антисиметричності одержуємо
), отже, в силу антисиметричності одержуємо 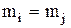 – єдиний найбільший (найменший) елемент. Що й було потрібно довести.
– єдиний найбільший (найменший) елемент. Що й було потрібно довести.
Визначення 5.10. Відношення  (або
(або 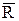 ) називається зворотнім до бінарного відношення
) називається зворотнім до бінарного відношення 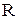 , якщо виконується умова:
, якщо виконується умова:
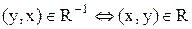 .
.
Принцип подвійності: відношення, зворотне відношенню впорядкованості, є відношенням упорядкованості. Упорядковані множини  й
й 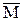 двоїсті, якщо
двоїсті, якщо 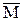 визначено на тім самом носії за допомогою зворотного відношення
визначено на тім самом носії за допомогою зворотного відношення  .
.
Відношення, зворотне до відношення впорядкованості, ілюструється діаграмою, двоїстою до діаграми Хасе.
Приклад 5.6. На триелементній множині 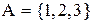 із приклада 5.5 задане зворотне відношення
із приклада 5.5 задане зворотне відношення  , яке можна проілюструвати діаграмою (рис. 5.6).
, яке можна проілюструвати діаграмою (рис. 5.6).

Рис. 5.6. Діаграма, зворотна до діаграми Хасе із приклада 5.5
Визначення 5.11.Ланцюгом 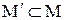 називається підмножина впорядкованої множини. Довжина ланцюга
називається підмножина впорядкованої множини. Довжина ланцюга 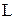 визначається як
визначається як 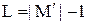 , де
, де 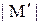 – потужність носія.
– потужність носія.
Приклад 5.7. Підмножина  із приклада 5.5 є ланцюгом у множині
із приклада 5.5 є ланцюгом у множині 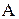 . Довжина
. Довжина  обчислюється відповідно до визначення 5.11 і дорівнює:
обчислюється відповідно до визначення 5.11 і дорівнює:  .
.
Визначення 5.12.Висотою 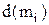 елемента
елемента 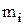 впорядкованої множини
впорядкованої множини  називається максимум довжин ланцюгів
називається максимум довжин ланцюгів 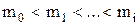 в
в  , для яких
, для яких 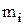 – найбільший елемент,
– найбільший елемент, 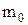 – мінімальний елемент множини
– мінімальний елемент множини  .
.
Приклад 5.8. Висота елемента 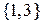 в множині
в множині 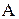 (див. приклад 5.5, рис. 5.5) визначається максимумом довжин ланцюгів
(див. приклад 5.5, рис. 5.5) визначається максимумом довжин ланцюгів 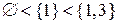 і
і 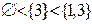 . Оскільки обидві ланцюги мають довжину 2, то висота елемента
. Оскільки обидві ланцюги мають довжину 2, то висота елемента 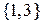 також дорівнює 2:
також дорівнює 2: 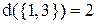 .
.
Визначення 5.13.Довжиною 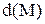 впорядкованої множини
впорядкованої множини  називається максимум довжин ланцюгів в
називається максимум довжин ланцюгів в  або максимум висот
або максимум висот 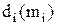 його елементів:
його елементів:
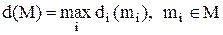 .
.
Приклад 5.9. Довжина множини 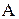 із приклада 5.5, по визначенню 5.13 дорівнює:
із приклада 5.5, по визначенню 5.13 дорівнює:
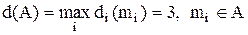 .
.
5.3 Контрольні питання
1. Яке відношення називається відношенням порядку?
2. Які властивості має відношення порядку?
3. Яка множина називається впорядкованою?
4. Чим відрізняється лінійний порядок від часткового?
5. Чим відрізняється строгий порядок від нестрогого?
6. Як формулюється аксіома антисиметричності бінарного відношення?
7. Що являє собою діаграма Хасе?
8. Як визначається покриваємість елементів у частково впорядкованій множині?
9. Які елементи називаються порівнянними в частково впорядкованій множині?
10. Що таке верхня (нижня) грань?
11. Який елемент в упорядкованій множині називається найбільшим (найменшим)?
12. Як визначається супремум та інфімум у частково впорядкованій множині?
13. Яка множина називається ланцюгом?
14. Як визначається довжина ланцюга?
15. Як визначається висота елемента?
16. Як визначається висота частково впорядкованої множини?
17. Який елемент називається старшим?
6 Структури. Алгебраїчні системи. Ізоморфізм
Структура – від латинського: розташування, будова. Щоб визначити структуру, задають відношення, у яких перебувають елементи множини, та аксіоми структури.
Поняття структури відноситься до середини XIX ст. Уперше його ввів німецький математик Дедекинд Рихард Юліус Вільгельм. Термін “структура” належить американському вченому Гаррету Биркгофу із Принстонского університету.
6.1 Структура
Визначення 6.1.Структура – частково впорядкована множина, у якій кожна двоелементна підмножина має одну єдину точну верхню (супремум) і точну нижню (інфімум) грані:
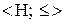 :
: 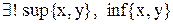 .
.
Визначення 6.2. Структура – це алгебраїчна система 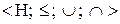 , для елементів якої справедливі закони ідемпотентності, комутативності, поглинання:
, для елементів якої справедливі закони ідемпотентності, комутативності, поглинання:
1)  ;
;
2) 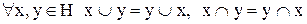 ;
;
3)  ,
,
і будь-які два елементи мають по одній єдиній точній верхній та нижній грані:
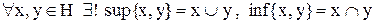 . (6.1)
. (6.1)
Зауваження. Упорядкована система елементів не є структурою, якщо не існують супремум або інфімум; або вони існують, але не є єдиними.
Приклад 6.1.Будь-яка лінійно впорядкована множина 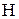 є структурою, причому якщо
є структурою, причому якщо 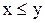 , то
, то  . У якості
. У якості 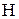 може розглядатися множина дійсних чисел
може розглядатися множина дійсних чисел 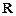 (рис. 6.1).
(рис. 6.1).

Рис. 6.1. Лінійно впорядкована множина як структура
Приклад 6.2. Множина всіх підмножин даної множини (булеан), упорядкована за включенням, із двома бінарними операціями об'єднання й перетинання: 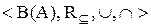 (рис. 6.2).
(рис. 6.2).
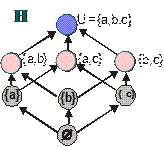
Рис. 6.2. Частково впорядкована множина 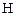 як структура
як структура
Визначення 6.3. Структура 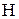 може бути також визначена як універсальна алгебра із двома бінарними операціями об'єднання
може бути також визначена як універсальна алгебра із двома бінарними операціями об'єднання 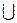 , перетинання
, перетинання 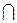 (додавання
(додавання 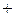 й множення
й множення  ; диз'юнкції
; диз'юнкції 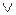 , кон’юнкції
, кон’юнкції 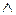 ), що задовольняють властивостям (властивості сформульовані в термінах теоретико-множинних операцій):
), що задовольняють властивостям (властивості сформульовані в термінах теоретико-множинних операцій):
1)  (ідемпотентність);
(ідемпотентність);
2) 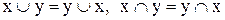 (комутативність);
(комутативність);
3) 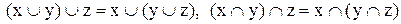 (асоціативність);
(асоціативність);
3) 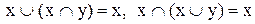 (елімінація)
(елімінація)
і для будь-яких двох елементів виконується умова
 . (6.2)
. (6.2)
Визначення 6.4.Підструктура  є підмножина структури
є підмножина структури 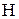 , що разом з кожною парою елементів
, що разом з кожною парою елементів 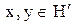 містить також їхнє об'єднання
містить також їхнє об'єднання 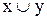 (sup) і перетинання
(sup) і перетинання 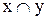 (inf) , тобто
(inf) , тобто


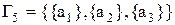 – сама дрібна (мінімальна) розбивка, що складається з одноелементних підмножин множини
– сама дрібна (мінімальна) розбивка, що складається з одноелементних підмножин множини 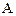 , індекс розбивки дорівнює 3.
, індекс розбивки дорівнює 3.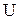 , на якій воно розглядається:
, на якій воно розглядається: 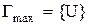 – тут усього один клас, він еквівалентний U.
– тут усього один клас, він еквівалентний U.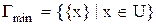 .
. задане відношення еквівалентності
задане відношення еквівалентності 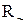 . Здійснимо наступну побудову:
. Здійснимо наступну побудову: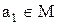 і утворимо підмножину (клас)
і утворимо підмножину (клас) 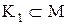 , що складається з елемента
, що складається з елемента 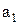 та всіх елементів, еквівалентних йому:
та всіх елементів, еквівалентних йому: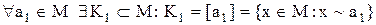 ;
;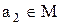 ,
, 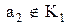 і утворимо підмножину (клас еквівалентності)
і утворимо підмножину (клас еквівалентності) 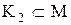 елемента
елемента 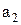 , що складається з
, що складається з 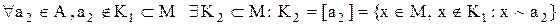 ;
;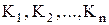 така, що будь-який елемент із множини
така, що будь-який елемент із множини  входить хоча б в один клас, тобто
входить хоча б в один клас, тобто 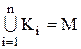 .
.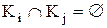 ;
; ;
;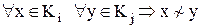 .
.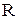 .
.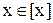 .
.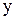 належить класу еквівалентності елемента
належить класу еквівалентності елемента 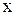 , то класи еквівалентності елементів
, то класи еквівалентності елементів 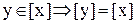 .
. ;
;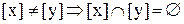 .
. .
. .
.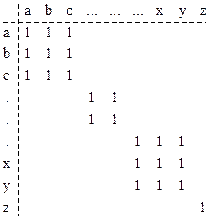
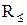 :
: 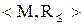 .
.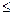 означає порівнянність елементів множини
означає порівнянність елементів множини 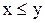 .
.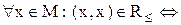
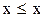 ; (5.1)
; (5.1)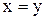 ;
;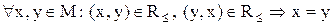 , тобто
, тобто  ; (5.2)
; (5.2)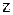 , то
, то  ,
, . (5.3)
. (5.3)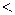 .
.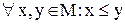 або
або 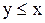 , інакше – множина є частково впорядкованою (існують непорівняні між собою елементи).
, інакше – множина є частково впорядкованою (існують непорівняні між собою елементи).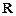 відношення порядку встановлюється за принципом порівнянності ”менше або дорівнює” (рис. 5.1):
відношення порядку встановлюється за принципом порівнянності ”менше або дорівнює” (рис. 5.1): 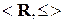 . Виконання аксіом 1-3 очевидно.
. Виконання аксіом 1-3 очевидно.
 елементи булеану
елементи булеану 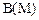 упорядковуються за включенням та утворюють частково впорядковану множину
упорядковуються за включенням та утворюють частково впорядковану множину 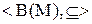 , що зображено діаграмою (рис. 5.2).
, що зображено діаграмою (рис. 5.2).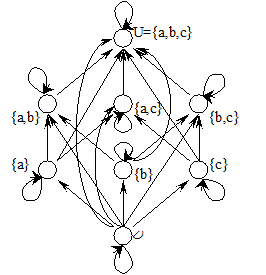
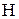 , – у яких вилучені всі петлі та всі транзитивно замикаючі дуги, і позначаються
, – у яких вилучені всі петлі та всі транзитивно замикаючі дуги, і позначаються 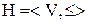 . Діаграма Хасе відома у генеалогії з XIX ст. і використовувалася при завданні споріднення.
. Діаграма Хасе відома у генеалогії з XIX ст. і використовувалася при завданні споріднення.

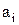 покриває елемент
покриває елемент 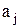 , якщо
, якщо та
та 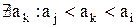
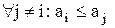 (
( 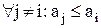 ). Найменший (найбільший) елемент називають мінорантою (мажорантою).
). Найменший (найбільший) елемент називають мінорантою (мажорантою).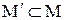 . Мінімальний (максимальний) елемент із множини мажорант (мінорант) називається верхньою (нижньою) гранню.
. Мінімальний (максимальний) елемент із множини мажорант (мінорант) називається верхньою (нижньою) гранню.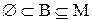 . Найменший (найбільший) елемент множини всіх верхніх (нижніх) граней
. Найменший (найбільший) елемент множини всіх верхніх (нижніх) граней 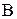 називається точною верхньою (нижньою) гранню множини
називається точною верхньою (нижньою) гранню множини  (
( 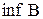 ).
).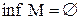 ; універсум
; універсум 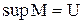 .
.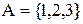 частково впорядкована відношенням включення
частково впорядкована відношенням включення 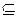 :
:  (рис. 5.5). Елемент
(рис. 5.5). Елемент 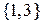 покриває елемент
покриває елемент  , тобто
, тобто 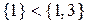 , отже,
, отже, 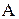 розглядаються дві підмножини:
розглядаються дві підмножини: 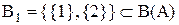 ;
; 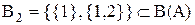 . Множина верхніх граней для
. Множина верхніх граней для 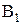 визначається як сукупність
визначається як сукупність 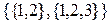 , нижня грань –
, нижня грань – 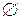 . Супремум
. Супремум 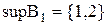 , інфімум
, інфімум 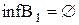 , при цьому жодна із зазначених граней не належить до B1. Mножина верхніх граней
, при цьому жодна із зазначених граней не належить до B1. Mножина верхніх граней  –
– 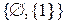 . Тоді
. Тоді 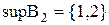 ,
, 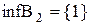 , тобто обидві точні грані належать множині
, тобто обидві точні грані належать множині 
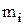 й
й 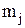 – два найбільших (найменших) елементи, тоді
– два найбільших (найменших) елементи, тоді 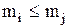 або
або 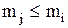 (
( 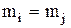 – єдиний найбільший (найменший) елемент. Що й було потрібно довести.
– єдиний найбільший (найменший) елемент. Що й було потрібно довести. (або
(або 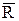 ) називається зворотнім до бінарного відношення
) називається зворотнім до бінарного відношення 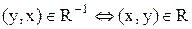 .
.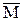 двоїсті, якщо
двоїсті, якщо 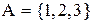 із приклада 5.5 задане зворотне відношення
із приклада 5.5 задане зворотне відношення  , яке можна проілюструвати діаграмою (рис. 5.6).
, яке можна проілюструвати діаграмою (рис. 5.6).
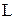 визначається як
визначається як 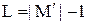 , де
, де 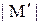 – потужність носія.
– потужність носія. .
.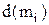 елемента
елемента 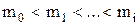 в
в 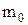 – мінімальний елемент множини
– мінімальний елемент множини 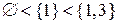 і
і 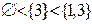 . Оскільки обидві ланцюги мають довжину 2, то висота елемента
. Оскільки обидві ланцюги мають довжину 2, то висота елемента 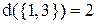 .
.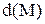 впорядкованої множини
впорядкованої множини 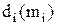 його елементів:
його елементів: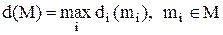 .
.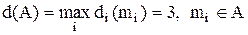 .
.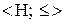 :
: 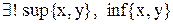 .
.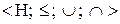 , для елементів якої справедливі закони ідемпотентності, комутативності, поглинання:
, для елементів якої справедливі закони ідемпотентності, комутативності, поглинання: ;
;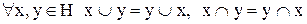 ;
; ,
,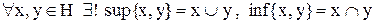 . (6.1)
. (6.1) . У якості
. У якості 
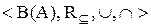 (рис. 6.2).
(рис. 6.2).
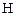 як структура
як структура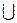 , перетинання
, перетинання 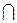 (додавання
(додавання 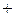 й множення
й множення  ; диз'юнкції
; диз'юнкції 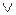 , кон’юнкції
, кон’юнкції 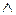 ), що задовольняють властивостям (властивості сформульовані в термінах теоретико-множинних операцій):
), що задовольняють властивостям (властивості сформульовані в термінах теоретико-множинних операцій): (ідемпотентність);
(ідемпотентність);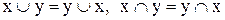 (комутативність);
(комутативність);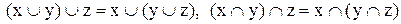 (асоціативність);
(асоціативність);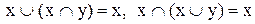 (елімінація)
(елімінація) . (6.2)
. (6.2) є підмножина структури
є підмножина структури 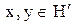 містить також їхнє об'єднання
містить також їхнє об'єднання 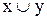 (sup) і перетинання
(sup) і перетинання 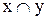 (inf) , тобто
(inf) , тобто