ДДНФ і ДКНФ функції можна одержати із ДНФ і КНФ шляхом еквівалентних перетворень.
Приклад 10.2. Одержати ДДНФ і ДКНФ функції із приклада 10.1.
Розв’язок. 1) Для одержання ДДНФ слід скористатися зображенням функції у вигляді ДНФ і застосувати закон протиріччя, помноживши кожний кон’юнктивний терм на 1 у вигляді добутку відсутньої змінної і її інверсії:

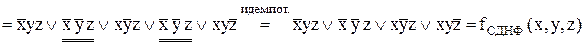 .
.
2) Для одержання ДКНФ слід скористатися зображенням функції у вигляді КНФ і застосувати закон виключеного третього з додаванням до кожного диз’юнктивного терму 0 у вигляді суми відсутньої змінної та її інверсії:

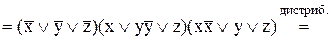
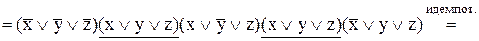
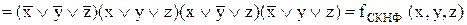
Зауваження. ДНФ, КНФ, ДДНФ, ДКНФ є різними форми зображення для однієї й тієї ж функції. Знаки рівності розуміються в змісті еквівалентності виконаних перетворень.
Досконалі ДНФ і КНФ можна одержати з таблиці істинності булевої функції. ДДНФ виписується за одиничним значенням функції, ДКНФ – за нульовими.
Приклад 10.3. Скласти таблицю істинності функції із приклада 10.1 і одержати досконалі ДНФ і КНФ за таблицею.
Розв’язок. Функція 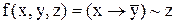 залежить від трьох змінних. Її таблиця істинності має вигляд:
залежить від трьох змінних. Її таблиця істинності має вигляд:
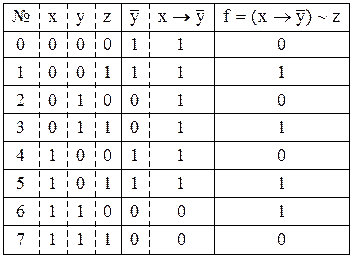
ДДНФ складається за одиничним значенням функції. При цьому кожному двійковому набору, на якому функція дорівнює одиниці, відповідає елементарна кон’юнкція, що складається з добутку первинних термів. Змінні, яким відповідають нульові значення, включаються під знак інверсії, а одиничні – без знака інверсії:
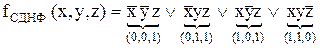 .
.
ДКНФ складається за нульовим значенням функції. При цьому кожному двійковому набору, на якому функція дорівнює нулю, відповідає елементарна диз’юнкція, що складається із суми первинних термів. Змінні, яким відповідають одиничні значення, включаються під знак інверсії, а нульові – без знака інверсії:
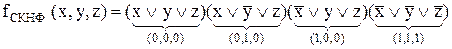 .
.
Якщо функція представлена таблицею істинності, можна відновити аналітичну форму функції у вигляді ДДНФ або ДКНФ.
10.3 Складність зображення булевих функцій
Визначення 10.8. Складність форми функції 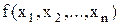 є число букв
є число букв 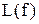 , що входять до
, що входять до 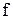 . Оцінка складності функції за Kвайном є
. Оцінка складності функції за Kвайном є 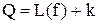 , де
, де 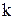 – число кон’юктивних термів функції.
– число кон’юктивних термів функції.
Зменшити функцію або її складність можна за допомогою законів булевої алгебри.
Приклад 10.4. Функція 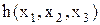 представлена таблицею істинності:
представлена таблицею істинності:
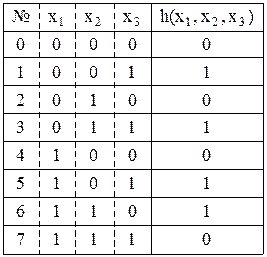
Формула, який вона задається, може мати вигляд ДДНФ або ДКНФ:
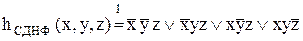 ,
,
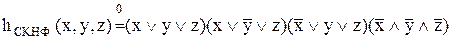 .
.
Складність функції 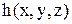 є
є 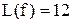 . Оцінка складності за Квайном є
. Оцінка складності за Квайном є  .
.
Отримані форми можна спростити до ДНФ і КНФ відповідно шляхом застосування дистрибутивного закону або закону склеювання для трьох змінних (якщо терми відрізняються тільки за однією змінною, вони підлягають склеюванню):

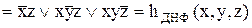 ,
,

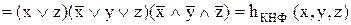 .
.
10.4 Теорема Шенона про розкладання булевих функцій
Теорема Шенона.Будь-яка булева функція 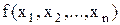 може бути зображеною у вигляді розкладання Шеннона за
може бути зображеною у вигляді розкладання Шеннона за 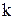 змінними:
змінними:
 (10.6)
(10.6)
де 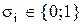 ,
, 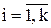 ,
, 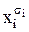 – первинні терми.
– первинні терми.
Слідство.Граничне розкладання Шенона при 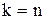 булевої функції
булевої функції 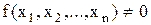 має вигляд
має вигляд
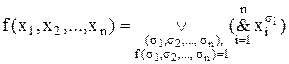 (10.7)
(10.7)
і є ДДНФ функції 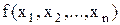 .
.
Теорема Шеннона є справедлива й у кон’юнктивній формі:
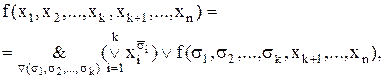 (10.8)
(10.8)
які в межі при 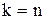 є ДКНФ функції:
є ДКНФ функції:
 . (10.9)
. (10.9)
10.5 Контрольні питання
1. Як визначається первинний терм?
2. Що являє собою елементарна кон’юнкція?
3. Що називається ДНФ функції?
4. Що таке елементарна диз’юнкція?
5. Що таке КНФ?
6. Як визначається ДДНФ?
7. Чим відрізняються ДНФ і КНФ?
8. Чим відрізняються ДНФ і СДНФ?
9. Як визначається ДКНФ?
10. Чим відрізняються КНФ і СКНФ?
11. Як складається ДДНФ за таблицею істинності?
12. Як можна одержати ДКНФ за таблицею істинності?
13. Як визначається складність формули?
14. Як визначається оцінка складності за Квайном?
15. Що являє собою розкладання Шеннона?
16. Що таке граничне розкладання Шеннона?
11 Елементи логічних схем. Булеві функції від двох змінних
Розглядаються основні властивості, фізичний зміст і схемотехнічне зображення булевих функцій від двох змінних для застосування їх при синтезі логічних схем.
11.1 Фізичний зміст логічних функцій І, АБО, НІ та їх схемотехнічне зображення
Розглядається простий бінарний елемент – вимикач, що має два стани. Якщо даний вимикач контролюється вхідною змінною 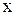 , то він виключений (розімкнутий) при
, то він виключений (розімкнутий) при 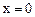 та включений (замкнений) при
та включений (замкнений) при 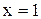 , як показано на рис.11.1:
, як показано на рис.11.1:
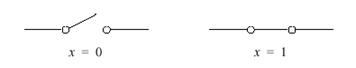
Рис. 11.1. Два стани вимикача
Можна використовувати наступне графічне позначення для зображення таких вимикачів (рис. 11.2):
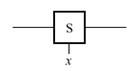
Рис. 11.2. Графічне зображення вимикача
Можливі варіанти з'єднання лампи із джерелом живлення, представлені наступними схемами (рис. 11.3):
Батарея 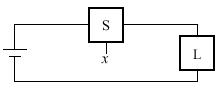 Лампа
Лампа
а
Джерело живлення 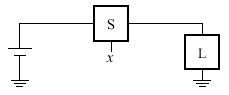 Лампа
Лампа
б
Рис. 11.3. Лампа, керована вимикачем: а – просте з'єднання з батареєю; б – використання заземлення
Використовуючи умовне позначення 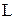 , можна описувати стан лампи як функції вхідної змінної
, можна описувати стан лампи як функції вхідної змінної 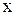 .
.
Якщо лампа горить, то 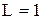 . Якщо лампа не світиться, то
. Якщо лампа не світиться, то 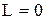 .
.
Оскільки 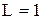 при
при 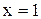 , і
, і 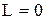 при
при 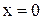 , то можна стверджувати, що
, то можна стверджувати, що 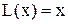 – логічна функція, де
– логічна функція, де 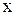 – логічна змінна. Це простий логічний вираз описує вихід як функцію від входу.
– логічна змінна. Це простий логічний вираз описує вихід як функцію від входу.
Розглянемо тепер можливість використання двох вимикачів для керування станом лампи, що схемотехнічно відповідає логічним функціям від двох змінних.
Нехай 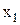 і
і  – керуючі змінні (входи) для цих вимикачів.
– керуючі змінні (входи) для цих вимикачів.
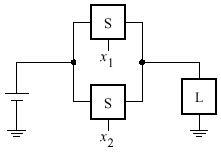
Вимикачі можуть бути з’єднані послідовно або паралельно, як показано на рис. 11.4.

а
б
Рис. 11.4. Дві основні функції: а – послідовне з’єднання (функція логічного множення AND); б – паралельне з’єднання (функція логічного додавання OR)
Послідовне з’єднання вимикачів. При послідовному з’єднанні лампа буде світитися тільки якщо обидва вимикачі включені (одночасно). Ця поведінка може бути описано логічним виразом:
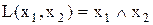 ,
,
де 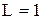 при
при 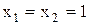 ,
, 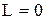 при
при 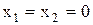 або
або 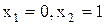 , або
, або 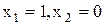 .
.
Символ кон’юнкції 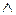 називається при цьому AND-оператором.
називається при цьому AND-оператором.
Говорять, що схема на рис. 11.4,а реалізує логічну AND-функцію (логічне множення).
Паралельне з’єднання вимикачів. При паралельному з'єднанні двох вимикачів лампа буде горіти, якщо вимикачі 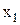 або
або  включені. Лампа також буде горіти, якщо обидва вимикачі включені одночасно. Лампа не буде горіти в єдиному випадку, якщо обидва вимикачі розімкнуті.
включені. Лампа також буде горіти, якщо обидва вимикачі включені одночасно. Лампа не буде горіти в єдиному випадку, якщо обидва вимикачі розімкнуті.
Ця ситуація може бути описана як функція логічного додавання 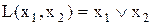 , де
, де 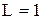 при
при 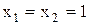 або
або 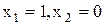 , а також
, а також 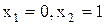 ;
; 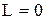 при
при 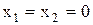 .
.
Символ диз’юнкції 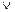 називається OR-оператором.
називається OR-оператором.
Схема на рис. 11.4,б реалізує логічну OR-функцію (логічне додавання).
У наведених вище виразах AND- і OR-оператори реалізують результат (вихід) 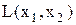 − логічну функцію із двома вхідними змінними.
− логічну функцію із двома вхідними змінними.
AND і OR є двома найбільш важливими логічними функціями. Разом з деякими іншими простими функціями вони можуть бути використані як складові частини (будівельні блоки) для реалізації логічних схем.
Наприклад, на рис. 11.5 показано, як три вимикачі можуть бути використані для керування лампою. Таке послідовно-паралельне з’єднання вимикачів реалізує логічну функцію 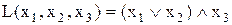 .
.
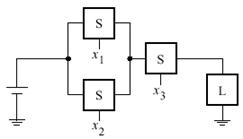
Рис. 11.5. Послідовно-паралельне з’єднання вимикачів
У цьому випадку лампа горить, якщо 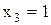 й одночасно
й одночасно 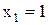 або
або 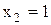 .
.
Інвертор. Для унарної операції інверсія, якій відповідає функція з однойменною назвою, схемотехничне зображення описується схемою, як показано на рис. 11.6:
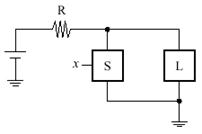
Рис. 11.6. Схема, що інвертує
У цьому випадку вимикач з’єднується в паралель із лампою. Лампа буде горіти, коли вимикач розімкнутий.
Формально така функціональна поведінка виражається як 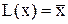 , де
, де 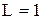 при
при 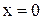 , і
, і 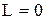 при
при 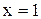 .
.
Значення цієї функції є зворотнім до значення вхідної змінної.
Поряд з використанням терміна інверсія можна застосовувати узагальнений термін доповнення (як у теорії множин). Таким чином, 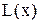 є доповнення
є доповнення 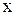 . У термінах операторів це є NOT-Оператор.
. У термінах операторів це є NOT-Оператор.
11.2 Таблиця аналітичного й схемотехнічного зображення булевих функцій від двох змінних
Фізичній схемі послідовного з’єднання (див. рис. 11.4,а) відповідає логічний примітив (блок) – двовхідний кон’юнктор, а схемі паралельного з’єднання (див. рис. 11.4, б) – диз’юнктор, схемі з інверсією (див. рис. 11.6) – інвертор. Елементи логічних схем і відповідні їм функції описані в таблиці 11.1.
Таблиця 11.1. Елементи логічних схем
| НАЗВА
| ПОЗНАЧЕННЯ
| СХЕМА
|
| Константа нуль
| 
| 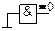
|
| Конъюнкция
| 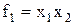
| 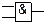
|
| Ліва зворотна імплікація
(коимпликация)
| 
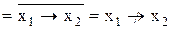
| 
|
Повторювач по 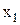
| 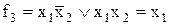
| 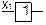
|
| Права зворотна
імплікація
| 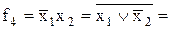
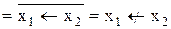
| 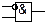
|
Повторювач по 
| 
| 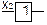
|
| Сума за mod 2 (нерівнозначність,
нееквівалентність)
| 
| 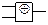
|
| Диз'юнкція
| 
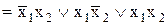
| 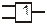
|
| Функція Вебба
| 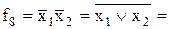
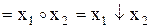
| 
|
| Функція рівнозначності
(еквівалентності)
| 
| 
|
Заперечення по 
| 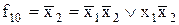
| 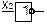
|
Права імплікація
(якщо  , те , те 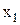 ) )
| 

| 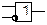
|
Заперечення по 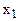
| 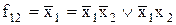
| 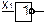
|
Ліва імплікація
(якщо 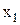 , те , те  ) )
| 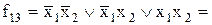
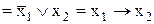
| 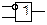
|
| Функція Шеффера
| 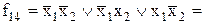

| 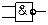
|
| Константа одиниця
| 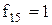
| 
|
Значення перерахованих булевих функцій від двох змінних наведені в таблиці 11.2.
Таблиця 11.2. Значення булевих функцій від двох змінних з таблиці 11.1
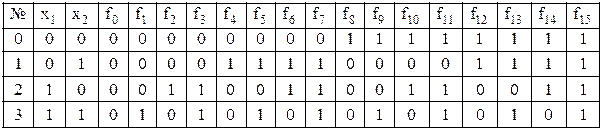
У світовій літературі мають місце наступні IEEE-Стандарти для позначень примітивів основних трьох булевых функцій (рис. 11.7).
а

б
в
Рис. 11.7. IEEE-Стандарти логічних блоків: двох- і n-входовий кон’юнктор (а); двох- і n-входовий диз’юнктор (б), інвертор (в)
11.3 Властивості й аналітичні подання елементарних булевих функцій від двох змінних
Функція додавання за mod 2: 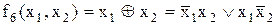 .
.
Справедливі комутативний і асоціативний закони:
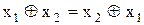 , (11.1)
, (11.1)
 . (11.2)
. (11.2)
Дистрибутивний закон має вигляд:
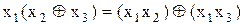 . (11.3)
. (11.3)
Мають місце аксіоми:
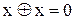 ,
,  ,
, 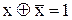 ,
, 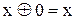 .
.
Зв'язок суми за модулем два з функціями кон’юнкції, диз'юнкції, інверсії встановлюється за формулами:
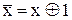 ; (11.4)
; (11.4)
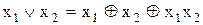 ; (11.5)
; (11.5)
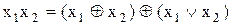 . (11.6)
. (11.6)
Функція імплікації:  .
.
Імплікація має властивість комутативності у вигляді:
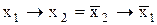 . (11.7)
. (11.7)
Асоціативний закон не виконується:
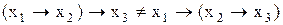 . (11.8)
. (11.8)
Аксіоми: 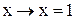 ;
; 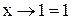 ;
; 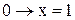 ;
;
 ;
; 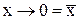 ;
; 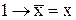 .
.
Установлюється зв'язок кон’юнкції, диз’юнкції, інверсії через імплікацію за наступними формулами:
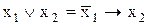 ; (11.9)
; (11.9)
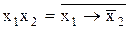 ; (11.10)
; (11.10)
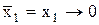 . (11.11)
. (11.11)
Функція Шефера має позначення | − штрих Шефера й обчислюється за формулою (інверсія кон’юнкції):  .
.
Властивість комутативності для двох змінних виконується:
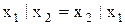 , (11.12)
, (11.12)
асоціативність не виконується:
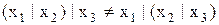 . (11.13)
. (11.13)
Аксіоми: 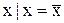 ;
; 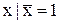 ;
;  ;
;  ;
; 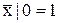 ;
; 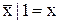 .
.
Формули перетворення:
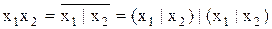 ; (11.14)
; (11.14)
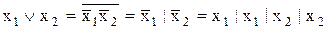 ; (11.15)
; (11.15)
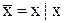 . (11.16)
. (11.16)
Функція Веба (Пірса) позначається за допомогою символу 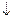 − стрілка Пірса й обчислюється за формулою (заперечення диз’юнкції):
− стрілка Пірса й обчислюється за формулою (заперечення диз’юнкції):
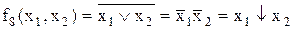 .
.
Властивість комутативності виконується:
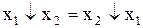 . (11.17)
. (11.17)
Аксіоми: 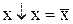 ;
; 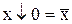 ;
; 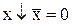 ;
; 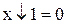 .
.
Формули перетворення функцій кон’юнкції, диз’юнкції, інверсії через функцію Веба:
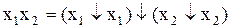 ; (11.18)
; (11.18)
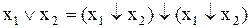 ; (11.19)
; (11.19)
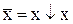 . (11.20)
. (11.20)
Таким чином, розглянуто аналітичне й схемотехничне зображення основних булевих функцій від двох змінних, які використовуються при синтезі й аналізі логічних схем
Функції AND і OR є найбільш важливими логічними функціями, які разом з функцією NOT максимально наближені до апаратурної реалізації цифрових систем Вони можуть бути використані як примітивні елементи для побудови й реалізації логічних схем.
11.4 Приклади розв’язання практичних завдань
Приклад 11.1.Синтезувати схему за логічним виразом
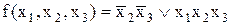 .
.
Розв’язок. Логічне вираз, яким задана функція, являє собою суму добутків – диз’юнкція елементарних кон’юнкцій (ДНФ). Кон’юнктивних термів два. Один з них складається з добутку інвертованих змінних  , що відповідає блоку 1 у схемі, де значення вхідних каналів 2 і 3 спочатку інвертуються, а потім перемножуються. Результатом є значення вихідного каналу 4, що, у свою чергу є вхідним для блоку 3 (рис. 11.8). Другий кон’юнктивний терм відповідає добутку всіх трьох змінних, від яких залежить функція:
, що відповідає блоку 1 у схемі, де значення вхідних каналів 2 і 3 спочатку інвертуються, а потім перемножуються. Результатом є значення вихідного каналу 4, що, у свою чергу є вхідним для блоку 3 (рис. 11.8). Другий кон’юнктивний терм відповідає добутку всіх трьох змінних, від яких залежить функція:  . Йому відповідає тривходовий кон’юнктор, де значення трьох вхідних каналів перемножуються (блок 2). Результатом є вихід 5, що є вхідним стосовно блоку 3. Блок 3, у свою чергу, є двовходовим диз’юнктором, де складаються значення з 5-й і 6-й ліній, а результатом є вихід 6, тобто задана функція.
. Йому відповідає тривходовий кон’юнктор, де значення трьох вхідних каналів перемножуються (блок 2). Результатом є вихід 5, що є вхідним стосовно блоку 3. Блок 3, у свою чергу, є двовходовим диз’юнктором, де складаються значення з 5-й і 6-й ліній, а результатом є вихід 6, тобто задана функція.
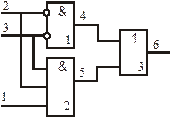
Рис. 11.8. Схемотехнічне зображення функції 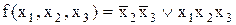
Приклад 11.2. Відновити аналітичну форму функції за схемою, зображеною на рис. 11.9:

Рис. 11.9. Схемотехнічне зображення функції від 5 змінних
Розв’язок. Для зручності опису схеми слід перенумерувати вхідні канали, внутрішні проміжні лінії, вихід, а також логічні блоки, при цьому номер блоку вказується в нижньому правому куті (рис. 11.10):
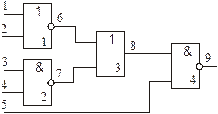
Рис. 11.10. Нумерація каналів і блоків на схемі з рис. 11.9
У блоці 1 виконується логічне додавання значень вхідних каналів 1 і 2, а потім результат інвертується, тобто вихід 6 відповідає виразу 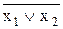 .
.
У блоці 2 перемножуються значення 3-го й 4-го каналів і результат інвертується: 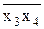 .
.



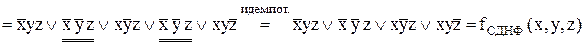 .
.
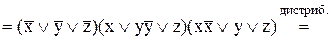
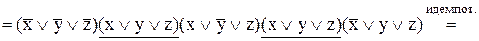
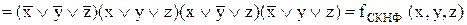
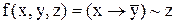 залежить від трьох змінних. Її таблиця істинності має вигляд:
залежить від трьох змінних. Її таблиця істинності має вигляд: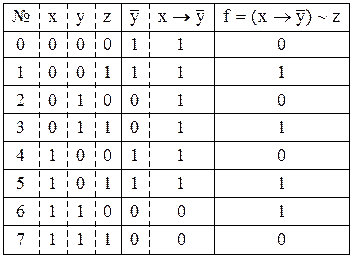
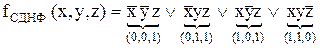 .
.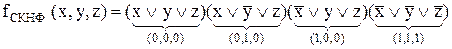 .
.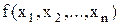 є число букв
є число букв 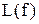 , що входять до
, що входять до 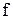 . Оцінка складності функції за Kвайном є
. Оцінка складності функції за Kвайном є 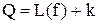 , де
, де 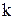 – число кон’юктивних термів функції.
– число кон’юктивних термів функції.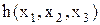 представлена таблицею істинності:
представлена таблицею істинності: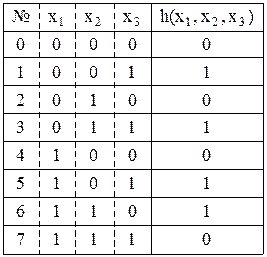
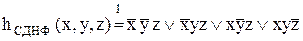 ,
,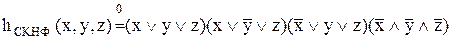 .
.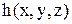 є
є 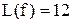 . Оцінка складності за Квайном є
. Оцінка складності за Квайном є  .
.
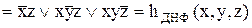 ,
,
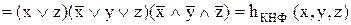 .
.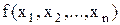 може бути зображеною у вигляді розкладання Шеннона за
може бути зображеною у вигляді розкладання Шеннона за  (10.6)
(10.6)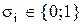 ,
, 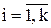 ,
, 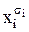 – первинні терми.
– первинні терми.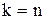 булевої функції
булевої функції 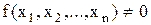 має вигляд
має вигляд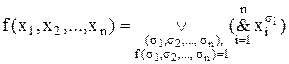 (10.7)
(10.7)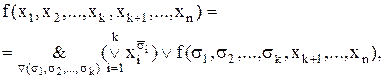 (10.8)
(10.8) . (10.9)
. (10.9)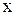 , то він виключений (розімкнутий) при
, то він виключений (розімкнутий) при 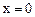 та включений (замкнений) при
та включений (замкнений) при 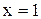 , як показано на рис.11.1:
, як показано на рис.11.1: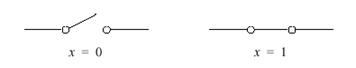

 Лампа
Лампа Лампа
Лампа , можна описувати стан лампи як функції вхідної змінної
, можна описувати стан лампи як функції вхідної змінної 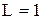 . Якщо лампа не світиться, то
. Якщо лампа не світиться, то 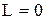 .
.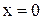 , то можна стверджувати, що
, то можна стверджувати, що 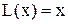 – логічна функція, де
– логічна функція, де 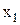 і
і  – керуючі змінні (входи) для цих вимикачів.
– керуючі змінні (входи) для цих вимикачів.

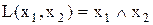 ,
,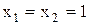 ,
, 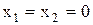 або
або 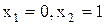 , або
, або 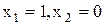 .
.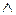 називається при цьому AND-оператором.
називається при цьому AND-оператором.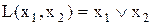 , де
, де 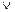 називається OR-оператором.
називається OR-оператором.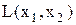 − логічну функцію із двома вхідними змінними.
− логічну функцію із двома вхідними змінними.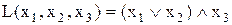 .
.
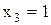 й одночасно
й одночасно 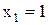 або
або 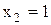 .
.
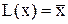 , де
, де 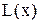 є доповнення
є доповнення 
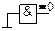
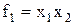
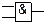

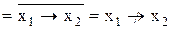

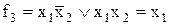
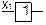
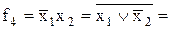
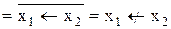
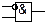

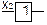

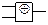

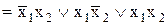
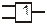



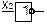


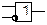
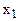
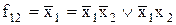
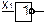
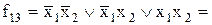
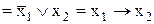
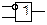
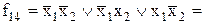

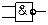
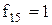
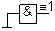
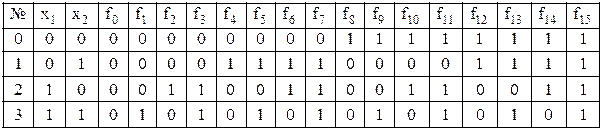
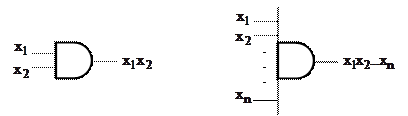


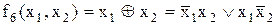 .
.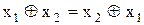 , (11.1)
, (11.1) . (11.2)
. (11.2)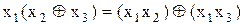 . (11.3)
. (11.3)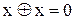 ,
,  ,
, 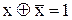 ,
, 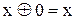 .
.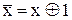 ; (11.4)
; (11.4)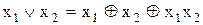 ; (11.5)
; (11.5)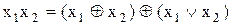 . (11.6)
. (11.6) .
.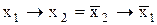 . (11.7)
. (11.7)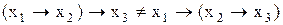 . (11.8)
. (11.8)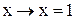 ;
; 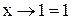 ;
; 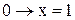 ;
; ;
; 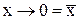 ;
; 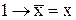 .
.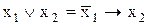 ; (11.9)
; (11.9)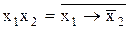 ; (11.10)
; (11.10)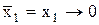 . (11.11)
. (11.11) .
.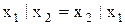 , (11.12)
, (11.12)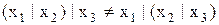 . (11.13)
. (11.13)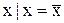 ;
; 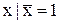 ;
;  ;
;  ;
; 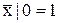 ;
; 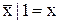 .
.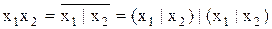 ; (11.14)
; (11.14)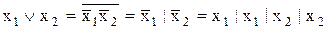 ; (11.15)
; (11.15)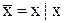 . (11.16)
. (11.16)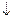 − стрілка Пірса й обчислюється за формулою (заперечення диз’юнкції):
− стрілка Пірса й обчислюється за формулою (заперечення диз’юнкції):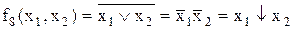 .
.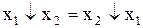 . (11.17)
. (11.17)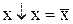 ;
; 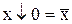 ;
; 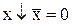 ;
; 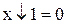 .
.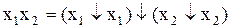 ; (11.18)
; (11.18)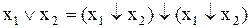 ; (11.19)
; (11.19)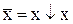 . (11.20)
. (11.20)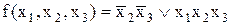 .
. , що відповідає блоку 1 у схемі, де значення вхідних каналів 2 і 3 спочатку інвертуються, а потім перемножуються. Результатом є значення вихідного каналу 4, що, у свою чергу є вхідним для блоку 3 (рис. 11.8). Другий кон’юнктивний терм відповідає добутку всіх трьох змінних, від яких залежить функція:
, що відповідає блоку 1 у схемі, де значення вхідних каналів 2 і 3 спочатку інвертуються, а потім перемножуються. Результатом є значення вихідного каналу 4, що, у свою чергу є вхідним для блоку 3 (рис. 11.8). Другий кон’юнктивний терм відповідає добутку всіх трьох змінних, від яких залежить функція:  . Йому відповідає тривходовий кон’юнктор, де значення трьох вхідних каналів перемножуються (блок 2). Результатом є вихід 5, що є вхідним стосовно блоку 3. Блок 3, у свою чергу, є двовходовим диз’юнктором, де складаються значення з 5-й і 6-й ліній, а результатом є вихід 6, тобто задана функція.
. Йому відповідає тривходовий кон’юнктор, де значення трьох вхідних каналів перемножуються (блок 2). Результатом є вихід 5, що є вхідним стосовно блоку 3. Блок 3, у свою чергу, є двовходовим диз’юнктором, де складаються значення з 5-й і 6-й ліній, а результатом є вихід 6, тобто задана функція.
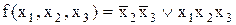


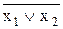 .
.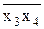 .
.