Чисту одиночну премію 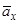 деколи плутають з поточним значенням
деколи плутають з поточним значенням 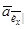 . Ці значення не співпадають; насправді справедлива нерівність
. Ці значення не співпадають; насправді справедлива нерівність
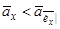 . (7.1)
. (7.1)
З врахуванням (6.7) и тотожності 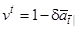 , де
, де 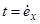 - число повних років до смерті людини в віці
- число повних років до смерті людини в віці 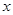 , справедлива рівносильна нерівність
, справедлива рівносильна нерівність
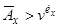 . (7.2)
. (7.2)
Кожна з цих нерівностей є прямим наслідком нерівності Йєнсена; наприклад, друга нерівність означає
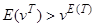 , (7.3)
, (7.3)
що очевидно, оскільки 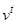 є випуклою функцією від
є випуклою функцією від 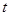 .
.
Метою розділу є узагальнення цих нерівностей. Будемо розглядати чисту одиночну премію 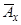 , як функцію сили відсотка
, як функцію сили відсотка 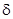 :
:
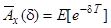 ; (7.4)
; (7.4)
це є перетворення Лапласа розподілу змінної 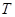 . Визначимо також функцію
. Визначимо також функцію
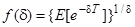 ,
, 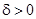 . (7.5)
. (7.5)
Для малих значень 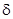 можна апроксимувати (7.4) величиною
можна апроксимувати (7.4) величиною 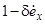 . Тому
. Тому 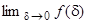 існує і має значення
існує і має значення
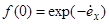 . (7.6)
. (7.6)
Лема. Функція 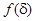 монотонно зростає
монотонно зростає
Для доведення візьмемо два додатних числа 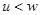 і покажемо, що
і покажемо, що
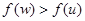 . (7.7)
. (7.7)
З нерівності Йєнсена випливає
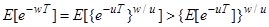 . (7.8)
. (7.8)
Тому
 , (7.9)
, (7.9)
звідки маємо (7.7), що й доводить лему.
З леми випливає, що 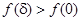 , тому
, тому
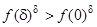 . (7.10)
. (7.10)
З (7.6) можна також знову отримати нерівність (7.2).
Розглянемо три різні сили відсотка 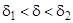 . З леми маємо
. З леми маємо
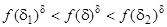 , (7.11)
, (7.11)
тому
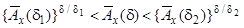 , (7.12)
, (7.12)
що дозволяє оцінити 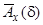 за значеннями
за значеннями 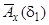 і
і 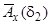 .
.
Наприклад, нехай
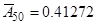 для
для 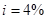 ,
,
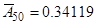 для
для 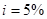 .
.
Тепер можна знайти границі для чистих одиночних премій 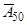 і
і 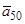 при
при 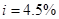 . З (7.12) при
. З (7.12) при
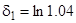 ,
, 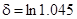 ,
, 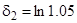
відразу маємо
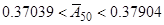 .
.
З тотожності 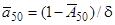 отримуємо
отримуємо
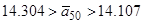 .
.
Замінивши 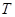 на
на 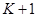 і
і 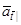 на
на
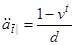 ,
, 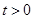 , (7.13)
, (7.13)
отримуємо нерівності
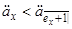 , (7.14)
, (7.14)
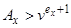 , (7.15)
, (7.15)
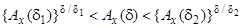 (7.16)
(7.16)
за допомогою аналогічних міркувань.
Перші дві похідні функції 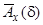 дорівнюють
дорівнюють
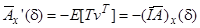 ,
,
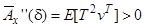 . (7.17)
. (7.17)
Таким чином 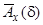 - монотонно спадна і опукла функція від
- монотонно спадна і опукла функція від 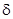 . Тому довільна частина кривої лежить нижче січної
. Тому довільна частина кривої лежить нижче січної
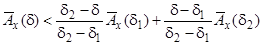 , (7.18)
, (7.18)
але вище дотичних
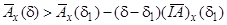 ,
,
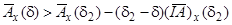 . (7.19)
. (7.19)
Деколи оцінки (7.18), (7.19) виявляються кращими від оцінки (7.12). Для наведеного прикладу верхня оцінка, яка отримана з (7.18), має вид
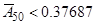 .
.
Нижня границя для 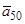 також покращена
також покращена
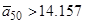 .
.


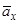 деколи плутають з поточним значенням
деколи плутають з поточним значенням 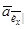 . Ці значення не співпадають; насправді справедлива нерівність
. Ці значення не співпадають; насправді справедлива нерівність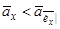 . (7.1)
. (7.1)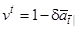 , де
, де 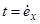 - число повних років до смерті людини в віці
- число повних років до смерті людини в віці 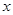 , справедлива рівносильна нерівність
, справедлива рівносильна нерівність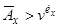 . (7.2)
. (7.2)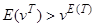 , (7.3)
, (7.3)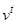 є випуклою функцією від
є випуклою функцією від 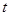 .
.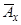 , як функцію сили відсотка
, як функцію сили відсотка 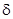 :
: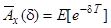 ; (7.4)
; (7.4)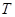 . Визначимо також функцію
. Визначимо також функцію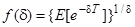 ,
, 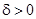 . (7.5)
. (7.5)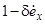 . Тому
. Тому 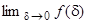 існує і має значення
існує і має значення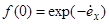 . (7.6)
. (7.6)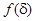 монотонно зростає
монотонно зростає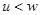 і покажемо, що
і покажемо, що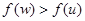 . (7.7)
. (7.7)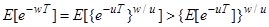 . (7.8)
. (7.8) , (7.9)
, (7.9)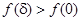 , тому
, тому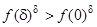 . (7.10)
. (7.10)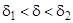 . З леми маємо
. З леми маємо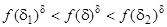 , (7.11)
, (7.11)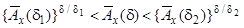 , (7.12)
, (7.12)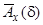 за значеннями
за значеннями 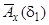 і
і 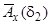 .
.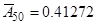 для
для 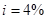 ,
,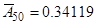 для
для 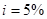 .
.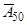 і
і 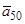 при
при 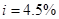 . З (7.12) при
. З (7.12) при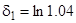 ,
, 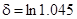 ,
, 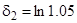
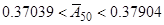 .
.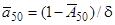 отримуємо
отримуємо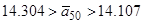 .
.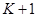 і
і 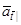 на
на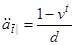 ,
, 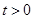 , (7.13)
, (7.13)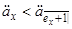 , (7.14)
, (7.14)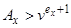 , (7.15)
, (7.15)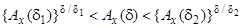 (7.16)
(7.16)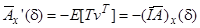 ,
,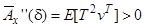 . (7.17)
. (7.17)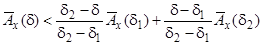 , (7.18)
, (7.18)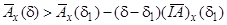 ,
,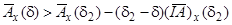 . (7.19)
. (7.19)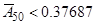 .
.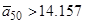 .
.