Під математичним предметним моделюванням розуміють спосіб дослідження фізичних процесів шляхом вивчення явищ, що мають відмінне від досліджуваних фізичний зміст, але описуваних однаковими з ними співвідношеннями. У простих випадках для цієї мети використовують відомі аналогії між механічними, електричними і іншими явищами. Класичним прикладом тут служить аналогія між розподілом електричного потенціалу U і сталим розподілом температури Т усередині однорідного ізотропного тіла.
Рівняння теплопровідності Фур'є, виражене у відносних координатах:
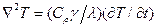 (4.30)
(4.30)
і рівняння, відповідне електричним явищам в сітці з r і С:
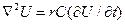 (4.31)
(4.31)
мають ідентичну структуру.
Якщо за номінальні одиниці набудемо яких-небудь значень То, Uо, tо, rо, Со, γо, λо, то в відносній системі одиниць отримаємо Т' = Т/Т0; U' = U/U0; t'=t/ t0; С'р ==СР/Сро; γ' = γ/γо; λ' = λ/λо; r' = r/r0; С' = С/С0; х'= х/х0, у' = y/yо; z' = z/zо. Тоді дані рівняння у відносній системі одиниць наберуть вигляду
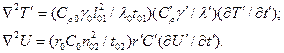 (4.32)
(4.32)
(4.33)
У електричній моделі число елементів п відповідає довжині l в просторових координатах. Тому як номінальна величина п0 можна вибрати деяке число n02.
Комплекси номінальних значень, ув'язнені в дужках, згідно теорії Фур'є про розмірність фізичних рівнянь, є безрозмірними фізичними величинами. Для груп подібних явищ одного і того ж класу, відповідних одному і тому ж вигляду диференціального рівняння, безрозмірні комплекси, взяті в дужках мають бути тотожні:
Cp0γ0l012/λ0t01 = r0C0n022/t02 (4.34)
Позначимо відношення величин, утворюючих умови однозначності в зразку і моделі, константами подібності: l0/n02 = n1; t01/t02 = nt; (Cp0γ0/ λ0)/r0C0 = na. Вибір множників подібності обмежимо, наклавши умову nanl/nt = l.
Аби побудувати штучну електричну модель, потрібно провести подібне перетворення умов однозначності системи зразка, інваріантне відносно її критеріїв. Тоді можна одні і ті ж елементи електричних моделей використовувати для вирішення різних практичних завдань.
У математичному моделюванні широко використовують аналогові (АВМ) і цифрові (ЦВМ) обчислювальні машини. АВМ видають рішення у вигляді осцилограм на екрані електронно-променевої трубки. Такі машини застосовують, якщо потрібна не стільки висока точність, скільки наочність процесу. Істотний недолік АВМ загального призначення - відсутність автоматичного введення інформації. Програму (схему моделі) і вихідні дані вводять в машину уручну за допомогою шнурової комутації і потенціометрів, що обертаються. Це вимагає багато часу і великої напруги експериментатора, проте часто окупається тим, що, на відміну від ЦВМ, час рішення на АВМ мало залежить від складності завдання і складає, як правило, секунди.
Сучасні ЕОМ складаються з великої кількості обчислювальних елементів, операційних блоків і вузлів різного призначення. Моделювання в них різного роду ланок - масштабних, інтегруючих, диференціюючих, таких, що підсумовують, інерційних, форсуючих - здійснюється за допомогою вирішуючих підсилювачів, включених у відповідні схеми.
Розглянемо приклад моделювання на АВМ волочіння металу через систему з декількох волок, що коливаються.
Відомо, що волочіння металу через волоки, що коливаються, за певних умов дає можливість збільшити обтиски. У одних випадках це досягається за рахунок зменшення сил тертя і зниження опору деформації. У інших - за рахунок того, що дріт обробляється декількома послідовно розташованими волоками, коливання яких погоджені таким чином, що кожна з них навантажується по черзі. Якщо технологічний процес ведуть відповідно до останнього способу, величина результуючого обтиску і швидкість волочіння залежать від числа послідовно розташованих волок, розподілу обтисків між ними, швидкості коливальних рухів кожної з них і деяких інших чинників. Відшукати раціональні параметри установки і режими ведення процесу в цьому випадку - серйозне завдання. Проте із-за складності і нелінійності систем диференціальних рівнянь, що описують процес в динаміці, аналітичне рішення цієї задачі вельми ускладнено. У зв'язку з цим було здійснено математичне моделювання такого процесу на АВМ.
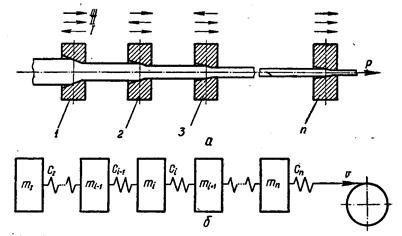
Рис.4.3 Схема волочіння металу через декілька рухливих волок (а) і його розрахункова схему (б); стрілки над волоками показують напрями руху волок в певні моменти часу
Аби застосувати АВМ, потрібно спочатку розробити модель, яка з достатньою мірою наближення відобразить основні характеристики процесу, що вивчається.
При розробці такої моделі розглядався загальний випадок волочіння через п послідовно розташованих рухливих волок (рис.4.3, а). Після заправки дріт деформується волокою 1, яка в даний момент рухається назустріч металу (напрями стрілок I). Останні волоки (2, 3, ..., п) в цей час здійснюють холостий хід, рухаючись разом із дротом. Волочіння в них не відбувається. Після закінчення робочого ходу волоки 1 (назустріч металу) починається робочий хід волоки 2 (напрями стрілок II); всі останні волоки рухаються разом із дротом. Потім здійснює робочий хід волока 3 (напрями стрілок III) і так далі.
Розрахункова схема, прийнята при моделюванні, представлена на рис.4.3, б. Волоки і пов'язані з ними рухомі частини приводу змальовані тут у вигляді зосереджених мас mi (i - порядковий номер волоки), що здійснюють зворотно-поступальні рухи уздовж осі волочіння з швидкістю vi. Відрізки оброблюваного металу поміж волоками розглядаються як пружні елементи. Оскільки розмах коливань волок істотно менше відстані між ними, коефіцієнт жорсткості металу на кожній ділянці Сi вважається величиною постійною. Приведена розрахункова схема полегшує аналіз режимів роботи установки і складання рівнянь, що виражають кількісний взаємозв'язок між основними параметрами досліджуваного процесу.
Аналізуючи умови, в яких знаходяться відрізки дроту поміж волоками, можна встановити, що із-за різниці в швидкостях руху переднього і заднього кінців кожного відрізку вони піддаються пружній деформації. Відповідно до закону Гука силу, що виникає при цьому в металі, можна виразити через цю деформацію:
 (4.35)
(4.35)
Тут Pyi - сили пружної деформації дроту на ділянці між i-йі (i+1)-й волоками; Ру0 - початкове значення сили пружної деформації дроту у момент часу t = 0 на тій же ділянці; Ci = Esi/li - коефіцієнт жорсткості смуги; Е - модуль подовжньої пружності матеріалу дроту; si - площа поперечного перетину дроту на відповідній ділянці; li - середня відстань поміж i-оїі (i+1) волоками; vi, vi+1 - швидкості руху відповідних волок; vi', v'i+1- відносні швидкості руху дроту біля входу у відповідні волоки; μi- коефіцієнт витяжки в i-йволоці; t - час.
Безпосередньо на волоку і пов'язані з нею рухомі деталі установки діють дві сили: сила Qi, що розвивається приводом, і сила осьового тиску металу на волоку. Перша з них є функцією декілька змінних:
Qi = fi(Zi, xi, vi, t), (4.36)
де Zi - сигнал управління приводом i-оїволоки; xi- координата, що позначає зсув i-ї волоки відносно початкового положення уздовж осі волочіння. Конкретно взаємозв'язок між змінними, що входять в цей вираз, визначається типом приводу волок (електромагнітний, електродинамічний, гідравлічний) і його конструктивними особливостями.
Силу осьового тиску металу на волоку можна визначити таким чином:
Po.д.i = Pyi – Py(i-1) (4.37)
Цей вираз справедливий як для моменту холостого ходу волоки, коли vi' = 0 і волочіння в ній не відбувається, так і для робочого ходу, коли vi' > 0.
З іншого боку, відомо, що як сила волочіння, так і сила осьового тиску металу на волоку знаходяться в лінійній залежності від величини противонатяжения. Тому в режимі волочіння для i-йволоки повинна виконуватися умова
Po.д.i = Poi – (1 – bi)P y(i-1) (4.38)
де Poi - сила осьового тиску металу на волоку при волочінні без противонатягу; bi - коефіцієнт, що враховує вплив противонатягу на силу волочіння. У даному випадку в ролі противонатягу виступає сила пружної деформації відрізку дроту, що знаходиться між i (i+1)-й волоками.
Відносна швидкість металу біля входу в i-уволоку визначається по-різному залежно від того, має місце процес волочіння в i-йволоке чи ні:
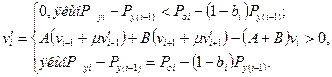 (4.39)
(4.39)
Тут
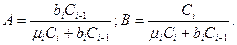 (4.40)
(4.40)
Перша умова відповідає відсутності, а друге - наявності процесу волочіння в даній волоці.
Для визначення швидкості волоки можна скористатися рівнянням руху:
midvi/dt = Po.д.i+Qi (4.41)
Відхилення волоки від початкового положення xoi визначається наступним виразом:
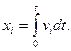 (4.42)
(4.42)
Сигнали управління приводом волок, формовані блоком управління (БУ), можуть бути функцією декілька змінних:
Zi = φi(x1, x2, ... , хп, vi, t), (4.43)
вигляд якої залежить від алгоритму роботи БУ і його схемного і конструктивного рішення.
Отримана система рівнянь (4.34) - (4.42) досить повно описує процес волочіння металу через декілька волок, що по черзі навантажуються. У разі потреби ці рівняння можна доповнити обмеженнями, що відображають конструктивні особливості конкретної установки. Зазвичай ці обмеження накладають на відхилення волоки від початкового положення, її швидкість, на силу, що розвивається приводом волоки і так далі Реалізація цих обмежень при моделюванні процесу зазвичай не зустрічає утруднень.
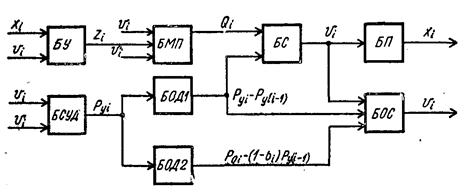
Рис.4.4 Блок-схема моделі установки з n рухливими волоками.
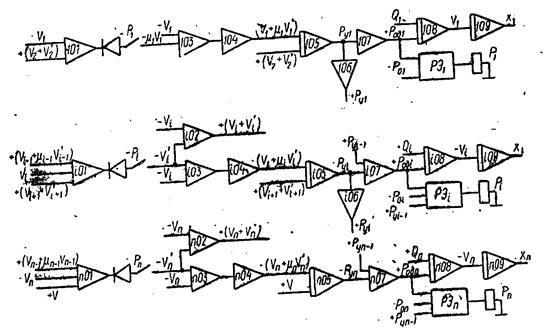
Рис.4.5 Структурна схема моделі.
Умовно блок-схему вирішення отриманої системи рівнянь (рис.4.4) можна розділити на дві частини. У першу увійдуть блок управління БУ, що реалізовує вирішення рівняння (4.43), і блок моделювання приводу БМП, призначений для вирішення рівнянь (4.36), що відображають роботу приводу волок. Другу частину схеми складуть останні блоки, за допомогою яких відпрацьовуються величини, що характеризують технологічні параметри процесу. Функціональне призначення цих блоків наступне: БСУД - блок обчислення пружної деформації відрізків дроту, розташованих між суміжними волоками; БОД1 і БОД2 - блоки визначення сили осьового тиску металу на волоку відповідно по рівняннях (4.37) і (4.38); БОС – блок, що виробляє величину відносної швидкості руху металу біля входу у волоку; БС - блок обчислення швидкості руху волок; БП - блок обчислення положення волок.
Прийняте ділення блок-схеми на дві частини обумовлене тим, що моделювання процесу може мати дві різних мети: 1) вибір типа приводу волок, схеми управління і їх раціональних параметрів; 2) дослідження впливу технологічних параметрів (режим обтисків, швидкість волочіння, кількість волок і т. д.) на процес і вибір їх оптимального поєднання.
Оскільки питання моделювання приводів і схем управління вистачає і які добре висвітлені в спеціальній літературі, тут ми на них зупинятися не будемо, а розглянемо структурну схему моделі, що відображає взаємозв'язок технологічних параметрів.
Запропонована схема (рис.4.5) розроблялася так, щоб моделювання параметрів, що відображають зміну в процесі роботи стану волоки і пов'язаної з нею штаби металу, здійснювалося за допомогою типового вічка. Таке рішення дає можливість легко змінювати при моделюванні кількість волок, що беруть участь в процесі.
Підсилювач i 01, діод, реле Рi, і релейний елемент РЕ вирішують вираз (4.39), визначаючи тим самим відносну швидкість металу біля входу у волоку. За допомогою підсилювачів i 02, i 03 знаходиться абсолютна швидкість металу біля входу і на виході з волоки. Інтегратор i 05 вирішує рівняння (4.35) відносно Pyi, суматор i 07 відповідно до (4.37) відпрацьовує Po.д.i. За допомогою інтеграторів i 08 і i 09 по рівняннях (4.41) і (4.42) визначаються швидкості волоки vi і зсуви xi уздовж осі волочіння від вихідної точки. Підсилювачі i 04 і i 06 служать для зміни знаку.
Розроблена схема дає можливість отримати осцилограми швидкості, положення волок, сил пружної деформації смуги на різних ділянках і сил осьового тиску металу на волоки. Крім того, вона дозволяє легко і швидко змінювати режими роботи і параметри модельованої системи і спостерігати вплив цих змін на характер роботи установки, що вивчається.
Розробляючи алгоритм управління приводами волок, потрібно передбачати паузи між моментами відключення одного приводу і включення наступного, що дозволяють унеможливити одночаснє волочіння металу в двох волоках.
Досить простим і ефективним виявився метод програмного управління приводом у поєднанні з управлінням у функції шляхои за допомогою МПРУ.


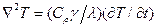 (4.30)
(4.30)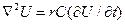 (4.31)
(4.31)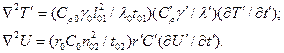 (4.32)
(4.32)
 (4.35)
(4.35)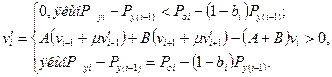 (4.39)
(4.39)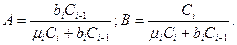 (4.40)
(4.40)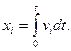 (4.42)
(4.42)
