ВИБІР ВИМІРЮВАЛЬНОЇ АПАРАТУРИ ТА ОЦІНКА ПОХИБОК ВИМІРУ
Вибір типа апаратури, вимірювальної схеми і її елементів визначається цілями і умовами проведення експерименту, тобто характером вимірюваних параметрів (статичні або динамічні), необхідною точністю вимірів, часом протікання процесу, швидкістю зміни параметрів, числом одночасно реєстрованих величин, межами їх зміни і ін.
При вимірі і реєстрації статичних величин визначальним чинником є точність засобів вимірів. Для дослідження динамічних процесів первинне значення набуває швидкодія вимірювальної апаратури, тобто діапазон її робочих частот, який повинен перекривати максимальну частоту процесу. Для вимірювальної установки, що включає декілька елементів (датчик, підсилювач, реєструючий прилад), робочий діапазон визначається елементом, що має мінімальний діапазон (межа) робочих частот. Так, для найгрубіших шлейфових гальванометрів верхня межа робочих частот не перевищує 5000-6000 Гц, а для найвідчутливіших - 10...60 Гц.
Робочий діапазон частот в установках, зібраних за безпідсилювальними схемами, обмежений найчастіше частотною характеристикою шлейфів, а в підсилювальних схемах - несучою частотою (при роботі на змінному струмі). В деяких випадках лімітуючою виступає власна частота коливань чутливих елементів датчиків.
Таким чином, для правильного вибору засобів вимірів - датчиків, підсилювачів, реєструючих приладів - потрібно знати частотний діапазон, спектр частот або хоч би максимальну частоту досліджуваного процесу.
Вибираючи апаратуру, потрібно погоджувати опори входу і виходу елементів вимірювальної установки. Це особливо важливо при виборі гальванометрів для шлейфових осцилографів, для яких узгодження вихідного опору вимірювального тракту з опором гальванометра важливе і з точки зору демпфування.
З випадкових (невраховуємих) чинників на точність виміру впливають ті, які приводять до нестабільності параметрів вимірювальної системи:
1) неоднорідність деформованого стану пружних елементів датчиків при навантаженні (ця неоднорідність обумовлена конструкцією і співвідношенням розмірів пружного елементу, а також додатковою напругою від перекосу, вигину, скручування і т. п.);
2) коливання напруги живлення вимірювального ланцюга;
3) нестабільність характеристик підсилювача (зміна чутливості, дрейф нуля і т. д.);
4) наведення від зовнішніх електромагнітних полів, вплив паразитних ємкостей і пр.;
5) випадкові струси, вібрація реєструючих приладів (цей чинник особливо впливаючий для осцилографів з чутливими шлейфами).
Врахувати заздалегідь вплив випадкових чинників при вимірах практично не можливо. Проте, маючи в своєму розпорядженні відповідні дослідні дані і користуючись методами математичної статистики, міру впливу цих чинників на точність виміру можна прогнозувати.
При виборі засобу вимірів слід завжди мати на увазі, що точність вимірювального приладу і точність результату вимірів - не одне і теж саме. Точність результату можна підвищити за рахунок збільшення числа повторних вимірів одного і того ж параметра. Враховуючи, що підвищення точності засобу вимірів, як правило, пов'язане із збільшенням його вартості, слід в розумних межах розміряти точність засобу вимірів з кількістю випробувань. Потрібно прагнути використовувати по можливості недороге устаткування, прилади потрібної, а не завищеної точності, робити стільки відліків, скільки потрібно для досягнення заданої точності вимірюваної величини. Невиправдане використання приладів високої точності, планування завищеної кількості випробувань ведуть до зайвих матеріальних витрат і знижують ефективність досліджень.
5.2. Визначення максимальної частоти процесу
Зміна в часі таких параметрів, як сила, тиск, швидкість деформації і ін., є складним динамічним або стато-динамічним процесом, що характеризується періодичним графіком. Всякий складний періодичний процес можна представити сумою синусоїдальних складових, розклавши його в ряд Фур'є. В разі одиничного або аперіодичного процесу розкладання на складові проводять за допомогою інтеграла Фур'є.
Розкладання процесу на постійну і ряд гармонійних складових дає можливість представити реєстрацію складного процесу вимірювальним приладом у вигляді реакції приладу на кожну із складових. При гармонійному аналізі функцію x=x(t), що описує періодичний графік, представляють у вигляді тригонометричного ряду Фур'є, що складається з постійної а0/2 і нескінченної суми гармонік:
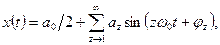 (5.1)
(5.1)
де ω0 = 2π/T0; T0 = 1/n0 - період процесу; z - порядковий номер гармоніки. Амплітуда аz і фаза ωz гармонік визначаються формулами
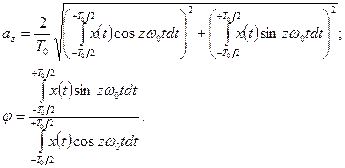 (5.2)
(5.2)
(5.3)
Постійна складова а0/2, яка є середнім значенням функції x(t) за період Т0,
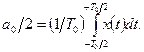 (5.4)
(5.4)
В теорії рядів Фур'є доводиться, що із збільшенням z амплітуди гармонік зменшуюються до нуля. Отже, процес x(t) з деяким наближенням можна описати кінцевою сумою гармонік. Вважається, що процес досить точно описується такою сумою, в якій остання гармоніка, що враховується, має амплітуду, приблизно в 10 разів меншу амплітуди першої, основної гармоніки з частотою ω0. Частоту останньої гармоніки, що враховується, називають максимальною частотою процесу. Таким чином, для визначення максимальної частоти періодичного процесу досить досліджувати залежність амплітуд гармонік від частоти.
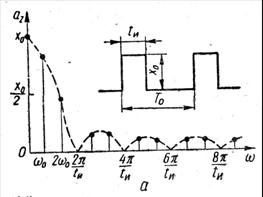
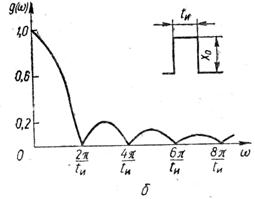
Рис.5.1 Спектри графіків: а - періодичної функції; б - одиничного імпульсу.
Для прямокутного імпульсу, до якого близькі параметри графіків прокатки і деяких інших процесів ОМТ, залежність аz від частоти zω0 має вигляд:
 (5.5)
(5.5)
де х0, tи, T0 - відповідно амплітуда, тривалість і період імпульсу.
На рис.5.1, а приведений графік залежності аz від частоти ω = zω0 при tи/T0 = 1/3. На частотах, що задовольняють умові ωtи/2 — kπ (k=1, 2, 3, …), аz набуває нульових значень. Це означає, що гармонік з номерами z = 3k немає. Амплітуди гармонік:
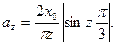 (5.6)
(5.6)
Зокрема,
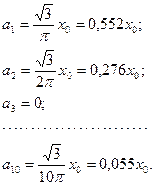 (5.7 - 5.10)
(5.7 - 5.10)
Таким чином, максимальна частота процесу дорівнює частоті 10-ої гармоніки.
Якщо графік вимірюваної величини неперіодичний, то ряд Фур'є згортається в інтеграл Фур'є:
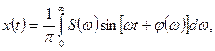 (5.11)
(5.11)
де
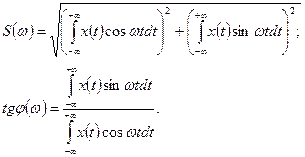 (5.12 - 5.13)
(5.12 - 5.13)
Тут S (ω) має сенс «щільності», з якою на осі частот розподілені амплітуди гармонік, складові процесу х(t). Тому S(ω) називається спектральною щільністю процесу. Для прямокутного імпульсу:
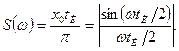 (5.14)
(5.14)
На рис.5.1, б приведена залежність
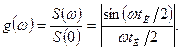 (5.15)
(5.15)
Функція g(ω) називається нормованою спектральною щільністю. В даному випадку максимальна частота процесу - частота, при якій g(ω) = 0,l. З рис.5.1, б видно, що при ω>6π/tи функція g(ω)<0,1. Отже, максимальну частоту процесу вигляду одиночного прямокутного імпульсу тривалістю tи можна прийняти рівною ωmax = 6π/tи, або
nmax = ωmax/2π = 3/tи (5.16)
Для процесів з формою імпульсу, що відрізняється від прямокутної, наприклад трапецеїдальною, nmax = 3/tи. Тому незалежно від форми графіка максимальну частоту процесу з деяким запасом можна визначати по формулі (5.16).


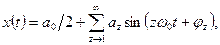 (5.1)
(5.1)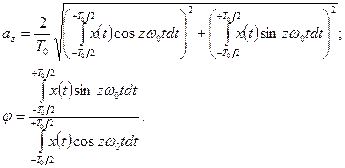 (5.2)
(5.2)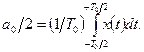 (5.4)
(5.4)

 (5.5)
(5.5)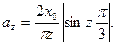 (5.6)
(5.6)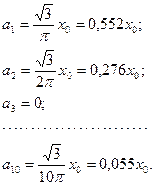 (5.7 - 5.10)
(5.7 - 5.10)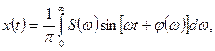 (5.11)
(5.11)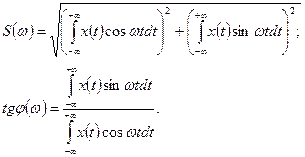 (5.12 - 5.13)
(5.12 - 5.13)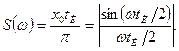 (5.14)
(5.14)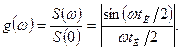 (5.15)
(5.15)