Для того, щоб користуватися закономірностями законів подібності, потрібно при фізичному моделюванні створювати такі умови, при яких забезпечується, з одного боку, геометрична подібність моделі і натури, а з іншої - фізична подібність процесів, що протікають в них при подібній деформації. Теоретично цього можна досягти, виконуючи критерії подібності. У реальних же умовах моделювання це не досягається, причому в інших випадках відступи від вимог теорії вельми істотні.
При моделюванні з практично достатньою точністю забезпечуються приблизні:
1) геометрична подібність моделі і натури;
2) геометрична подібність інструменту моделі і натури;
3) подібність обтисків моделі і натури;
4) подібність складу металу моделі і натури: метали можуть відноситися до однієї марки, але до різних плавок; замість литого часто використовують вже деформований метал.
Крім того, відбувається наступне:
1) умови нагріву моделі (атмосфера печі, тривалість нагріву) відрізняються від умов нагріву натури; температури деформації заміряються лише приблизно;
2) швидкості охолодження моделі і натури неоднакові, у зв'язку з чим температура деформації моделі не збігається з температурою деформації натури;
3) швидкість деформації точно не задовольняє жодному з критеріїв кінематичної подібності.
Не дивлячись на відмічені невідповідності, наближене моделювання правомірне, оскільки його результати у багатьох випадках сповна задовольняють практику.
Загальноприйнятої методики наближеного моделювання поки що немає. По одному з методів пропонується, не добиваючись повної теплової подібності моделі і натури, тобто однакових температур в подібних точках, проводити гарячу деформацію при рівності середніх за об'ємом температур моделі і натури і дотриманні швидкісної умови εM = εH; vM = vH/m. Проте цей метод вимагає деформації моделі в печі (для підтримки її температури на відповідному рівні), що практично здійснити важко.
Неминучі при моделюванні відступи від принципу подібності слід компенсувати розрахунковам шдяхом, застосовуючи експериментально встановлені коефіцієнти. Вплив розбіжності в швидкості деформації можна враховувати швидкісним коефіцієнтом φс, що показує, в скільки разів збільшиться напруга текучості при тому або іншому збільшенні швидкості деформації ε (табл.4.2).
Таблиця 4.2 Значення швидкісного коефіцієнта φс
| Відношення швидкостей деформації
| Температури деформації
|
| Т/ Тпл<0,3
| Т/ Тпл=0,3-0,5
| Т/ Тпл=0,5-0,7
| Т/ Тпл>0,7
|
|
| 1,05-1,10
1,10-1,22
1,16-1,34
| 1,10-1,15
1,22-1,32
1,34-1,52
| 1,15-1,30
1,32-1,70
1,52-2,20
| 1,30-1,50
1,70-2,25
2,20-3,40
|
| При переході від швидкості ε=1х10-1с-1 до ударного навантаження
| 1,10-1,25
| 1,25-1,75
| 1,75-2,50
| 2,50-3,50
|
| П р и м і т к а. Т - абсолютна температура деформації; Тпл – абсолютна температура плавлення.
|
Вплив масштабу враховують масштабним, або об'ємним, коефіцієнтом φ0. За даними С. І. Губкіна, при збільшенні об'єму, що деформується, з 25 до 25·103 см3 коефіцієнт φ0 зменшується від 1 до 0,4. Е. Н. Мошнін і Н. М. Золотухін для внесення поправки до розрахункових значень тисків, деформуючих сил і робіт при гарячому осаджуванні сталевих зливків рекомендують значення коефіцієнта φ0, приведені в табл. 4.3.
Таблиця 4.3 Значення φ0
| Маса злитка, т
φ0
| 0,5
0,80
| 6,0
0,70
|
0,60
|
0,55
|
0,50
|
Для врахування швидкісного і об'ємного чинників потрібно дійсну напругу as у розрахункових формулах множити на коефіцієнти φс і φ0.
Як уже згадувалося, аби зберегти подібність фізико-механічних властивостей, доцільно виготовляти модель з матеріалу натури. Проте це не завжди зручно і можливо. Тому для виявлення загальних закономірностей процесів пластичного формозмінення часто матеріал моделі вибирають відмінним від матеріалу натури. При цьому стежать, аби криві зміцнення моделі і натури, побудовані в безрозмірних координатах σ/σТ- εЕ/σТ, були подібні.
Найбільш поширені в практиці моделювання процесів ОМТ такі матеріали, як Al, Pb і різні їх сплави. Інколи для якісного аналізу процесів використовують пластилін, але відмінність у властивостях реологій пластиліну і металів може в деяких випадках привести до помилкових результатів.
Для моделювання процесів гарячої обробки металів в лабораторних умовах рекомендується використовувати Рb. Він добре обробляється, пластичний, має низьку температуру рекристалізації. Вводячи в Рb невеликі кількості Sb (до 5%) і Те (до 0,5%), можна змінювати механічні характеристики модельного матеріалу в досить широких межах.
Добрі результати можна отримати, використовуючи як модельний матеріал Al, який при холодній обробці мало зміцнюється. Як приклад приведемо результати дослідної перевірки Ю. М. Чижіковим закону силової подібності при обтисканні алюмінієвих циліндрових зразків в кімнатній температурі без мастила і з мастилом; масштаб моделювання т змінювався в межах 1,5 ... 7,5.
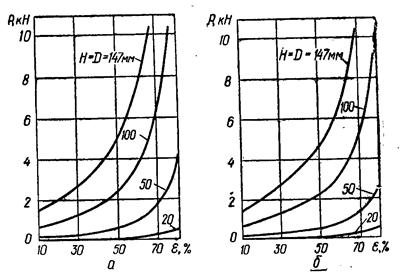
Рис.4.2 Залежність сили осадки Р від відносного обтискання ε алюмінієвих зразків: а - без мастила; б - з мастилом касторовою олією
Розміри зразків DхH при постійному відношенні D/H=1 змінювалися від 20x20 до 147x147 мм. Досліджено 4 типорозміру зразків з наступними масштабами т і показниками силової подібності т2:
m1 = 50/20 = 2,5; m12 = 6,25;
m2 = 100/20 = 5,0; m22 = 25;
m3 = 147/20 = 7,35; m32 = 54;
m4 = 100/50 = 2; m42 = 4;
m5 = 147/50 = 2,94; m52 = 8',65;
m6= 147/100=1,47; m62 = 2,16.
Зразки піддавали ступінчастому осаджуванню з кроком 10% відносного обтискання ε і постійною швидкістю 0,2 мм/с. Відповідно до закону подібності сила Р2 при деформації тіла великих розмірів (натури):
Р2 = m2 Р1, (4.29)
де Р1 - сила при деформації тіла менших розмірів (моделі).
Залежності сили осадки Р від відносного обтискання ε (рис.4.2) при деформації як без мастила, так і з мастилом і відношення сил, тобто значення показників подібності, отримані по цих графіках, переконливо показують, що при осіданні зразків з масштабом моделювання 1,5 ... 7,5 закон силової подібності (4.29) виконується з достатньою для практики точністю.


