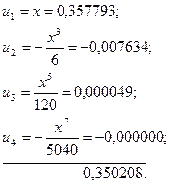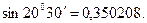Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Обчислення значень тригонометричних функційДата додавання: 2015-01-16; переглядів: 1464.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| ||||||||||||||||

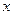 можна укласти у відрізок
можна укласти у відрізок 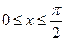 . Якщо
. Якщо 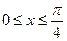 , то маємо:
, то маємо: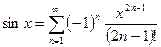 , (1)
, (1)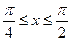 , то покладемо
, то покладемо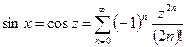 , (2)
, (2)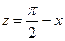 й
й 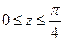 .
.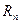 справедлива оцінка
справедлива оцінка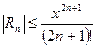 и.
и. 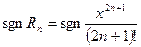
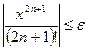 ,
,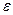 - задана залишкова похибка.
- задана залишкова похибка.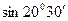 з точністю до
з точністю до 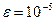 .
.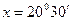 в радіани. Маємо:
в радіани. Маємо: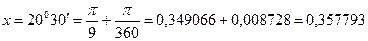 .
.