Для експонентної функції 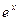 справедливий розклад
справедливий розклад
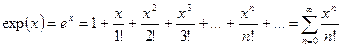 , (1)
, (1)
інтервал збіжності якого 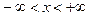 .
.
Залишковий член ряду (1) має вигляд
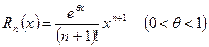 . (2)
. (2)
При більших по модулю значеннях 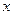 ряд (1) мало придатний для обчислень. Тому звичайно діють у такий спосіб: нехай
ряд (1) мало придатний для обчислень. Тому звичайно діють у такий спосіб: нехай
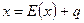 ,
,
де 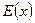 — ціла частина числа
— ціла частина числа 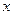 та
та 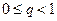 — дробова частина його.
— дробова частина його.
Маємо:
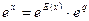 . (3)
. (3)
Перший множник добутку (3) може бути знайдений за допомогою множення:
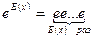 якщо
якщо 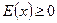 ,
,
або
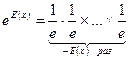 якщо
якщо 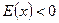 .
.
Тут
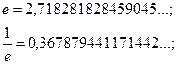
причому 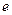 або
або 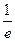 , для забезпечення заданої точності, варто взяти з досить великим числом десяткових знаків (у наш час число
, для забезпечення заданої точності, варто взяти з досить великим числом десяткових знаків (у наш час число 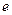 визначене з понад 300 десятковими знаками).
визначене з понад 300 десятковими знаками).
Що стосується другого множника 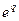 добутку (3), то для обчислення його користуються наведеним вище розкладом
добутку (3), то для обчислення його користуються наведеним вище розкладом
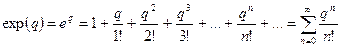 , (4)
, (4)
який при 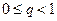 утворює швидко збіжний ряд, тому що на підставі формули (2) для залишкового члена
утворює швидко збіжний ряд, тому що на підставі формули (2) для залишкового члена 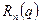 маємо оцінку
маємо оцінку
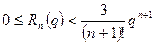 . (5)
. (5)
Можна вивести (спробуйте це зробити самостійно) більш точну формулу для оцінки залишку 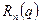 при
при 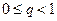 :
:
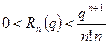 . (6)
. (6)
Якщо похибка 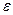 задана, то необхідне число членів
задана, то необхідне число членів 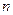 можна знайти підбором, розв’язуючи нерівність
можна знайти підбором, розв’язуючи нерівність
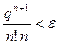 .
.
Можна довести, що якщо 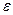 — задана припустима залишкова похибка й
— задана припустима залишкова похибка й 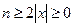 , то процес підсумовування варто припинити, як тільки буде виконана нерівність
, то процес підсумовування варто припинити, як тільки буде виконана нерівність
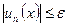 ,
,
де 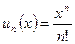 .
.
Іншими словами, процес підсумовування припиняється, якщо останній обчислений член 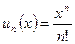 по модулю не перевищує
по модулю не перевищує 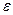 , при цьому
, при цьому
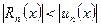 .
.
Приклад 1. Знайти 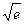 з точністю до
з точністю до 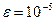 .
.
Розв’язок.
Послідовно маємо:
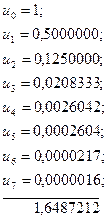
Округляючи суму до п'яти десяткових знаків після коми, одержимо:
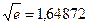 , (10)
, (10)
з похибкою 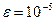 .
.
Для обчислення значень загальної показової функції 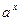 (
( 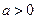 ) можна використати формулу
) можна використати формулу
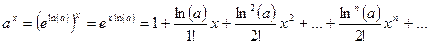 .
.


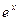 справедливий розклад
справедливий розклад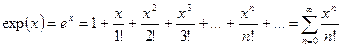 , (1)
, (1)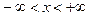 .
.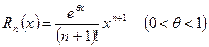 . (2)
. (2)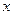 ряд (1) мало придатний для обчислень. Тому звичайно діють у такий спосіб: нехай
ряд (1) мало придатний для обчислень. Тому звичайно діють у такий спосіб: нехай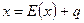 ,
,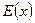 — ціла частина числа
— ціла частина числа 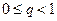 — дробова частина його.
— дробова частина його.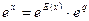 . (3)
. (3)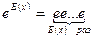 якщо
якщо 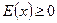 ,
,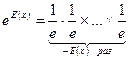 якщо
якщо 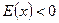 .
.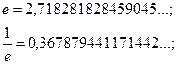
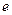 або
або 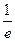 , для забезпечення заданої точності, варто взяти з досить великим числом десяткових знаків (у наш час число
, для забезпечення заданої точності, варто взяти з досить великим числом десяткових знаків (у наш час число 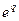 добутку (3), то для обчислення його користуються наведеним вище розкладом
добутку (3), то для обчислення його користуються наведеним вище розкладом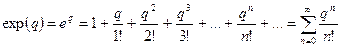 , (4)
, (4)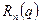 маємо оцінку
маємо оцінку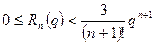 . (5)
. (5)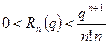 . (6)
. (6)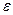 задана, то необхідне число членів
задана, то необхідне число членів 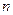 можна знайти підбором, розв’язуючи нерівність
можна знайти підбором, розв’язуючи нерівність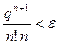 .
.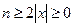 , то процес підсумовування варто припинити, як тільки буде виконана нерівність
, то процес підсумовування варто припинити, як тільки буде виконана нерівність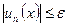 ,
,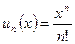 .
.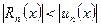 .
.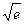 з точністю до
з точністю до 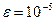 .
.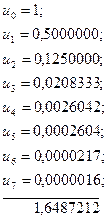
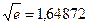 , (10)
, (10)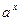 (
( 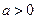 ) можна використати формулу
) можна використати формулу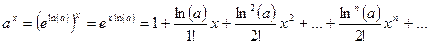 .
.