Мови програмуванняВідео уроки php mysqlПаскальСіАсемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux
Unix
Алгоритмічні мови
Архітектура мікроконтролерів
Введення в розробку розподілених інформаційних систем
Дискретна математика
Інформаційне обслуговування користувачів
Інформація та моделювання в управлінні виробництвом
Комп'ютерна графіка
Лекції
|
Обчислення значень аналітичної функціїДата додавання: 2015-01-16; переглядів: 1295.
|
Онлайн система числення Калькулятор онлайн звичайний Науковий калькулятор онлайн
| ||||||||||||||||

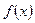 називається аналітичною в точці
називається аналітичною в точці 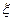 , якщо в деякому околі
, якщо в деякому околі 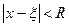 цієї точки функція розкладається в степеневий ряд (ряд Тейлора):
цієї точки функція розкладається в степеневий ряд (ряд Тейлора):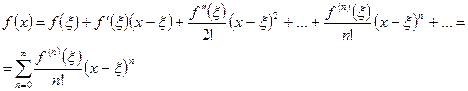 (1).
(1).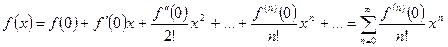 . (2)
. (2)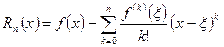
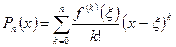 .
.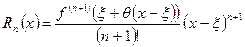 , (3)
, (3)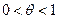 (грецька буква «тета»).
(грецька буква «тета»).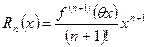 . (4)
. (4)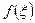 відомо й потрібно знайти значення
відомо й потрібно знайти значення 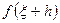 , де
, де 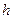 — «мале відхилення», то формулу (1) вигідно записувати у вигляді
— «мале відхилення», то формулу (1) вигідно записувати у вигляді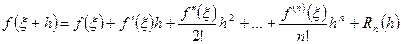 , (5)
, (5)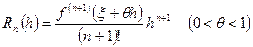 .
.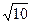 .
.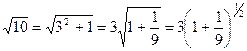 (6)
(6)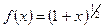 ,
,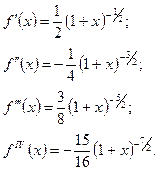
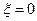 ,
, 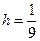 і з огляду на те, що
і з огляду на те, що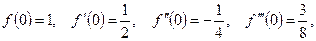
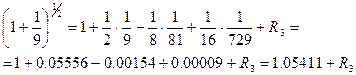 , (7)
, (7)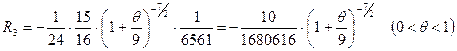 .
.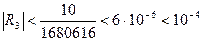 .
.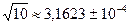 .
.