Із урахуванням (3.175) нерівності (3.173) набувають вигляду:
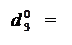
 1, якщо NA3П = 1 (NA3 =0);
1, якщо NA3П = 1 (NA3 =0);
0, якщо NA3П = 0 (NA3 = 1).
При діленні (-МА) DК на (-МВ)DК визначені нерівності можна пов’язати зі знаком NВ = 1. Тоді для d  отримаємо: :
отримаємо: :
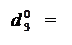
 1, якщо NA3П = NВ;
1, якщо NA3П = NВ;
0, якщо NA3П ≠ NВ.
Звідси дістанемо:
d  =
= 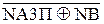 . (3.176)
. (3.176)
Алгоритм визначення позиції d  частки, очевидно, залежать від стану позиції d3 частки у попередньому циклі.
частки, очевидно, залежать від стану позиції d3 частки у попередньому циклі.
Спочатку побудуємо алгоритм визначення d  за d3 = 0. У цьому випадку початковий стан змінних після обчислення позиції d3 частки визна-чається рівняннями:
за d3 = 0. У цьому випадку початковий стан змінних після обчислення позиції d3 частки визна-чається рівняннями:
А3П(d3 = 0) = (-А3) = -(-МА3) = (+МА3); (3.177)
ВР2 = -МВР2, (3.178)
де А3П = (-А3) = -(МА – МВР3) = МВР3 – МА; ВР2 = (ВР3/2).
За вказаних умов (D>0) маємо:
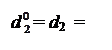
 1, якщо А2 > 0;
1, якщо А2 > 0;
0, якщо А2< 0, (3.179)
де А2 = (МА – МВР2), (3.180)
Із урахуванням (3.177) – (3.178) перетворимо (3.179), записавши його у вигляді:
А2(d3 = 0) = МА – МВР2 = (-АЗП) + МВР3 – МВР2 =
= (-АЗП) + МВР2 = (-АЗП) - (– МВР2) = (-АЗП) - ВР2.
Таким чином, залишок діленого для визначення позиції d2 частки можна полічити наступним чином:
А2П(d3 = 0) = (-А2) = А3П + ВР2.
Звідси дістанемо:
А2П  (d3 = 0) = (А3П
(d3 = 0) = (А3П  + ВР2
+ ВР2  )m128, (3.181)
)m128, (3.181)
де А3П  (d3 = 0) = (+МА3)
(d3 = 0) = (+МА3)  ; ВР2
; ВР2  =(-МВР2)
=(-МВР2)  ; NA2П =
; NA2П = 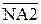 .
.
Отже, згідно з (3.179) і (3.181) маємо:
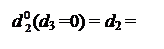
 1, якщо NA2П =
1, якщо NA2П = 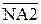 = 1;
= 1;
0, якщо NA2П = 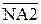 = 0.
= 0.
Із урахуванням знака дільника (NВ=1) нерівності можна подати у вигляді:
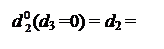
 1, якщо NA2П = NВ;
1, якщо NA2П = NВ;
0, якщо NA2П ≠ NВ.
Звідси дістанемо:
d  (d3 =0) =
(d3 =0) = 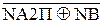 . (3.182)
. (3.182)
Якщо найстарша позиція частки d3 = 1, то початковий стан аргументів для визначення позиції d  частки описується змінними:
частки описується змінними:
А3П = (-А3) = (-МА3); (3.183)
ВР2 = (+МВР2), (3.184)
де МА3 = МА – МВР3; МВР2 = (МВР3/2).
При діленні (-МА) DК на (-МВ)DК знак частки ND = 0, тому згідно з (3.66) позиція d2 частки визначається нерівностями виду:
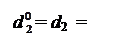
 1, якщо А2 > 0;
1, якщо А2 > 0;
0, якщо А2 < 0, (3.185)
де А2(d3 = 1) = (МА3 – МВР2). (3.186)
Із урахуванням (3.183) – (3.184) перетворимо (3.186) наступним чином:
А2П(d3 = 1)= - (МА3 – МВР2) = (-МА3) + МВР2 =
= А3П – (-МВР2) = А3П – ВР2.
Звідси дістанемо:
А2П  (d3 = 1) = (А3П
(d3 = 1) = (А3П  +
+ 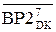 + 1)m128, (3.187)
+ 1)m128, (3.187)
де А3П  (d3 = 1) = (+МА3)
(d3 = 1) = (+МА3)  ; ВР2
; ВР2  =(-МВР2)
=(-МВР2)  ;
;
( 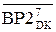 +1) = (+МВР2)
+1) = (+МВР2)  .
.
Згідно з властивостями доповняльного коду маємо:
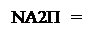
 1, якщо А2 > 0;
1, якщо А2 > 0;
0, якщо А2 < 0.
Тодінерівності (3.185) можна подати наступним чином:
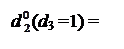
 1, якщо NA2П = 1 (NA2=0);
1, якщо NA2П = 1 (NA2=0);
0, якщо NA2П = 0 (NA2=1).
При діленні (-МА) DК на (-МВ)DК знак дільника NВ=1, тому нерівності можна пов’язати зі знаком NВ співвідношеннями:
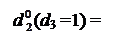
 1, якщо NA2П = NВ;
1, якщо NA2П = NВ;
0, якщо NA2П ≠ NВ.
Звідси дістанемо:
d  (d3 =1) =
(d3 =1) = 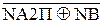 . (3.188)
. (3.188)
Узагальнюючи (3.181), (3.187), (3.182) і (3.188), маємо:
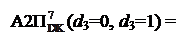
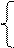 (А3П
(А3П  + BP2
+ BP2  ]m128, якщо NA3П ≠ NB;
]m128, якщо NA3П ≠ NB;
(А3П  +
+ 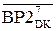 +1]m128, якщо NA3П=NB. (3.189)
+1]m128, якщо NA3П=NB. (3.189)
d 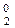 (d3=0, d3=1)=
(d3=0, d3=1)= 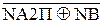 (3.190)
(3.190)
Залежності (3.189)–(3.190) ідентичні відповідним залежностям за другими комбінаціями знаків діленого і дільника, але ділення чисел (-МА) DК на (-МВ)DК за алгоритмами (3.189 – 3.190) має певні відмінності за умови, коли підсумкова остача С=0. Розглянемо докладно ці відмінності.
Очевидно, що у загальному випадку при діленні (-МА)DК на (-МВ)DК слушна остача має нульове значення, якщо
МА = МВ * MD,
де MD= (000 ÷ 111) - можливий рядок цифр модуля частки.
У цьому випадку змінні операції ділення у розгорнутому запису пов’я-зані співвідношенням:
(-МА) = (+МD) × (-МВ) = -(МВ×22× d3 + МВ×21× d2 + МВ× d1),
де d3d2d1 = (000 ÷ 111) – цифрові розряди модуля частки MD.
У випадку, коли d3d2d1 = 100, очевидно, часткові залишки діленого набувають значень:
А3 = - (МА - МВ×22) = МВ×21 ×d2 + МВ×d1 = МВ×21 ×0 + МВ×0 = 0;
А2 = - (МА - МВ×22 - МВ×21) = - (0 - МВ×21 ) = (+МВ);
А1 = - (МА - МВ×22 - МВ×21 ×d2 – МВ) =
= - (МА - МВ×22 - МВ×21×0 –МВ) =(+МВ).
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА)DК = (-4МВ)DК на (-МВ)DК дістанемо:
А3П = 0; А2П < 0; А1П < 0;
d 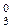 =
= 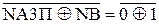 = 0 ;
= 0 ;
d  =
= 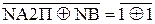 = 1;
= 1;
d  =
= 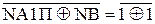 = 1.
= 1.
Таким чином, за визначеним загальним комп’ютерним алгоритмом ділення (-МА)DК=(-4МВ)DК на (-МВ)DК цифрова частина частки утворює код:
d  d
d  d
d  = 011 =
= 011 = 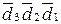 (за d3d2d1 = 100),
(за d3d2d1 = 100),
де d3d2d1 – цифрові розряди коректного підсумкового модуля додатної частки (MD = 100).
Звідси дістанемо:
MD(3/1) = d3d2d1 = 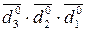 = 111 - d
= 111 - d  d
d  d
d  =
=
= 011 + 011 + 1 - d  d
d  d
d  = 011+(011 - d
= 011+(011 - d  d
d  d
d  ) +1 =
) +1 =
= 011 + (011 - 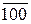 )+1 = 011 + (011 – 011) + 1 =
)+1 = 011 + (011 – 011) + 1 =
= 011 + 1 = ( 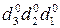 + 1).
+ 1).
Якщо модуль частки MD=d310 (MD = 010/110), то часткові залишки діленого (за С = 0) набувають значень:
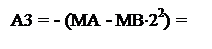
 < 0 при d3 = 0;
< 0 при d3 = 0;
> 0 при d3 = 1;
А2 = - (МА - МВ×22 - МВ×21) = МВ×20× d1 = МВ×20× 0 = 0;
А1 = - (МА - МВ×22×d3 - МВ×22 ×d2 – МВ) =
= - (МА - МВ×22×d3 - МВ×21×1 –МВ) =-(0 – МВ) = (+МВ).
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА)DК =- (d310×МВ)DК на (-МВ)DК дістанемо:
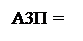
 > 0 при d3 = 0;
> 0 при d3 = 0;
< 0 при d3 = 1;
А2П = 0; А1П < 0;

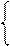
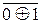 = 0 при d3 = 0;
= 0 при d3 = 0;
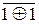 = 1 при d3 = 1;
= 1 при d3 = 1;
d  =
= 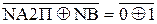 = 0;
= 0;
d  =
= 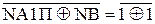 = 1.
= 1.
З цих міркувань випливає, що за визначеним загальним комп’ютерним алгоритмом ділення (-МА)DК на (-МВ)DК за MD = d310 цифрова частина частки утворює код:
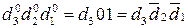 .
.
Отже, підсумковий стан додатної частки у цьому разі припустимо обчислювати за формулою:
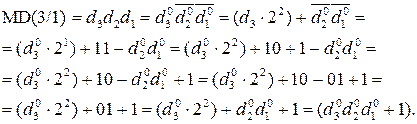
У разі, якщо МD=d3d21 (001/011/101/111), часткові залишки діленого згідно із загальною формулою набувають значень:
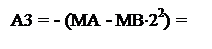
 < 0 за d3 = 0;
< 0 за d3 = 0;
> 0 за d3 = 1;
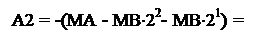
 < 0 за d2 = 0;
< 0 за d2 = 0;
> 0 за d2 = 1;
А1 = - (МА - МВ×22 - МВ×21 – МВ) = 0.
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА)DК на (-МВ)DК у цьому випадку отримаємо:
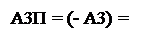
 > 0 за d3 = 0;
> 0 за d3 = 0;
< 0 за d3 = 1;
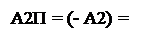
 > 0 за d2 = 0;
> 0 за d2 = 0;
< 0 за d2 = 1;
А1П = (- А1) = 0;

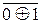 = 0 за d3 = 0;
= 0 за d3 = 0;
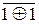 = 1 за d3 = 1;
= 1 за d3 = 1;
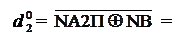
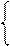
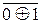 = 0 за d2 = 0;
= 0 за d2 = 0;
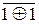 = 1 за d2 = 1;
= 1 за d2 = 1;
d  =
= 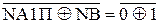 = 0 за d1 = 1.
= 0 за d1 = 1.
Таким чином, за визначеним загальним комп’ютерним алгоритмом ділення (МА)DК на (-МВ)DК утворюється код, який пов’язаний із підсумковою додатною часткою співвідношеннями:
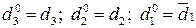 .
.
Отже, підсумкове значення додатної частки припустимо обчислювати за співвідношенням:
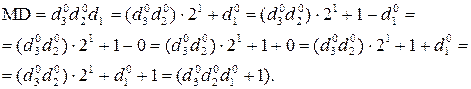
Таким чином, якщо рядок обчислювальних цифрових розрядів частки 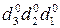 від ділення (-МА)DК на (-МВ)DК є відомим і підсумкова остача ділено-го має нульове значення, то загальна формула, за якою повинно визначатися істинне значення модуля додатної частки d3d2d1, має вигляд:
від ділення (-МА)DК на (-МВ)DК є відомим і підсумкова остача ділено-го має нульове значення, то загальна формула, за якою повинно визначатися істинне значення модуля додатної частки d3d2d1, має вигляд:
MD = d3d2d1 = d  d
d  d
d  + 1.
+ 1.
Узагальнюючи алгоритм ділення (-МА)DК на (-МВ)DК маємо:
0 
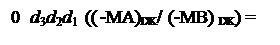 d
d  d
d  d
d  , якщо С ≠ 0;
, якщо С ≠ 0;
0  d
d  d
d  d
d  +1, якщо С = 0.
+1, якщо С = 0.
Виявлення нульового стану остачі в операції ділення ( - МА )DК на (-МВ)DК, за якою виконується виправлення (корекція) обчислених розрядів додатної частки, звичайно виконується шляхом контролю останнього залиш-ку А1П, який згідно з приведених міркувань пов'язаний з нульовою остачею ділення співвідношенням:
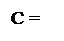
 0, якщо А1П = 0;
0, якщо А1П = 0;
0, якщо А1П = (+МВ).
Таким чином, нульовий стан остачі при діленні (-МА)DК на (-МВ)DК припустимо визначати за співвідношеннями:
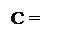
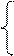 0, якщо А1П = 0;
0, якщо А1П = 0;
0, якщо А0 = 0;
(≠0), якщо А0 ≠ 0,
де А0 = [А1П + (-МВ)] - (3.191)
- пробний числовий код залишку діленого для виявлення нульового стану остачі від ділення (-МА) на (-МВ) за А1П < 0.
Зазначимо, що за А0 ≠ 0 залишок А1П < 0 являє собою істинний код підсумкової остачі ділення (-МА)DК на (-МВ)DК, тому за А0 ≠ 0 змінна А1П повинна відновлюватися за формулою:
А1П = А0 + (+МВ). (3.192)
Для визначення підсумкової остачі у загальному випадку розглянемо взаємозв’язок між (-МА), (-МВ), (+МD) і остачею С:
(-МА) = (-МВ) × МD + С.
Звідси дістанемо:
С = (-МА) + МВ × МD = (-МА – МВ × МD) =
= -(МА – МВ×22× d3 + МВ×21× d2 + МВ× d1),
де С = (МА - МВ × МD) – модуль від’ємної остачі С < 0 (NC=NA=1).
Отже, код остачі можна визначити за співвідношеннями:
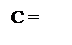
 -(МА - МВ×22×d3 - МВ×21×d2 + МВ), якщо d1 = 1; -(МА -МВ×22×d3 - МВ×21×d2), якщо d1 = 0.
-(МА - МВ×22×d3 - МВ×21×d2 + МВ), якщо d1 = 1; -(МА -МВ×22×d3 - МВ×21×d2), якщо d1 = 0.
Залишок діленого в останньому циклі за визначеним загальним комп’ютерним алгоритмом ділення (-МА)DК на (-МВ)DК обчислюється за формулою:
А1П = (-А1) = -(МА - МВ×22×d3 - МВ×21×d2 - МВ).
Звідси випливає, що істинне значення остачі С можна пов’язати з останнім залишком діленого А1П співвідношеннями:
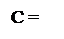
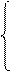 А1П, якщо d
А1П, якщо d  =d1=1 (тобто NA1П=NB i NA1П=NA); А1П+(-MB), якщо d
=d1=1 (тобто NA1П=NB i NA1П=NA); А1П+(-MB), якщо d  =d1=0
=d1=0
(тобто NA1П≠NB i NA1П≠NA);
Звідси дістанемо:
 А1П
А1П 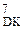 , якщо NA1П=(NB Å ND);
, якщо NA1П=(NB Å ND);
(А1П 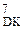 + ВР
+ ВР 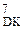 )m128, якщо NA1П≠ (NB Å ND),
)m128, якщо NA1П≠ (NB Å ND),
де NB Å ND = NA – первинний знак діленого А 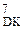 ;
;
ВР 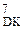 =(-МВ)
=(-МВ) 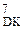 - доповняльний код розширеного формату дільника в останньому циклі.
- доповняльний код розширеного формату дільника в останньому циклі.
Приклади ділення (-МА)DK на (-МВ)DK на основі побудованих правил за алгоритмами “ а ” i “б” подано на рис.3.36 – 3.39.


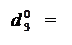
 1, якщо NA3П = 1 (NA3 =0);
1, якщо NA3П = 1 (NA3 =0); отримаємо: :
отримаємо: :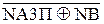 . (3.176)
. (3.176) частки, очевидно, залежать від стану позиції d3 частки у попередньому циклі.
частки, очевидно, залежать від стану позиції d3 частки у попередньому циклі.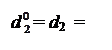
 (d3 = 0) = (А3П
(d3 = 0) = (А3П 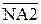 .
.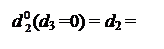
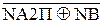 . (3.182)
. (3.182)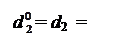
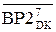 + 1)m128, (3.187)
+ 1)m128, (3.187)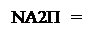
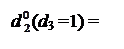
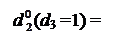
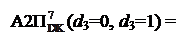
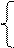 (А3П
(А3П 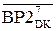 +1]m128, якщо NA3П=NB. (3.189)
+1]m128, якщо NA3П=NB. (3.189)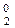 (d3=0, d3=1)=
(d3=0, d3=1)= 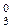 =
= 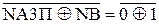 = 0 ;
= 0 ;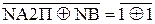 = 1;
= 1; =
= 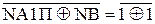 = 1.
= 1.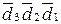 (за d3d2d1 = 100),
(за d3d2d1 = 100),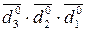 = 111 - d
= 111 - d  ) +1 =
) +1 = )+1 = 011 + (011 – 011) + 1 =
)+1 = 011 + (011 – 011) + 1 =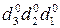 + 1).
+ 1).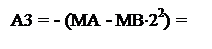

 = 0 при d3 = 0;
= 0 при d3 = 0;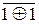 = 1 при d3 = 1;
= 1 при d3 = 1;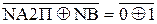 = 0;
= 0;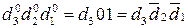 .
.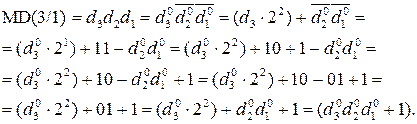
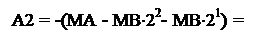
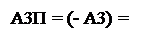
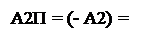
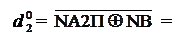
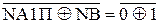 = 0 за d1 = 1.
= 0 за d1 = 1.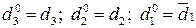 .
.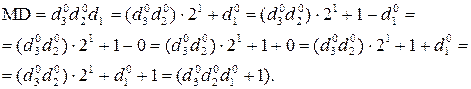
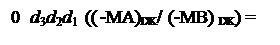 d
d  d
d 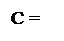
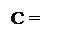
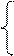 0, якщо А1П = 0;
0, якщо А1П = 0;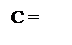
 А1П, якщо d
А1П, якщо d 
 А1П
А1П 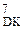 , якщо NA1П=(NB Å ND);
, якщо NA1П=(NB Å ND); DР
DР 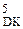
 А
А  ВP
ВP  X X X X X
X X X X X


 ND
ND 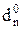 X X X 0 0
X X X 0 0

 ND
ND 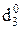
 X X 0 0 0
X X 0 0 0


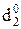


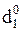
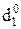 = NA1ПÅNB = 0
= NA1ПÅNB = 0

 0 0 0 1 0
D
0 0 0 1 0
D 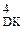
 1 1 1 0 0 1 1
1 1 1 0 0 1 1

 NA
NA


 0 0 0 0 1 1 1
0 0 0 0 1 1 1

 NA2П
NA2П




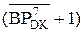 =
= 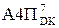
 BP
BP

 NB ≠ NA4П
NB ≠ NA4П 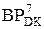 =
= 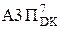
 BP
1 1 1 0 1 1 0
BP
1 1 1 0 1 1 0
 NB≠NA3П
NB≠NA3П 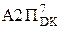
 1 1 1 1 0 1 1
NB=NA2П
1 1 1 1 0 1 1
NB=NA2П  =
= 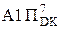 NA1П≠NА=(NDÅNB)
NA1П≠NА=(NDÅNB)
 NB≠NA1П
NB≠NA1П