Рисунок 3.32 – Приклад ділення (-МА)DК на (+МВ)DК
за алгоритмом «б» (при С = 0)
Рисунок 3.33 – Приклад ділення (-МА) DК на (+МВ)DК
за алгоритмом «а» (при С ≠ 0)
Звідси згідно з (3.164) – (3.165) дістанемо:
(А4П)  = (128 + А - ВР)m128 =(A
= (128 + А - ВР)m128 =(A  +
+ 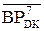 +1) m128 (3.168)
+1) m128 (3.168)
де A  = (-МА)
= (-МА)  ; BP
; BP  = (-МBP)
= (-МBP)  ; (
; ( 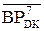 +1)
+1)  = (+МBP)
= (+МBP)  .
.
Згідно з властивостями доповняльного коду маємо:
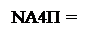
 NА4, якщо А4П = 0;
NА4, якщо А4П = 0;
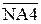 , якщо А4П ≠ 0. (3.169)
, якщо А4П ≠ 0. (3.169)
Тоді згідно з (3.169) співвідношення (3.166) набуває вигляду:
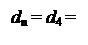
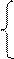 1, якщо А4П = 0 (при NА4П = NА4 = 0);
1, якщо А4П = 0 (при NА4П = NА4 = 0);
1, якщо NА4П = 1 (NА4 = 0 і А4П ≠ 0);
0, якщо NА4 = 0 (NА4 = 1 і А4П ≠ 0).
Таким чином, при діленні (-МА)DК на (-МВ)DК ознака розширу частки може бути пов’язана зі знаком діленого NВ =1 нерівностями виду:
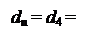

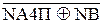 , якщо А4П ≠ 0;
, якщо А4П ≠ 0;
NА4П Å NВ, якщо А4П = 0.
Отже, згідно з (3.66) цифрова позиція d 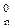 частки для визначення розря-ду переповнення розширеного формату частки визначається нерівностями виду:
частки для визначення розря-ду переповнення розширеного формату частки визначається нерівностями виду:
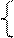
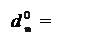 NА4П Å NВ, якщо А4П = 0;
NА4П Å NВ, якщо А4П = 0;
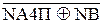 , якщо А4П ≠ 0. (3.170)
, якщо А4П ≠ 0. (3.170)
Приклади визначення позиції d 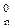 частки розширеного формату частки при діленні (-МА) DК на (-МВ)DК подано на рис.3.34 – 3.35.
частки розширеного формату частки при діленні (-МА) DК на (-МВ)DК подано на рис.3.34 – 3.35.
Рисунок 3.34 – Приклад визначення позиції 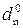 = 1 при
= 1 при
діленні (-МА) DK на (-МВ) DK (за залишком діленого А4П ≠ 0)
Припустімо, що визначення цифрової частини частки (d3d2d1) виконується зі зсувом вправо дільника В, тобто за алгоритмом «б».
Початкові змінні, за якими визначається наступна позиція d3 частки мають вигляд:
А4П = (-А4) = -(МА – МВР) = (+МА4); (3.171)
ВР3 = (-МВР3), (3.172)
де (+МА4) – додатковий залишок діленого;
ВР3 = (-МВР/2) = (-МВР3) – стан дільника після логічного зсуву на один біт вправо первинного розширеного формату дільника;
ВР = - МВР.
При діленні (-МА)DК на (-МВ)DК знак частки ND=0 і згідно з (3.66) справедливі співвідношення:
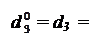
 1, якщо А3 > 0;
1, якщо А3 > 0;
0, якщо А3 < 0, (3.173)
де А3 = (МА – МВР3). (3.174)
Рисунок 3.35 – Приклад визначення позиції 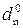 = 1 при
= 1 при
діленні (-МА)DK на (-МВ)DK (за залишком діленого А4П=0)
Із урахуванням (3.171) – (3.172) перетворимо (3.174), записавши його у вигляді:
А3 = МА – МВР3 = - А4П + МВР – МВР3 =
= - А4П + МВР – МВР/2 = -А4П + МВР3.
Звідси дістанемо:
АЗП = (-А3) = А4П – МВР3 = А4П + (-МВР3) = А4П + ВР3,
де АЗП = (-А3) – залишок діленого, протилежний залишку А3.
Таким чином, доповняльний код залишку АЗП визначається рівнянням:
А3П  = (А4П
= (А4П  + ВР
+ ВР  )m128, (3.175)
)m128, (3.175)
де АЗП = (-А3); А4П  = (+МА4)
= (+МА4)  ; ВР3
; ВР3  =(-МВР3)
=(-МВР3)  ;
;
NA3П = 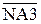 .
.


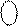 DР
DР 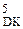
 А
А 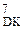
 В
В 


 ND
ND 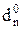 X X X 1 1
X X X 1 1

 ND
ND 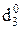
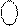
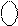 X X 1 1 1
X X 1 1 1

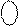
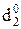
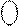
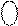

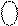
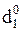
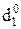 = NA1ПÅNB = 1
= NA1ПÅNB = 1
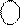
 ND=1=
ND=1=  1
1



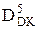 = (-0010)
= (-0010) 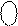 1 1 1 0 0 1 1
1 1 1 0 0 1 1
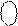

 NA
0 1 0 1
NA
0 1 0 1

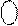

 0 0 0 1 1 1 0
0 0 0 1 1 1 0


 NA2П
NA2П 1 0 1 0 0 0
1 0 1 0 0 0 0 1 0 1
0 1 0 1
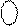
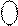

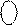
 1 1 1 1 1 0 1
1 1 1 1 1 0 1

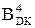 =
= 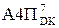
 = 2×
= 2× 
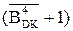 =
= 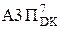
 = 2×
= 2× 
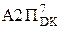
 = 2×
= 2×  =
= 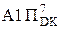 NB ≠ NA1П
NB ≠ NA1П

 = (128 + А - ВР)m128 =(A
= (128 + А - ВР)m128 =(A 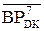 +1) m128 (3.168)
+1) m128 (3.168)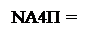
 NА4, якщо А4П = 0;
NА4, якщо А4П = 0;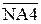 , якщо А4П ≠ 0. (3.169)
, якщо А4П ≠ 0. (3.169)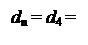
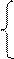 1, якщо А4П = 0 (при NА4П = NА4 = 0);
1, якщо А4П = 0 (при NА4П = NА4 = 0);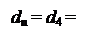
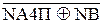 , якщо А4П ≠ 0;
, якщо А4П ≠ 0;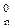 частки для визначення розря-ду переповнення розширеного формату частки визначається нерівностями виду:
частки для визначення розря-ду переповнення розширеного формату частки визначається нерівностями виду: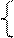
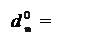 NА4П Å NВ, якщо А4П = 0;
NА4П Å NВ, якщо А4П = 0; DР
DР 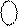 А
А 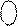 ВP
ВP 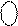 X X X X X
X X X X X

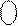
 ND
ND X X X X 0
X X X X 0
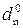
 X X X 0 1
X X X 0 1
 1 0 0 1 1 1 0
1 0 0 1 1 1 0

 NA
NA

 ND
ND




 NB=1
NB=1

 = NA4П Å NB =1
= NA4П Å NB =1


 NА = NВ
= A
NА = NВ
= A 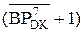 =
= 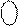
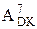 = 1 001 110
= 1 001 110
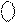
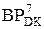 = 1011 000
= 1011 000
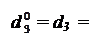
 А
А  ВP
ВP 
 ND
ND
 X X X X 0
ND = NAÅNB=0
X X X X 0
ND = NAÅNB=0





 NB=1
NB=1

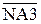 .
.