Розглянемо алгоритм ділення доповняльних кодів однакової довжини за наступними форматами аргументів і результату:
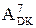 =(128 + А)m128;
=(128 + А)m128; 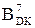 =(128 + B)m128;
=(128 + B)m128;
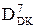 =(128 + D)m128;
=(128 + D)m128; 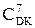 =(128 + C)m128;
=(128 + C)m128;
де А, В, D, С – відповідно знакові числові змінні діленого, дільника, частки та остачі.
Принцип визначення доповняльного коду частки при діленні допов-няльних кодів чисел однакового формату полягає в тому, що передусім обчислюють знак частки ND = (NAÅNB), який записується в усі розряди частки:
 D
D  = ND ND ND ND ND ND ND, тобто
= ND ND ND ND ND ND ND, тобто
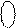
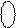 D
D  (ND=0) = 0 000 000 і D
(ND=0) = 0 000 000 і D  (ND=1) = 1 111 111.
(ND=1) = 1 111 111.
Рисунок 3.38 – Приклад ділення (-МА)DК на (-МВ)DК
за алгоритмом «б» при С ≠ 0 (А1П < 0, А0 ≠ 0)
Рисунок 3.39 – Приклад ділення (-МА) DК на (-МВ)DК
за алгоритмом «a» при С≠ 0 (А1П > 0).
Зазначимо, що за таким способом утворення початкового стану доповняльного коду частки при скороченій довжині значущої частини частки завжди забезпечується формування коректного підсумкового сполучення цифр у незначущих позиціях частки, які у доповняльному коді повинні мати нульові значення за ND = 0 і одиничні стани за ND = 1.
Як було визначено при діленні модулів чисел однакового формату, у загальному випадку значущі цифри частки D являють собою частку від ділення знормованого діленого АН на знормований дільник ВН, причому кількість значущих цифр цілої частини частки k пов’язана із кількістю незначущих цифр діленого А і дільника В співвідношенням:
k = (НВ +1) – НА,
де НВ, НА – кількість незначущих цифр у кодах дільника В і діленого А, які відкидаються у процесі формування знормованих станів дільника В 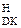 і діленого А
і діленого А 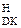 .
.
Слід зазначити також, що у випадку, коли НВ<НА, тобто за (НВ+1)–НА ≤ 0 і МА<МВ, модуль частки МD = 0. Тому, за (НВ+1) – НА≤ 0 операція ділення А 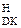 на В
на В 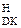 повинна блокуватися з онулюванням коду частки.
повинна блокуватися з онулюванням коду частки.
Лічба кількості значущих позицій у коді частки k звичайно виконується за допомогою реверсивного лічильника тактів (СТТ), який попередньо онулюється (СТТ=0). Різниця [(НВ+1) – НА ] визначається подачею на вхід
прямої лічби «+1» лічильника (НВ +1) сигналів, а потім на вхід зворотної лічби «-1» НА імпульсів. Зазначимо, що у процесі лічби змінної k відбу-вається блокування операції ділення, якщо числовий вираз поточного стану лічильника набуває нульового значення, тобто за СТТ = [(НВ + 1- НА)] = 0.
Кількість імпульсів НВ і НА на входах лічильника тактів СТТ фор-мується у процесі нормалізації доповняльних кодів дільника В  і діленого А
і діленого А  , яка виконується логічним зсувом вліво кожного із операндів до появи одиничного стану ознаки нормалізації відповідного доповняльного коду:
, яка виконується логічним зсувом вліво кожного із операндів до появи одиничного стану ознаки нормалізації відповідного доповняльного коду:
ПНВ = NВ Å ВН  (6); ПНА = NА Å АН
(6); ПНА = NА Å АН  (6), (3.195)
(6), (3.195)
де ПНВ, ПНА - ознака знормованого стану доповняльного коду відповідно дільника В  і діленого А
і діленого А  ;
;
NА, NВ – знакові розряди відповідно дільника В  і діленого А
і діленого А  ;
;
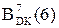 ,
, 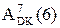 - поточний стан старших цифрових розрядів відповідно дільника і діленого.
- поточний стан старших цифрових розрядів відповідно дільника і діленого.
Значущі k цифр числової частини частки D  визначаються діленням знормованого доповняльного коду діленого АН
визначаються діленням знормованого доповняльного коду діленого АН  на знормований код діль-ника ВН
на знормований код діль-ника ВН  за будь-яким комп‘ютерним алгоритмом ділення доповняльних кодів. Сукупність операцій при нормуванні остачі операції ділення вико-нуються за правилами, які були визначені для операції ділення цілочислових модулів чисел однакового формату.
за будь-яким комп‘ютерним алгоритмом ділення доповняльних кодів. Сукупність операцій при нормуванні остачі операції ділення вико-нуються за правилами, які були визначені для операції ділення цілочислових модулів чисел однакового формату.
Приклади ділення цілочислових доповняльних кодів однакового формату А  на В
на В  за алгоритмами «б» і «а» подано на рис.3.40 – 3.41.
за алгоритмами «б» і «а» подано на рис.3.40 – 3.41.
Рисунок 3.40 – Приклад ділення A 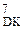 на В
на В 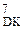 за алгоритмом «б»
за алгоритмом «б»
Вправи та запитання до розділу 3
1. Виконайте обчислення коефіцієнтів полінома частки:
МА = МВ*MD = MB(d4·23 + d3·22 + d2·21 + d1·20) =
= d4 (MB·23)+ d3 (MB·22)+ d2 (MB·21)+ d1 (MB·20),
де МА=100 011– модуль діленого подвійного (шестирозрядного) формату;
МВ = 111 – модуль дільника одинарного (трирозрядного) формату;
d4 – ознака переповнення гранично-припустимого формату модуля частки, обмеженого трирозрядним рядком цифр;
d3 d2 d1 – послідовність цифр цілої частини гранично–припустимого трирозрядного формату частки.
Вкажіть потрібну послідовність проміжних формул і дій. Порівняйте одержаний результат із правильною відповіддю.
Запропонуйте простий алгоритм і схему арифметичного пристрою для реалізації операції ділення МА(6/1) на МВ(3/1).
2. Згідно завдання 1 для визначення коефіцієнтів d3і d2 полінома-частки потрібно обчислити знак залишків діленого А3 і А2:
А3 = МА - d4 (MB·23) -(MB·22);
А2 = МА – dП (MB·23) - d3 (MB·22) - (MB·21).
Рисунок 3.41 – Приклад ділення A 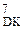 на В
на В 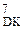 за алгоритмом «a»
за алгоритмом «a»
Як побудувати рекурентні функції, за якими залишок діленоно А2 був би пов'язаний з попереднім залишком А3 за d3 = 0 (А3<0) і d3 = 1 (А3≥0)? Який вигляд мають такі залежності за алгоритмоми «а» і «б» з відновленням і без відновлення залишку?
3. Знайдіть сукупність операцій, за допомогою яких можна знайти остачу МС(3/1) від ділення МА(6/1) на МВ(3/1):
МА = МВ * MD + MC = MB(d4·23 + d3·22 + d2·21 + d1·20) + MC,
де МА = 100110, МВ = 110; МС – модуль цілочислової остачі від ділення МА на МВ.
За допомогою яких операцій можна обчислити остачу МС(3/1) з використанням останнього залишку А1 за d1= 0 і d1= 1?
4. Обчисліть частку МD і остачу МС від ділення МА на МВ однакового формату:
МА(6/1) = МВ(6/1) * МD(6/1) + МС(6/1),
де МА(6/1) = 010001, МВ(6/1) = 000011.
Запропонуйте просту структуру арифметичного пристрою для ділення чисел однакового формату. Побудуйте функціональну мікропрограму роботи цієї структури.
5. Покажіть, як виконується ділення (±МА) 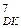 на (±МВ)
на (±МВ) 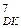 , якщо МА=100011 і МВ = 111, тобто остача МС=0.
, якщо МА=100011 і МВ = 111, тобто остача МС=0.
Запропонуйте загальний алгоритм визначення остачі 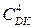 = 0.
= 0.
6. Найдіть частку та остачу від ділення (±МА) 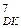 на (±МВ)
на (±МВ) 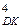 , якщо МА=100011 і МВ=110.
, якщо МА=100011 і МВ=110.
Запропонуйте загальний алгоритм визначення остачі 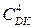 ≠ 0.
≠ 0.
7. Розробіть приклад ділення (±МА) 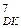 на (±МВ)
на (±МВ) 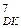 , якщо МА=010010 і МВ = 000011.
, якщо МА=010010 і МВ = 000011.
Запропонуйте загальний алгоритм визначення припустимої кількості значущих цифр частки.
8. Які випадки блокування процедури ділення (±МА) 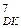 на (±МВ)
на (±МВ) 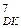 повинні фіксуватися за довільних величин операндів МА і МВ?
повинні фіксуватися за довільних величин операндів МА і МВ?
Наведіть приклади, за якими процедура ділення повинна перериватися.


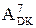 =(128 + А)m128;
=(128 + А)m128; 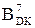 =(128 + B)m128;
=(128 + B)m128;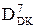 =(128 + D)m128;
=(128 + D)m128; 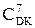 =(128 + C)m128;
=(128 + C)m128; D
D  = ND ND ND ND ND ND ND, тобто
= ND ND ND ND ND ND ND, тобто
 D
D  DР
DР 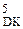
 А
А 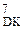
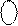 ВP
ВP  X X X X X
X X X X X


 ND
ND 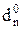 X X X 0 0
X X X 0 0
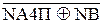 =0
ПП = NDÅ
=0
ПП = NDÅ 
 ND
ND 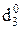
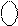 X X 0 0 0
X X 0 0 0


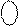
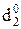
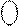
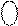
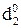 =
= 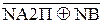 =1
=1
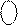

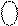
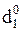

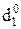 = NA1ПÅNB = 1
= NA1ПÅNB = 1
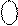

 0 0 0 1 1
D
0 0 0 1 1
D 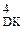
 1 1 1 0 0 0 0
1 1 1 0 0 0 0

 NA
0 1 0 1 0 0 0
NA
0 1 0 1 0 0 0

 0 0 1 1 0 0 0
0 0 1 1 0 0 0

 0 0 0 0 1 0 0
0 0 0 0 1 0 0

 NA2П
NA2П
 NA1П =(NDÅNB)=NА
NA1П =(NDÅNB)=NА
 1 1 1 1 1 1 1
1 1 1 1 1 1 1
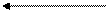
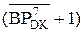 =
= 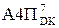
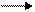 BP
BP

 NB ≠ NA4П (
NB ≠ NA4П ( 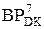 )
=
)
= 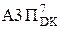
 BP
1 1 1 0 1 1 0
BP
1 1 1 0 1 1 0
 NB≠NA3П (
NB≠NA3П ( 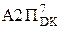
 1 1 1 1 0 1 1
NB=NA2П
1 1 1 1 0 1 1
NB=NA2П 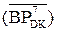
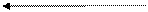 =
= 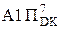 NA1П = NB
NA1П = NB

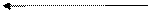

 відновлення залишку А1П
відновлення залишку А1П 

 0 1 1 0 1 1 0
0 1 1 0 1 1 0 1 0 1 1
1 0 1 1
 0 1 0 1
0 1 0 1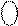 ≠(NDÅNB)=NА
≠(NDÅNB)=NА
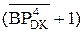 =
= 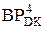 )
=
)
= 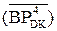

 NB≠NA1П (
NB≠NA1П ( 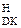 і діленого А
і діленого А 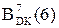 ,
, 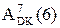 - поточний стан старших цифрових розрядів відповідно дільника і діленого.
- поточний стан старших цифрових розрядів відповідно дільника і діленого. D
D 

 А
А 

 В
В  7 6 5 4 3 2 1
7 6 5 4 3 2 1
 7 6 5 4 3 2 1
7 6 5 4 3 2 1
 ND = NAÅNB=1
ND = NAÅNB=1





 + 1
+ 1


 HA=2
HA=2
 0 0 0 1 1 0 0
0 0 0 1 1 0 0


 NA1
NA1


 NB
NB
 HB=3
HB=3
 1 0 1 1 0 0 0
BH2DK
1 0 1 1 0 0 0
BH2DK
 NB ≠ NA
= A2DK
NB ≠ NA
= A2DK
 BH2DK
BH2DK
 1 1 0 1 1 0 0
1 1 0 1 1 0 0 NB ≠ NA2
NB ≠ NA2
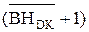


 ND
ND


 + 1
+ 1

 0 1 0 1 0 0 0
0 1 0 1 0 0 0
 BHDK
NB ≠ NA
= A2ПDK
BHDK
NB ≠ NA
= A2ПDK
 NB ≠ NA2П
NB ≠ NA2П NA1П ≠NBÅND=1
NA1П ≠NBÅND=1
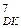 на (±МВ)
на (±МВ) 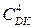 = 0.
= 0.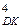 , якщо МА=100011 і МВ=110.
, якщо МА=100011 і МВ=110.