А3П = 0; А2П < 0; А1П < 0;
d 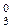 =
= 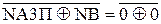 = 1 ;
= 1 ;
d  =
= 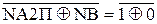 = 0;
= 0;
d  =
= 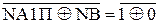 = 0.
= 0.
Таким чином, за визначеним загальним комп’ютерним алгоритмом при діленні (-МА)DK=(-4МВ)DK на (+МВ)DK (за С=0) цифрова частина частки d  d
d  d
d  =100, тобто складає слушний код цифрової частини доповняльного коду від’ємної частки (-100):
=100, тобто складає слушний код цифрової частини доповняльного коду від’ємної частки (-100):
d  d
d  d
d  = 100 = 011 + 1 =
= 100 = 011 + 1 =  + 1 =
+ 1 =
= 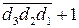 =
= 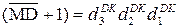 ,
,
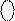 де
де 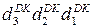 - цифрові розряди істинного значення доповняльного коду від’ємної частки D
- цифрові розряди істинного значення доповняльного коду від’ємної частки D 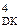 = 1
= 1 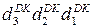 ((D = - d3d2d1= -100).
((D = - d3d2d1= -100).
Якщо модуль частки МD = d310 (МD = 010/110), то часткові залишки діленого (за С = 0) набувають значень:
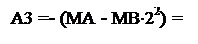
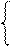 < 0 при d3 = 0;
< 0 при d3 = 0;
> 0 при d3 = 1;
А2 = - (МА - МВ×22 – МВ×21) = МВ×20× d1 = МВ×20×0 = 0;
А1 = - (МА - МВ×22× d3 - МВ×21× d2- МВ) =
= - (МА – МВ×22×d3 - МВ×21× 1 – МВ) = - (0 – МВ) = (+МВ).
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА)DK = - (d310*МВ)DK на (+МВ)DK дістанемо:
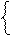
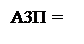 > 0 при d3 = 0;
> 0 при d3 = 0;
< 0 при d3 = 1;
А2П = 0; А1П < 0;

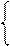
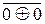 =1 при d3 = 0;
=1 при d3 = 0;
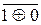 = 0 при d3 = 1;
= 0 при d3 = 1;
d  =
= 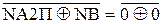 = 1;
= 1;
d  =
= 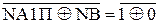 = 0.
= 0.
З цих міркувань випливає, що за визначеним загальним комп’ютерним алгоритмом ділення (-МА)DK=-(d310*МВ)DK на (+МВ)DK (за С=0) маємо відразу розшукуваний код цифрової частини від’ємної частки в доповняль-ному коді:
d  d
d  d
d  =
= 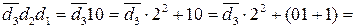
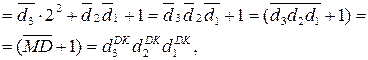
де 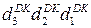 - підсумкова цифрова частина доповняльного коду від’єм-ної частки D = (- d3 1 0).
- підсумкова цифрова частина доповняльного коду від’єм-ної частки D = (- d3 1 0).
У разі, коли модуль частки МD(3/1) = d3d21 (001/011/101/111), часткові залишки при діленні (-МА) на (+МВ) набувають значень:
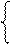
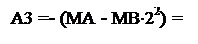 < 0 при d3 = 0;
< 0 при d3 = 0;
> 0 при d3 = 1;
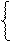
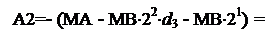 < 0 при d2 = 0;
< 0 при d2 = 0;
> 0 при d2 = 1;
А1 = - (МА - МВ×22× d3 - МВ×21× d2- МВ) = 0.
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА) DK на (+МВ) DK у цьому випадку маємо:
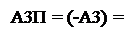
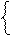 > 0 при d3 = 0;
> 0 при d3 = 0;
< 0 при d3 = 1;
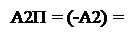
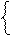 > 0 при d2 = 0;
> 0 при d2 = 0;
< 0 при d2 = 1;
А1П = (-А1) = 0;

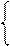
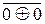 = 1 при d3 = 0;
= 1 при d3 = 0;
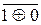 = 0 при d3 = 1;
= 0 при d3 = 1;
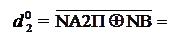
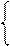
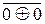 = 1 при d2 = 0;
= 1 при d2 = 0;
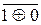 = 0 при d2 = 1;
= 0 при d2 = 1;
d  =
= 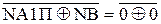 = 1 при d1 = 1 .
= 1 при d1 = 1 .
Узагальнюючи, маємо:
d  d
d  d
d 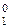 =
= 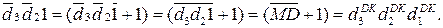
Таким чином, якщо значення цифрових розрядів частки d  d
d  d
d 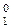 від ділення (-МА)DK на (+МВ)DK є відомими і підсумкова остача діленого дорів-нює нулю (С=0), то цифрова частина доповняльного кода частки
від ділення (-МА)DK на (+МВ)DK є відомими і підсумкова остача діленого дорів-нює нулю (С=0), то цифрова частина доповняльного кода частки 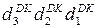 повністю збігається із обчисленими цифровими розрядами d
повністю збігається із обчисленими цифровими розрядами d  d
d  d
d 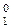 , тобто
, тобто
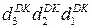 = d
= d  d
d  d
d 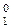 .
.
Узагальнюючи алгоритм ділення (-МА)DK на (+МВ)DK маємо:
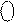
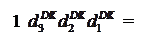
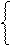
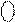 1 d
1 d  d
d  d
d 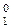 + 1, якщо С ≠ 0;
+ 1, якщо С ≠ 0;
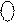 1 d
1 d  d
d  d
d 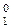 , якщо С = 0.
, якщо С = 0.
Виявлення нульового стану підсумкової остачі операції ділення (-МА)DK на (+МВ)DK, за якою не потрібно виконувати виправлення (корекцію) обчислених розрядів від’ємної частки, звичайно виконується шляхом контро-лю останнього часткового залишку діленого А1П, який згідно з вищеприве-дених міркувань, пов’язаний з нульовою остачею ділення співвідношенням:
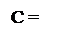
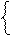 0, якщо А1П = 0;
0, якщо А1П = 0;
0, якщо А1П = (-МВ).
Таким чином, нульову остачу при діленні (-МА)DK на (+МВ)DK припус-тимо визначати за нерівностями:
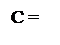
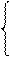 0, якщо А1П = 0;
0, якщо А1П = 0;
0, якщо А0 = 0;
(≠0), якщо А0 ≠ 0,
де А0 = [А1П + (+МВ)] - (3.163)
- пробний числовий код для виявлення нульового стану підсумкової остачі операції ділення за останнім істинним залишком діленого А1П<0.
Зазначимо, що за А0 ≠ 0 залишок А1П ≠ 0 являє собою правильне значення істинної остачі ділення (-МА)DK на (+МВ)DK , тому за А0≠0 А1П повинна відновлюватись за формулою:
А1П = А0 + (-МВ).
Побудуємо тепер загальний алгоритм визначення істинного значення від’ємної остачі при діленні (- МА)DK на (+МВ)DK.
У цьому випадку при діленні (- МА)DK на (+МВ)DK аргументи, частка і остача С ≠ 0 взаємопов’язані співвідношенням:
(-МА) = (+МВ)×(-МD) + С.
Звідси дістанемо:
С= (-МА) + МВ × МD = - (МА - МВ×22× d3 + МВ×21× d2 + МВ× d1),
де (МА - МВ × МD) – модуль від’ємної остачі С.
Таким чином, маємо:
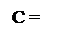
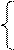 - (МА - МВ×22× d3 - МВ×21× d2 - МВ), якщо d1 = 1 (
- (МА - МВ×22× d3 - МВ×21× d2 - МВ), якщо d1 = 1 ( 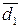 = 0);
= 0);
- (МА - МВ×22× d3 - МВ×21× d2), якщо d1 = 0 ( 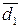 = 1).
= 1).
В останньому циклі операції ділення (-МА)DK на (+МВ)DK залишок діленого обчислюється за формулою:
А1П = - (МА - МВ×22× d3 - МВ×21× d2 - МВ).
Таким чином, остачу С можна пов’язати із залишком А1П співвідно-шеннями:
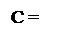
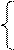 А1П, якщо d
А1П, якщо d 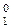 =
= 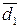 = 0 (тобто NA1П ≠ NВ і NA1П = NА);
= 0 (тобто NA1П ≠ NВ і NA1П = NА);
А1П+(-МВ), якщо d 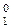 =
= 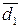 = 1 (тобто NA1П = NВ і NA1П ≠ NА).
= 1 (тобто NA1П = NВ і NA1П ≠ NА).
Отже, доповняльний код остачі слід обчислювати за співвідношеннями:
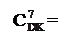
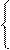 А1П
А1П  , якщо NA1П = (NВÅND);
, якщо NA1П = (NВÅND);
(А1П  +
+ 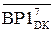 +1)m128, якщо NA1П ≠ (NВÅND) і (NA1П=NВ),
+1)m128, якщо NA1П ≠ (NВÅND) і (NA1П=NВ),
де (NВÅND) = NА – первинний знак діленого А DК;
ВР1  = (+ МВ)
= (+ МВ)  - доповняльний код розширеного формату дільника в останньому циклі.
- доповняльний код розширеного формату дільника в останньому циклі.
Приклади ділення (-МА)DК на (+МВ)DК на основі побудованих правил визначення доповняльного коду результату за алгоритмами “б” і “а” подано на рис.3.31 – 3.33.
Рисунок 3.31 – Приклад ділення (-МА) DК на (+МВ)DК
за алгоритмом «б» (при С ¹ 0)
Розглянемо тепер правила ділення (-МА) DК на (-МВ)DК .
За цих аргументів первинний код діленого і розширеного коду дільника визначаються змінними:
А = - МА; (3.164)
ВР = - МВР, (3.165)
де МА, МВР – відповідно модуль діленого А і модуль розширеного коду дільника В.
Розшир частки dn = d4 = 1 за цих умов виникає у тому випадку, коли МА ≥ МВР. Звідси маємо:
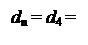
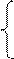 1, якщо А4 = 0;
1, якщо А4 = 0;
1, якщо А4 > 0 (А4 ≠0 );
0, якщо А4 < 0 (А4 ≠0 ), (3.166)
де А4 = (МА – МВР). (3.167)
Для визначення залишку діленого А4 в доповняльному коді перетвори-мо (3.167) наступним чином:
А4П = (-А4) = (-МА) - (-МВ) = А – ВР,
де А4П = (-А4) – залишок діленого, протилежний А4.


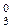 =
= 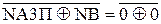 = 1 ;
= 1 ; =
= 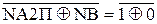 = 0;
= 0; =
= 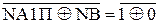 = 0.
= 0. d
d 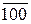 + 1 =
+ 1 =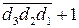 =
= 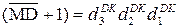 ,
,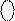 де
де 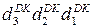 - цифрові розряди істинного значення доповняльного коду від’ємної частки D
- цифрові розряди істинного значення доповняльного коду від’ємної частки D 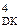 = 1
= 1 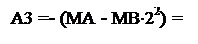
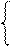 < 0 при d3 = 0;
< 0 при d3 = 0;
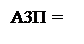 > 0 при d3 = 0;
> 0 при d3 = 0;
 =1 при d3 = 0;
=1 при d3 = 0;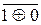 = 0 при d3 = 1;
= 0 при d3 = 1;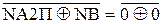 = 1;
= 1;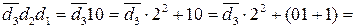
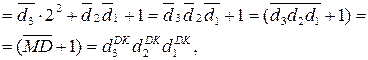
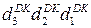 - підсумкова цифрова частина доповняльного коду від’єм-ної частки D = (- d3 1 0).
- підсумкова цифрова частина доповняльного коду від’єм-ної частки D = (- d3 1 0).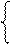
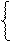
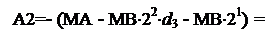 < 0 при d2 = 0;
< 0 при d2 = 0;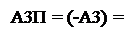
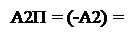
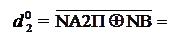
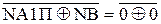 = 1 при d1 = 1 .
= 1 при d1 = 1 .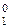 =
= 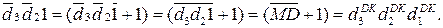
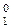 від ділення (-МА)DK на (+МВ)DK є відомими і підсумкова остача діленого дорів-нює нулю (С=0), то цифрова частина доповняльного кода частки
від ділення (-МА)DK на (+МВ)DK є відомими і підсумкова остача діленого дорів-нює нулю (С=0), то цифрова частина доповняльного кода частки 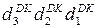 повністю збігається із обчисленими цифровими розрядами d
повністю збігається із обчисленими цифровими розрядами d 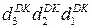 = d
= d 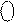
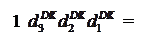
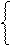
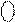 1 d
1 d 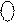 1 d
1 d 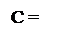
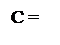
 0, якщо А1П = 0;
0, якщо А1П = 0;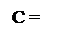
 - (МА - МВ×22× d3 - МВ×21× d2 - МВ), якщо d1 = 1 (
- (МА - МВ×22× d3 - МВ×21× d2 - МВ), якщо d1 = 1 ( 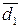 = 0);
= 0);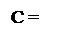
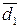 = 0 (тобто NA1П ≠ NВ і NA1П = NА);
= 0 (тобто NA1П ≠ NВ і NA1П = NА);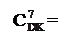
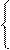 А1П
А1П  , якщо NA1П = (NВÅND);
, якщо NA1П = (NВÅND);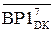 +1)m128, якщо NA1П ≠ (NВÅND) і (NA1П=NВ),
+1)m128, якщо NA1П ≠ (NВÅND) і (NA1П=NВ),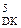
 X X X X X
X X X X X


 ND
ND 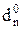 X X X 1 1
X X X 1 1

 ND
ND 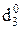
 X X 1 1 1
X X 1 1 1

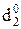

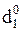

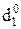 = NA1П ÅNB = 1
= NA1П ÅNB = 1

 ND 1
ND 1



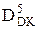 = (-0010)DK
= (-0010)DK 1 1 1 0 0 1 1
1 1 1 0 0 1 1

 NA
0 1 0 1 0 0 0
NA
0 1 0 1 0 0 0

 0 0 1 1 0 1 1
0 0 1 1 0 1 1

 0 0 0 0 1 1 1
0 0 0 0 1 1 1


 NA2П
NA2П 0 0 0 0 1 0 1
0 0 0 0 1 0 1


 (
( 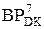 )
=
)
= 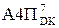
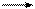 BP
BP
 NB = NA4П
NB = NA4П
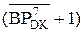 =
= 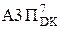
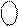
 BP
BP
 0 0 0 1 0 1 0
NB = NA3П
0 0 0 1 0 1 0
NB = NA3П
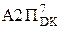

 0 0 0 0 1 0 1
NB ≠ NA2П
0 0 0 0 1 0 1
NB ≠ NA2П

 NB ¹ NA
NB ¹ NA
 (NA= ND Å NB)
(NA= ND Å NB)

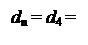
 1, якщо А4 = 0;
1, якщо А4 = 0; DР
DР 

 C=0 (ND=1)
C=0 (ND=1)
 +0
+0

 1 1 1 1 0 1 1
1 1 1 1 0 1 1 =
=  =
= 
 =
=  NB ≠ NA1П
NB ≠ NA1П

 = C
= C