Рисунок 3.27 – Приклад ділення (+МА) DК на (-МВ)DК за алгоритмом «a»
Через те, що при діленні (-МА)DК на (+МВ)DК частка має від’ємне значе-ння (ND=1), згідно із (3.66) розшир d 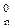 частки визначається за формулою:
частки визначається за формулою:
d 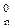 =
= 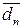 .
.
Узагальнюючи, маємо:
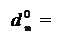
 NА4П ÅNB, якщо А4П = 0;
NА4П ÅNB, якщо А4П = 0;
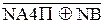 , якщо А4П ≠ 0. (3.143)
, якщо А4П ≠ 0. (3.143)
Приклади визначення позиції d 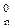 розширеного формату частки при діленні (-МА)DК на (+МВ)DК подано на рис.3.28-3.30.
розширеного формату частки при діленні (-МА)DК на (+МВ)DК подано на рис.3.28-3.30.
Рисунок 3.28 – Приклад визначення ознаки 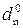 = 1 при
= 1 при
діленні (-МА)DK на (+МВ)DK (за залишком діленого А4П≠0)
Рисунок 3.29 – Приклад визначення ознаки 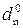 = 0 при
= 0 при
діленні (-МА)DK на (+МВ)DK (за залишком діленого А4П≠0)
Рисунок 3.30 – Приклад визначення 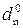 = 0 при діленні
= 0 при діленні
(-МА)DK на (+МВ)DK (за залишком діленого А4П=0)
Припустімо, що наступна цифра частки d 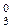 обчислюється зі зсувом дільника вправо, тобто за алгоритмом «б».
обчислюється зі зсувом дільника вправо, тобто за алгоритмом «б».
Початковий стан змінних, за яким визначається позиція d 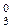 частки, має вигляд:
частки, має вигляд:
А4П = -(МА – МВР) = (+МА4); (3.144)
ВР3 = (+ МВР3) = (МВР/2), (3.145)
де (+МА4) – додатний модуль залишку А4П;
МВР3 = (+МВР/2) – стан дільника після логічного зсуву на один біт вправо розширеного подвійного модуля дільника МВР;
При діленні (-МА) на (+МВ) знак частки ND = 1, тому у загальному випадку згідно з (3.66) справедливі нерівності виду:
d 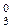 =
= 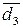 = 0, якщо А3 > 0, інакше d
= 0, якщо А3 > 0, інакше d 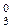 =
= 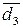 = 1, (3.146)
= 1, (3.146)
де А3 = (МА – МВ3). (3.147)
Із урахуванням (3.143) – (3.144) перетворимо (3.147), записавши його у вигляді:
А3 = МА – МВР3 = МВР – А4П – МВР3 = (-А4П) + МВР3.
Для обчислення залишку А3 у доповняльному коді перетворимо далі рівняння наступним чином:
А3П = (-А3) = А4П – ВР3,
де А3П = (-А3) – залишок діленого, протилежний залишку А3.
Звідси дістанемо:
А3П  = (А4П
= (А4П  +
+ 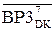 + 1)m128, (3.148)
+ 1)m128, (3.148)
де А4П  = (+МА4)
= (+МА4)  ; ВР3
; ВР3  = (+МВР3)
= (+МВР3)  ; NA3П =
; NA3П = 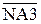 (за А3≠0).
(за А3≠0).
Із урахуванням (3.148) нерівності (3.146) набувають вигляду:
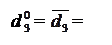
 0, якщо NA3П = 1;
0, якщо NA3П = 1;
1, якщо NA3П = 0.
При діленні (-МА)DK на (+МВ)DK знак дільника NB = 0, тому нерівності можна записати у вигляді:
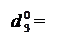
 0, якщо NA3П ≠ NВ;
0, якщо NA3П ≠ NВ;
1, якщо NA3П = NВ.
Звідси дістанемо:
d 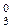 =
= 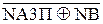 (3.149)
(3.149)
Алгоритм визначення наступної позиції d2 частки залежить від стану позиції d3 частки.
За d3=0 початковий стан сукупності числових змінних після обчислення позиції d3 частки визначається рівняннями:
А3П = (-А3) = -(-МА3) = (+МА3); (3.150)
ВР2= = (+МВР2), (3.151)
де АЗП = (-А3) = - (МА – МВР3) = МВР3 – МА;
МВР2 = (МВР3/2).
За визначених умов (ND = 1) маємо:
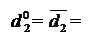
 0, якщо A2 > 0;
0, якщо A2 > 0;
1, якщо A2 < 0, (3.152)
де А2 = (МА – МВР2). (3.153)
Із урахуванням (3.150) – (3.151) перетворимо (3.153), записавши його у вигляді:
А2 = МА – МВР2 = (-А3П + МВР3) – МВР2 =
= (-А3П) + МВР2 = (-А3П) + ВР2.
Таким чином, залишок діленого для визначення позиції d2 частки можна полічити наступним чином:
А2П = (-А2) = (А3П – ВР2).
Отже, доповняльний код залишку А2П визначається співвідношенням:
А2П  = (А3П
= (А3П  +
+ 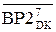 + 1)m128 (3.154)
+ 1)m128 (3.154)
де А3П  = (+МА3)
= (+МА3)  ; ВР2
; ВР2  = (+МВР2)
= (+МВР2)  .
.
Звідси з урахуванням (3.152) і (3.154), дістанемо:
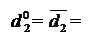
 0, якщо NA2П = 1 (NA2 = 0);
0, якщо NA2П = 1 (NA2 = 0);
1, якщо NA2П = 0 (NA2 = 1).
При діленні (-МА)DK на (+МВ)DK знак дільника NB = 0, тому нерівності можна записати у вигляді:
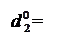
 0, якщо NA2П ≠ NВ;
0, якщо NA2П ≠ NВ;
1, якщо NA2П = NВ.
Звідси дістанемо:
d  ( d3 = 0) =
( d3 = 0) = 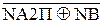 (3.155)
(3.155)
Якщо найстарша цифра частки d3 = 1, то первинний стан аргументів при визначені позиції d2 частки описується співвідношеннями:
А3(d3 = 1) = (+МА3); (3.156)
ВР2 = (+ МВР2), (3.157)
де МА3 = МА – МВР3; МВР2 = (МВР3/2).
При діленні (-МА)DK на (+МВ)DK частка має від’ємне значення (ND=1), тому згідно з (3.66) цифра d  частки повинна визначитися за нерівностями виду:
частки повинна визначитися за нерівностями виду:
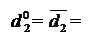
 0, якщо A2 > 0;
0, якщо A2 > 0;
1, якщо A2 < 0, (3.158)
де А2(d3 = 1) = МА3 – МВР2. (3.159)
Із урахуванням (3.156–3.157) перетворимо співвідношення (3.159) наступним чином:
А2(d3 = 1) = МА3 – МВР2 = (+МА3) – (+МВР2) = А3 – ВР2.
Звідси дістанемо:
А2П(d3 = 1) = (-А2) = (-А3) + ВР2 = (А3П + ВР2).
Таким чином, доповняльний код залишку А2П можна подати у формі:
А2П  (d3 = 1) = (А3П
(d3 = 1) = (А3П  + ВР2
+ ВР2  )m128,
)m128,
де А3П  (d3 = 1) = (-МА3)
(d3 = 1) = (-МА3)  ; ВР2
; ВР2  = (+МВР2)
= (+МВР2)  .
.
Згідно з властивостями доповняльного коду маємо:
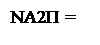
 1, якщо A2 > 0;
1, якщо A2 > 0;
0, якщо A2 < 0.
Звідси дістанемо:
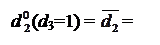
 1, якщо NA2П = 0 (A2 < 0);
1, якщо NA2П = 0 (A2 < 0);
0, якщо NA2П = 1 (A2 > 0).
При діленні (-МА)DK на (+МВ)DK нерівності можна пов’язати зі знаком дільника NB = 0 співвідношеннями:
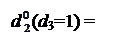
 1, якщо NA2П = NВ;
1, якщо NA2П = NВ;
0, якщо NA2П ≠ NВ.
Звідси дістанемо:
d  ( d3 = 1) =
( d3 = 1) = 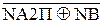 (3.160)
(3.160)
Узагальнюючи (3.154) – (3.155) і (3.160), маємо:
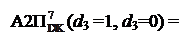
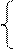 (А3П
(А3П  + ВР2
+ ВР2  )m128, якщо NA3П ≠ NВ;
)m128, якщо NA3П ≠ NВ;
(А3П  +
+ 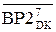 +1)m128, якщо NA3П=NВ; (3.161)
+1)m128, якщо NA3П=NВ; (3.161)
d  (d3 = 1, d3=0) =
(d3 = 1, d3=0) = 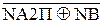 . (3.162)
. (3.162)
Таким чином, загальна форма визначення залишку діленого і обчислен-ня цифр частки при діленні (-МА)DK на (+МВ)DK тотожня відповідним залеж-ностям при діленні (+МА)DK на (-МВ)DK, але при нульовій остачі ділення чисел (С=0) алгоритм ділення чисел (-МА)DK на (+МВ)DK має певні особли-вості.
У загальному випадку, при діленні (-МА)DK на (+МВ)DK підсумкова остача дорівнює нулю (С = 0), якщо ділене, дільник і частка пов’язані співвідношенням:
(-МА) = (-МD)* МВ = - (МВ×22× d3 + МВ×21× d2 + МВ× d1),
де МD = d3d2d1 = (001 ÷ 111) – можливі сполучення цифр модуля частки.
У випадку, коли модуль частки МD(3/1) = d3d2d1 = 100, очевидно, част-кові залишки діленого набувають значень:
А3 = - (МА - МВ×22) = МВ×21× d2+ МВ× d1 = МВ×21× 0 + МВ×0 = 0,
А2 = - (МА - МВ×22 - МВ×21) = - (0 - МВ×21) = (+МВ×21);
А1 = - (МА - МВ×22× d3 - МВ×21× d2- МВ) =
= - (МА – МВ×22 - МВ×21× 0 – МВ) = - (0 – МВ) = (+МВ).
Звідси випливає, що за визначеним загальним комп’ютерним алгорит-мом ділення (-МА)DK = (-4MВ)DK на (+МВ)DK дістанемо:


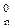 частки визначається за формулою:
частки визначається за формулою: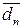 .
.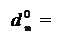
 NА4П ÅNB, якщо А4П = 0;
NА4П ÅNB, якщо А4П = 0;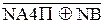 , якщо А4П ≠ 0. (3.143)
, якщо А4П ≠ 0. (3.143)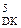

 X X X X X
X X X X X

 X X X X 1
X X X X 1
 ND
ND 
 X X X 1 1
X X X 1 1
 1 1 0 0 1 1 0
1 1 0 0 1 1 0


 NA NB
NA NB

 ND
ND
 0 1 0 1 0 0 0
0 1 0 1 0 0 0


 NB=0
NB=0

 о
о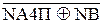 =1
=1
 0 1 0 1 0 0 0
0 1 0 1 0 0 0


 NВ ≠ NА
= A7DK
NВ ≠ NА
= A7DK
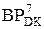 = А4ПDК (А4П≠0)
= А4ПDК (А4П≠0)
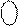
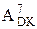 = 1 100 110
= 1 100 110

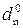 = 1 при
= 1 при
 ND
ND 
 0 1 0 1 0 0 0
0 1 0 1 0 0 0

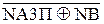 = 0
= 0 = А4П
= А4П  DР
DР  А
А 
 ВP
ВP  ND
ND


 ND
1 0 1 1 0 0 0
ND
1 0 1 1 0 0 0
 0 1 0 1 0 0 0
0 1 0 1 0 0 0


 = A
= A 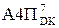 (А4ПDK = 0)
(А4ПDK = 0)
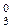 обчислюється зі зсувом дільника вправо, тобто за алгоритмом «б».
обчислюється зі зсувом дільника вправо, тобто за алгоритмом «б».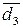 = 0, якщо А3 > 0, інакше d
= 0, якщо А3 > 0, інакше d 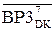 + 1)m128, (3.148)
+ 1)m128, (3.148)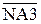 (за А3≠0).
(за А3≠0).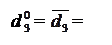
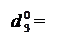
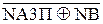 (3.149)
(3.149)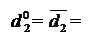
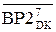 + 1)m128 (3.154)
+ 1)m128 (3.154)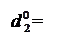
 ( d3 = 0) =
( d3 = 0) = 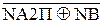 (3.155)
(3.155)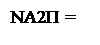
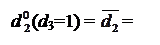
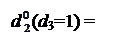
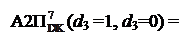
 (А3П
(А3П