0, якщо NА3П ≠ NВ.
Звідси дістанемо:
d  =
= 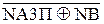 (3.122)
(3.122)
де NА3П – знак залишку А3П за операцією (3.119).
Алгоритм визначення наступної позиції d 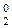 частки залежить від стану позиції d3 частки у попередньому циклі.
частки залежить від стану позиції d3 частки у попередньому циклі.
Спочатку побудуємо алгоритм визначення позиції d  частки за d3=0 (d
частки за d3=0 (d  =
= 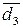 =1).
=1).
За d3=0 початковий стан числових змінних після обчислення позиції d3, очевидно, визначається співвідношеннями:
А3(d3=0) = (-МА3)<0; (3.123)
ВР2 = (-МВ2), (3.124)
де (-МА3) = (МА – МВ3) – залишок діленого після логічного обчислення позиції d3 частки;
МВР2 = (МВР3/2) – стан модуля дільника після логічного зсуву на один біт вправо стану модуля дільника у попередньому циклі ділення чисел.
За цих умов маємо:
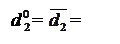
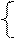 1, якщо А2 < 0;
1, якщо А2 < 0;
0, якщо А2 ≥ 0, (3.125)
де А2 = (МА – МВР2) - (3.126)
- залишок діленого для визначення позиції d2 частки.
Із урахуванням (3.123) – (3.124) перетворимо (3.126), записавши його у вигляді:
А2 = МА – МВР2 = - МА3 +МВР3 – МВР2 =-МА3 + МВР3 – МВР3/2 =
= - МА3 + МВР3/2 = -МА3 + МВР2 = (-МА3) - (-МВР2) = (А3 – ВР2).
Таким чином, доповняльний код залишку А2 можна подати у вигляді:
А2  (d3=0) = (128 + А3 – ВР2)m128 = (А3
(d3=0) = (128 + А3 – ВР2)m128 = (А3  +
+ 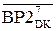 + 1), (3.127)
+ 1), (3.127)
де А3  = (- МА3)
= (- МА3)  ; ВР2
; ВР2  = (+МВР2)
= (+МВР2)  .
.
Згідно з властивостями доповняльного коду маємо:
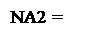
 0, якщо А2 ≥ 0;
0, якщо А2 ≥ 0;
1, якщо А2 < 0.
Тоді нерівності (3.125) набувають вигляду:
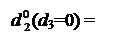
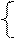 1, якщо NА2 = 1;
1, якщо NА2 = 1;
0, якщо NА2 = 0.
При діленні (+МА)DK на (-МВ)DK знак дільника NВ=1, тому ці залежнос-ті можна пов’язати зі знаком NВ співвідношеннями:
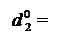
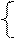 1, якщо NА2 = NВ;
1, якщо NА2 = NВ;
0, якщо NА2 ≠ NВ.
Звідси дістанемо:
d  =
= 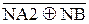 . (3.128)
. (3.128)
Якщо найстарша позиція частки d3 = 1, то початковий стан сукупності числових змінних після обчислення позиції d  частки визначаються рівнян-нями:
частки визначаються рівнян-нями:
А3(d3 = 1) = (+МА3); (3.129)
ВР2 = (- МВР2), (3.130)
де МА3 = (МА – МВР3) - (3.131)
– модуль часткового залишку діленого у попередньому циклі;
МВР2 = (МВР3/2) – стан модуля дільника після логічного зсуву на один біт вправо стану модуля дільника у попередньому циклі ділення чисел.
У загальному випадку розряд частки d  визначається нерівностями виду:
визначається нерівностями виду:
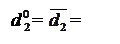
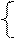 1, якщо А2 < 0;
1, якщо А2 < 0;
0, якщо А2 ≥ 0,
де А2 = (МА3 – МВР2). (3.132)
Із урахуванням (3.129) – (3.130) перетворимо (3.132) наступним чином: А2 = МА3 – МВР2 = (+МА3) + (-МВР2) =(А3 + ВР2).
Із цього випливає, що доповняльний код часткового залишку А2 визначається співвідношенням:
А2  (d3=1) = (128 + (А3 + ВР2))m128 = (А3
(d3=1) = (128 + (А3 + ВР2))m128 = (А3  + ВР2
+ ВР2  ) m128, (3.133)
) m128, (3.133)
де А3  = (+ МА3)
= (+ МА3)  ; ВР2
; ВР2  = (-МВР2)
= (-МВР2)  .
.
Згідно з властивостями доповняльного коду маємо:
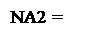
 0, якщо А2 ≥ 0;
0, якщо А2 ≥ 0;
1, якщо А2 < 0.
Тоді нерівності (3.132) можна подати у вигляді:
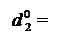
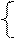 1, якщо NА2 = 1;
1, якщо NА2 = 1;
0, якщо NА2 = 0.
За операцією ділення (+МА)DК на (-МВ)DК знак дільника NВ=1, тому позиція d  частки може бути пов’язана зі знаком дільника співвідношеннями:
частки може бути пов’язана зі знаком дільника співвідношеннями:
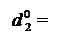
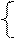 1, якщо NА2 = NВ;
1, якщо NА2 = NВ;
0, якщо NА2 ≠ NВ.
Звідси дістанемо:
d  ( d3=1)=
( d3=1)= 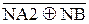 . (3.134)
. (3.134)
Узагальнюючи (3.127), (3.128), (3.133) і (3.134), маємо:
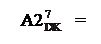
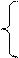 (А3
(А3  +
+ 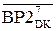 +1)m128, якщо NA3 = NB;
+1)m128, якщо NA3 = NB;
(А3  + BP2
+ BP2  )m128, якщо NA3 ≠ NB;
)m128, якщо NA3 ≠ NB;
d 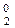 =
= 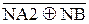 . (3.135)
. (3.135)
Із цих залежностей випливає, що форма визначення часткових залишків діленого і цифр частки повністю тотожня відповідним залежностям при діленні (+МА)DК на (+МВ)DК. Відмінність ділення (+МА) DК на (-МВ)DК полягає тільки у тому, що у цьому випадку знак частки ND = 1 і згідно з (3.64) після закінчення операції ділення двійковий рядок оберненого коду частки (d 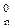 d
d  d
d  d
d  ) підлягає коректуванню шляхом додавання одиниці до молодшого розряду частки d
) підлягає коректуванню шляхом додавання одиниці до молодшого розряду частки d  .
.
Розглянемо тепер задачу визначення остачі С від ділення (+МА)DК на (-МВ)DК.
Очевидно, що аргументи операції ділення і результат у даному випадку пов’язані співвідношенням:
(+МА) = (-МВ)* (-МD) + С.
У розгорненій формі маємо:
С = МА – МВ(22×d3 + 21×d2 + 20×d1).
Звідси дістанемо:
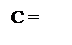
 МА – МВ(d3×22 + d2×21+ 20), якщо d1=1;
МА – МВ(d3×22 + d2×21+ 20), якщо d1=1;
МА – МВ(d3×22 + d2×2), якщо d1= 0.
Відомо, що в останньому циклі ділення частковий залишок діленого А1 обчислюється за формулою:
А1 = МА – МВ(d3×22 + d2×21+ 1×20) =
= МА – (МВ×22)d3 + (МВ×21)d2 – МВ.
Таким чином, останній залишок діленого у загальному випадку взаємо- пов'язаний з остачею С співвідношеннями:
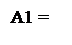
 С, якщо d1=1, тобто А1≥ 0;
С, якщо d1=1, тобто А1≥ 0;
С - МВ, якщо d1=0, тобто А1< 0.
Звідси випливає:
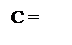
 А1, якщо А1≥ 0, тобто NA1 = NA;
А1, якщо А1≥ 0, тобто NA1 = NA;
А1-(-МВ), якщо А1< 0, тобто NA1 ≠ NA,
де NA = (NDÅNB) – первинний знак діленого.
Звідси дістанемо:
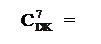
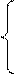 А1
А1  , якщо NA1 = (NB Å ND) і (NA1≠ NВ);
, якщо NA1 = (NB Å ND) і (NA1≠ NВ);
(А1  + (
+ ( 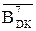 +1))m128, якщо NA1 ≠ (NB Å ND) і (3.136)
+1))m128, якщо NA1 ≠ (NB Å ND) і (3.136)
(NA1 = NB),
де ( 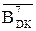 +1) = (+МВ)
+1) = (+МВ)  ; В
; В  = (- МВ)
= (- МВ)  .
.
Приклади ділення (+МА)DК на (-МВ)DК на основі побудованих правил визначення доповняльного коду результату за алгоритмами «б» і «а» подано на рис. 3.26 – 3.27.
Побудуємо тепер алгоритм ділення (-МА)DК на (+МВ)DК .
За цих аргументів первинні змінні діленого і дільника при діленні чисел набувають вигляду:
А = (-МА); (3.137)
ВР = (+ МВР), (3.138)
де МА, МВР – відповідно модуль подвійного формату діленого і модуль розширеного подвійного формату дільника;
Відомо, що розшир частки dn=1 при діленні МА на МВ виникає у тому випадку, коли МА ≥ МВР.
Отже, маємо:
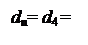
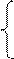 1, якщо А4 = 0;
1, якщо А4 = 0;
1, якщо А4 > 0 (А4 ≠ 0) ;
0, якщо А4 < 0 (А4 ≠ 0), (3.139)
де А4 = (МА – МВР) - (3.140)
– частковий залишок модуля діленого для визначення позиції 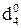 (
( 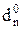 ) частки.
) частки.
Для визначення залишку А4 у доповняльному коді перетворимо (3.140) наступним чином:
А4П = (-А4) = (-МА + (+МВР)),
де А4П – залишок діленого, протилежний залишку А4.
Звідси дістанемо:
(А4П)  = (128 + (-МА + (+ МВР))m128=
= (128 + (-МА + (+ МВР))m128=
= (128 + А + ВР) m128 = (A  + BP
+ BP  ) m128 (3.141)
) m128 (3.141)
де A  = (- МА)
= (- МА)  ; ВР
; ВР  =(+МВР)
=(+МВР)  .
.
Очевидно, що знак залишку А4П (NА4П) пов'язаний зі знаком А4(NA4) співвідношеннями:
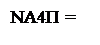
 NА4, якщо А4П = 0 (NА4П = 0);
NА4, якщо А4П = 0 (NА4П = 0);
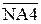 , якщо А4П < 0. (3.142)
, якщо А4П < 0. (3.142)
Із урахуванням (3.142) залежності (3.139) набувають вигляду:
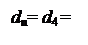
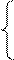 1, якщо А4П = 0 (NА4П = 0);
1, якщо А4П = 0 (NА4П = 0);
1, якщо NА4П = 1 (NА4П = 1, NА4 = 0, А4П≠0);
0, якщо NА4П = 0 (NА4П = 0, NА4=1, А4П≠0).
При діленні (-МА)DК на (+МВ)DК знак дільника NВ = 0, тому розшир dn може бути пов’язаний зі знаком дільника нерівностями виду:
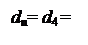

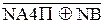 , якщо А4П = 0;
, якщо А4П = 0;
NА4П ÅNB, якщо А4П ≠ 0.
Рисунок 3.26 – Приклад ділення (+МА) DК на (-МВ)DК за алгоритмом «б»


 =
= 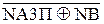 (3.122)
(3.122)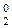 частки залежить від стану позиції d3 частки у попередньому циклі.
частки залежить від стану позиції d3 частки у попередньому циклі. частки за d3=0 (d
частки за d3=0 (d 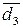 =1).
=1).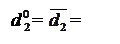
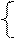 1, якщо А2 < 0;
1, якщо А2 < 0; (d3=0) = (128 + А3 – ВР2)m128 = (А3
(d3=0) = (128 + А3 – ВР2)m128 = (А3 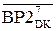 + 1), (3.127)
+ 1), (3.127)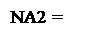
 0, якщо А2 ≥ 0;
0, якщо А2 ≥ 0;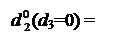
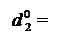
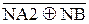 . (3.128)
. (3.128)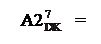
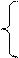 (А3
(А3 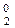 =
= 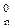 d
d  ) підлягає коректуванню шляхом додавання одиниці до молодшого розряду частки d
) підлягає коректуванню шляхом додавання одиниці до молодшого розряду частки d 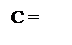
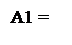
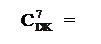
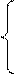 А1
А1 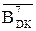 +1))m128, якщо NA1 ≠ (NB Å ND) і (3.136)
+1))m128, якщо NA1 ≠ (NB Å ND) і (3.136)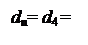
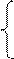 1, якщо А4 = 0;
1, якщо А4 = 0;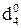 (
( 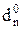 ) частки.
) частки.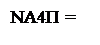
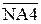 , якщо А4П < 0. (3.142)
, якщо А4П < 0. (3.142)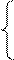 1, якщо А4П = 0 (NА4П = 0);
1, якщо А4П = 0 (NА4П = 0);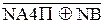 , якщо А4П = 0;
, якщо А4П = 0;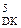
 X X X X X
ND = NA ÅNB = 1
X X X X X
ND = NA ÅNB = 1



 ND
ND 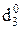 = NA3 Å NB = 0
= NA3 Å NB = 0
 ND
ND 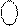
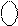 X X 1 1 0
X X 1 1 0
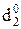 = NA2 Å NB = 0
= NA2 Å NB = 0

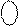
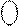
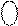

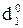 = NA1 Å NB = 1
= NA1 Å NB = 1
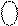
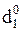
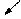


 ND
ND
 + 1
+ 1

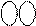
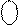
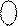
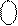

 ND
ND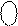 0 0 0 1 1 0 1
0 0 0 1 1 0 1
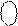


 1 1 1 1 1 0 1
1 1 1 1 1 0 1

 0 0 0 0 1 0 1
0 0 0 0 1 0 1


 NA2
NA2
 0 0 0 0 0 0 1
0 0 0 0 0 0 1

 =
=  NA ≠NB
=
NA ≠NB
= 
 BP
BP


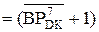 NA4=NB
=
NA4=NB
= 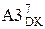
 BP
1 1 1 1 1 0 0
BP
1 1 1 1 1 0 0

 =
= 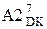


 =
= 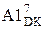 NA1 = NB
NA1 = NB
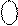 DР
DР 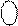 А
А  4 3 2 1
4 3 2 1



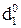 = NA1ÅNB = 1
= NA1ÅNB = 1



 1 1 0 1 0
1 1 0 1 0 ND
ND
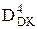

 0 0 0 1 0 1 0
0 0 0 1 0 1 0
 1 1 1 0
1 1 1 0


 3
3
 0 0 0 0 0 0 1
0 0 0 0 0 0 1
 =
= 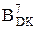 NA ≠NB
=
NA ≠NB
= 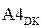
 =
= 

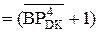 NA4=NB
=
NA4=NB
= 
 =
=  =
= 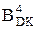 NA3≠NB
NA3≠NB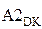


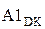
 NA1 = NB
NA1 = NB