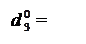Приклад ділення (+МА)DK на (+МВ) DK за алгоритмом «а» при застосу-ванні скороченого формату дільника подано на рис.3.23.
Рисунок 3.23 – Приклад ділення (+МА)DК на (+МВ)DК за алгоритмом «а»
при застосуванні скороченого формату дільника
Побудуємо тепер алгоритм визначення цифр частки від ділення (+МА)DК на (-МВ)DК .
За цих умов первинний стан діленого і дільника за загальним алгоритмом ділення визначаються числовими змінними:
А = (+ МА); (3.106)
ВР = (- МВ), (3.107)
де А, ВР – відповідно подвійний формат діленого і розширений подвійний формат знормованого дільника;
У даному випадку NA=0 і NB=1, тому ND = NAÅNB = 1. Тоді згідно з (3.66) обчислення ознаки переповнення розширеного формату частки повинно визначатися за співвідношенням:
d 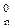 =
= 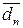 =
= 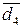 .
.
Відомо, що в прямому виді d4 = 1 у тому випадку, коли МА≥МВР, тому розшир dn(d4) потрібно визначати нерівностями виду:
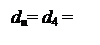
 1, якщо А4 ≥ 0;
1, якщо А4 ≥ 0;
0, якщо А4 < 0. (3.108)
де А4 = (МА – МВР) - (3.109)
– залишок модуля діленого після віднімання подвійного розширеного формату дільника МВР.
Для визначення залишку А4 у доповняльному коді перетворимо (3.109) наступним чином:
А4 = (+МА) + (- МВР).
Звідси згідно з (3.105) і (3.106) дістанемо:
А4 = А + ВР.
Із цього випливає, що залишок А4 у доповняльному коді А4  потрібно обчислювати за формулою:
потрібно обчислювати за формулою:
А4  = (128+ (А+ВР))m128 = (А
= (128+ (А+ВР))m128 = (А  + BP
+ BP  ) m128, (3.110)
) m128, (3.110)
де А  = (+МА)
= (+МА)  ; BP
; BP  = (-МВР)
= (-МВР)  .
.
Згідно властивостей доповняльного коду маємо:
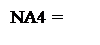
 0, якщо А4 ≥ 0;
0, якщо А4 ≥ 0;
1, якщо А4 < 0. (3.111)
де NA4 – знак залишку А4  .
.
Через те, що при діленні (+МА)DК на (-МВ)DК знак дільника NB=1, розшир dn може бути пов’язаний зі знаком дільника NB рівнянням:
dn = (NA4 Å NB), (3.112)
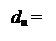 тобто
тобто  0, якщо NA4 = NВ;
0, якщо NA4 = NВ;
1, якщо NA4 ≠ NВ.
Отже , згідно з (3.107) розшир d 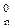 від’ємної частки при діленні (+МА)DК на (-МВ)DК повинен формуватися за рівнянням:
від’ємної частки при діленні (+МА)DК на (-МВ)DК повинен формуватися за рівнянням:
d 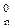 =
= 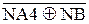 . (3.113)
. (3.113)
Приклади визначення позиції d 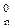 від’ємної частки при діленні (+МА)DК на (-МВ)DК подано на рис.3.24 - 3.25.
від’ємної частки при діленні (+МА)DК на (-МВ)DК подано на рис.3.24 - 3.25.
Припустімо, що обчислення найстаршої цифри частки d  виконується зі зсувом дільника вправо, тобто за алгоритмом «б».
виконується зі зсувом дільника вправо, тобто за алгоритмом «б».
Початковий стан числових змінних, за якими визначається позиція d  частки має вигляд:
частки має вигляд:
A4 = (- MA4); (3.114)
BP3 = (-МВР3), (3.115)
Рисунок 3.24 – Приклад визначення позиції 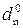 = 1
= 1
при діленні (+МА)DK на (-МВ)DK
Рисунок 3.25 – Приклад визначення позиції 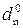 = 0 частки
= 0 частки
при діленні (+МА)DK на (-МВ)DK
де МА4 = |МА – МВР| – модуль залишку діленого за dn = 0;
МВР3 = (МВР/2) – стан модуля дільника після логічного зсуву на один біт вправо розширеного подвійного модуля дільника МВР.
Згідно з (3.66) при діленні (+МА)DК на (-МВ)DК справедливі співвідно-шення:
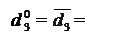
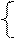 1, якщо А3 ≥ 0;
1, якщо А3 ≥ 0;
0, якщо А3 < 0, (3.116)
де А3 = (МА – МВР3). (3.117)
Із урахуванням (3.114) – (3.115) перетворимо (3.117), записуючи його у вигляді:
(-А3) = А3П = (-МА) – (-МВР3) = (А4 – ВР3), (3.118)
де А3П – залишок діленого, протилежний залишку А3.
Із цього випливає, що доповняльний код числової змінної АЗП повинен визначитися співвідношенням:
АЗП  = (128+(А4 – ВР3))m128 = ((128+А4)m128 – (128+ВР3)m128)m128=
= (128+(А4 – ВР3))m128 = ((128+А4)m128 – (128+ВР3)m128)m128=
= (А4  + 128 – ВР3
+ 128 – ВР3  )m128=(А4
)m128=(А4  + (127– ВР3
+ (127– ВР3  ) + 1)m128 =
) + 1)m128 =
= (А4  +
+ 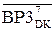 + 1) m128 . (3.119)
+ 1) m128 . (3.119)
Звідси дістанемо:
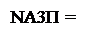
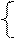 0, якщо А3 < 0;
0, якщо А3 < 0;
1, якщо А3 ≥ 0, (3.120)
де NA3П = 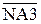 - знак числової змінної АЗП = (-А3).
- знак числової змінної АЗП = (-А3).
Із урахуванням залежностей (3.120) нерівності (3.116) набувають вигляду:
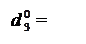
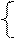 1, якщо NА3П = 1;
1, якщо NА3П = 1;
0, якщо NА3П = 0, (3.121)
Через те, що при діленні (+МА) на (-МВ) знак дільника NВ = 1, нерівності (3.121) можна записати у вигляді:
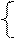 1, якщо NА3П = NВ;
1, якщо NА3П = NВ;



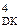
 X X X X X
X X X X X



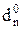 X X X 0 0
X X X 0 0


 ND
ND 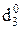
 X X 0 0 1
X X 0 0 1


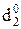
 ND
ND 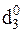
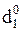
 0 0 1 1 0
0 0 1 1 0
 0 0 0 1 1 0 1
0 0 0 1 1 0 1

 NA
NA
 1 1 1 0
1 1 1 0

 1 1 1 1 1 0 1
1 1 1 1 1 0 1
 0 0 1 0
0 0 1 0
 0 0 0 1 0 1 0
0 0 0 1 0 1 0
 0 0 1 0 1 0 0
0 0 1 0 1 0 0

 NA2
NA2
 1 1 1 0
1 1 1 0
 0 0 1 0
0 0 1 0
 3 p
3 p 0 0 0 0 0 0 1
0 0 0 0 0 0 1
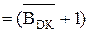 NA =NB
=
NA =NB
= 

 =
= 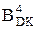 NA4 ≠ NB
=
NA4 ≠ NB
= 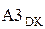

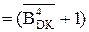 NA3 = NB
NA3 = NB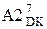


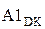

 =
= 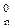 =
= 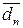 =
= 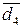 .
.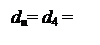
 1, якщо А4 ≥ 0;
1, якщо А4 ≥ 0;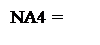
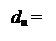 тобто
тобто 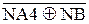 . (3.113)
. (3.113) виконується зі зсувом дільника вправо, тобто за алгоритмом «б».
виконується зі зсувом дільника вправо, тобто за алгоритмом «б». X X X X X
X X X X X

 X X X X 1
X X X X 1
 ND
ND 
 X X X 1 1
X X X 1 1
 0 0 1 1 0 1 0
0 0 1 1 0 1 0

 NA
NA
 ND
ND 
 1 0 1 1 0 0 0
1 0 1 1 0 0 0


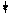 NA4 NB=1
NA4 NB=1




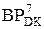 = А4
= А4 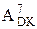 = 0 011 010
= 0 011 010
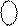
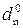 = 1
= 1
 NA4 NB=1
NA4 NB=1

 = (А4)DК
= (А4)DК
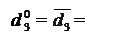
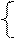 1, якщо А3 ≥ 0;
1, якщо А3 ≥ 0;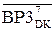 + 1) m128 . (3.119)
+ 1) m128 . (3.119)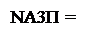
 - знак числової змінної АЗП = (-А3).
- знак числової змінної АЗП = (-А3).