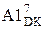частки і наявності ознаки ПП частки при діленні (+МА)DK на (+МВ)DK
А4 = (- МА4); ( 3.78 )
ВР = (+ МВ3), ( 3.79 )
де МА4 = |МВР – МА| – модуль часткового залишку діленого у поперед-ньому циклі за ПП = 0;
МВР3 = (МВР/2) – стан модуля дільника після логічного зсуву на один біт вправо стану подвійного розширеного модуля дільника МВР;
Згідно з (3.65) при діленні (+МА)DK на (+МВ)DK для визначення цифри d  частки справедливі співвідношення:
частки справедливі співвідношення:
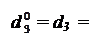
 1, якщо А3 ≥ 0;
1, якщо А3 ≥ 0;
0, якщо А3 < 0, ( 3.80 )
де А3 = (МА – МВР/2) = (МА – МВР3); МВР3 = МВР/2.
Із урахуванням (3.78) і (3.79) перетворимо вираз А3, записуючи його у вигляді:
А3 = МА – МВР3 = (-МА4 + МВР – МВР3) =
= ((-МА4) + МВР – МВР/2)) = (-МА4) + (МВР/2) =
= (-МА4) + (МВР3) = А4 + ВР3. ( 3.81 )
Із цих міркувань випливає, що доповняльний код залишку А3 потрібно обчислювати за формулою:
А3  = (128 + А4 + ВР3) m128 = (А4
= (128 + А4 + ВР3) m128 = (А4  + ВР3
+ ВР3  ) m128 . ( 3.82 )
) m128 . ( 3.82 )
Згідно з властивостями доповняльного коду маємо:
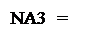
 1, якщо А3 < 0;
1, якщо А3 < 0;
0, якщо А3 ≥ 0, ( 3.83 )
де NA3 – знак доповняльного коду числової змінної А3.
За умови (3.83) нерівності (3.80) набувають вигляду:
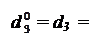
 1, якщо NA3 = 0;
1, якщо NA3 = 0;
0, якщо NA3 = 1. ( 3.84 )
Через те, що при діленні (+МА)DK на (+МВ)DK знак дільника NВ = 0, цифру d  згідно з (3.84) можна пов’язати зі знаком NВ співвідношенням:
згідно з (3.84) можна пов’язати зі знаком NВ співвідношенням:
d  = d3 =
= d3 = 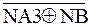 ( 3.85 )
( 3.85 )
При визначені наступної цифри частки d  початковий стан змінних залежить від значення цифри d3 частки, визначеної у попередньому циклі.
початковий стан змінних залежить від значення цифри d3 частки, визначеної у попередньому циклі.
Якщо d3 = 0, то початковий стан числових змінних при визначенні позиції d  частки набуває вигляду:
частки набуває вигляду:
А3 (d3 = 0) = (-МА3); ( 3.86 )
ВР2 = (+ МВР2), ( 3.87 )
де МА3 = |МА – МВР3| - ( 3.88 )
- модуль залишку діленого А3 за d3 = 0 (МА < МВР3);
МВР2 = МВР3/2 - ( 3.89 )
- стан модуля дільника після логічного зсуву на один біт вправо модуля МВ3 (стану дільника у попередньому циклі).
Таким чином, згідно з (3.86) і (3.87) залишок діленого для визначення позиції d 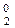 частки потрібно обчислювати за співвідношенням:
частки потрібно обчислювати за співвідношенням:
А2 = МА – МВР2 = (- МА3 + МВР3) – МВР2 =
= (- МА3) + МВР2 = А3 + ВР2.
Звідси дістанемо:
А2  (d3 = 0) = (А3
(d3 = 0) = (А3  + ВР2
+ ВР2  ) m128 ,
) m128 ,
де А3  = (-МА3)
= (-МА3)  ; ВР2
; ВР2  = (+МВР2)
= (+МВР2)  .
.
Згідно з властивостями доповняльного коду маємо:
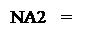
 0, якщо A2 ≥ 0;
0, якщо A2 ≥ 0;
1, якщо A2 < 0, ( 3.90 )
де NA2 – знак доповняльного коду залишку А2.
Тоді нерівності (3.90) можна подати у вигляді
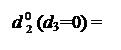
 1, якщо NA2 = 0;
1, якщо NA2 = 0;
0, якщо NA2 = 1.
При діленні (+МА)DK на (+MB)DK знак дільника NB=0, тому обчислення позиції d 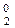 частки можна пов’язати зі знаком дільника NB таким чином:
частки можна пов’язати зі знаком дільника NB таким чином:
d 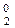 (d3 = 0) =
(d3 = 0) = 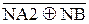 ( 3.91 )
( 3.91 )
Якщо цифра частки d3 = 1, то початковий стан сукупності числових змінних при визначенні позиції d 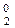 частки набуває вигляду:
частки набуває вигляду:
А3(d3 = 1) = (+МА3);
ВР2 = (+МВР2),
де МА3 = (МА – МВР3) – ( 3.92 )
- модуль залишку А3 за d3 = 1 (МА > МВР3);
МВР2 = МВР3/2 - ( 3.93 )
– стан модуля дільника після логічного зсуву на один біт вправо МВ3 (стану дільника у попередньому циклі).
Згідно з (3.65), значення цифри d 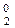 частки за ND=0 потрібно обчислю-вати за нерівностями виду:
частки за ND=0 потрібно обчислю-вати за нерівностями виду:
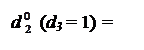
 1, якщо A2 ≥ 0;
1, якщо A2 ≥ 0;
0, якщо A2 < 1,
де А2 = (МА – МВР3 – МВР2). ( 3.94 )
Із урахуванням (3.92) і (3.93) перетворимо (3.94) наступним чином:
А2 = МА3 – МВР2 = (+МА3) + (-МВР2) = А3+ (-ВР2) = (А3 – ВР2).
Із цих міркувань випливає, що доповняльний код залишку А2 потрібно визначати за співвідношенням:
А2  (d3 = 1) = (128 + А3 – ВР2)m128 =
(d3 = 1) = (128 + А3 – ВР2)m128 =
= (А3  +
+ 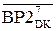 + 1) m128. ( 3.95 )
+ 1) m128. ( 3.95 )
Згідно властивостей доповняльного коду маємо:
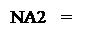
 0, якщо A2 ≥ 0;
0, якщо A2 ≥ 0;
1, якщо A2 < 0,
де NA2 – знак числової змінної А2  .
.
Тоді нерівності (3.94) можна подати у вигляді:
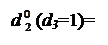
 0, якщо NA2 = 1;
0, якщо NA2 = 1;
1, якщо NA2 = 0.
При діленні (+МА) на (+МВ) знак дільника NB=0, тому визначення позиції d 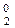 частки можна пов’язати зі знаком NB співвідношенням:
частки можна пов’язати зі знаком NB співвідношенням:
d 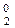 (d3 = 1) =
(d3 = 1) = 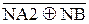 . ( 3.96 )
. ( 3.96 )
Узагальнюючи (3.90), (3.95), (3.91) і (3.96), отримаємо наступну сукупність рекурентних формул для визначення цифри d 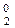 частки при діленні (+МА)DK на (+MB)DK :
частки при діленні (+МА)DK на (+MB)DK :
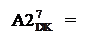
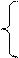 (А3
(А3  + (BP2)
+ (BP2)  )m128 при NA3 ≠ NB;
)m128 при NA3 ≠ NB;
(А3  +
+ 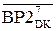 +1)m128 при NA3 = NB; ( 3.97 )
+1)m128 при NA3 = NB; ( 3.97 )
d 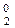 =
= 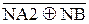 , ( 3.98 )
, ( 3.98 )
де А3  - залишок діленого для визначення позиції d
- залишок діленого для визначення позиції d  частки у попередньому циклі;
частки у попередньому циклі;
(BP2)  =(BP3/2)
=(BP3/2)  ; ВР3=(+МВР/2) – стан додатного дільника у по-передньому циклі операції ділення при визначенні позиції d
; ВР3=(+МВР/2) – стан додатного дільника у по-передньому циклі операції ділення при визначенні позиції d  частки;
частки;
МВР – початковий стан подвійного розширеного формату модуля дільника.
Співвідношення (3.97) і (3.98) для визначення залишку А2  і обчис-лення цифри d
і обчис-лення цифри d 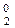 частки згідно з (3.74), (3.77), (3.82) і (3.85) функціонально збігається з відповідними залежностями для визначення (А4)DK, (А3)DK, d
частки згідно з (3.74), (3.77), (3.82) і (3.85) функціонально збігається з відповідними залежностями для визначення (А4)DK, (А3)DK, d 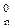 і d
і d  , тобто являють собою узагальнену форму алгоритму ділення (+МА)DK на (+МВ)DK. Згідно з цим логічним законом дістанемо:
, тобто являють собою узагальнену форму алгоритму ділення (+МА)DK на (+МВ)DK. Згідно з цим логічним законом дістанемо:
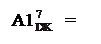
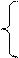 [А2
[А2  + (BP1)
+ (BP1)  ]m128 при NA2 ≠ NB;
]m128 при NA2 ≠ NB;
(А2  +
+ 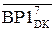 +1)m128 при NA2 = NB; ( 3.99 ) d
+1)m128 при NA2 = NB; ( 3.99 ) d 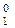 =
= 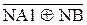 , (3.100)
, (3.100)
де (BP1)  = (BP2)
= (BP2)  /2.
/2.
Розглянемо тепер задачу визначення остачі від ділення (+МА)DK на (+МВ)DK.
Згідно з правилами арифметики у загальному випадку аргументи і результат операції ділення пов’язані співвідношенням:
МА = МВ*MD + C,
де МА, МВ, MD, С – відповідно цілочислові модулі діленого, дільника, частки і остачі.
Таким чином, остача операції ділення С повинна визначатися за формулою:
С = МА – МВ* MD.
У розгорнутій формі маємо:
С = МА – МВ*(d3×22 + d 2×21 + d1×20),
Звідси дістанемо:

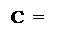 МА – МВ*(d3×22 + d 2×21 + 1), якщо d1= 1;
МА – МВ*(d3×22 + d 2×21 + 1), якщо d1= 1;
МА – МВ*(d3×22 + d 2×21), якщо d1= 0.
Відомо, що в останньому циклі ділення частковий залишок діленого А1 обчислюється за формулою:
А1 = МА – (МВ×22)×d3 – (МВ×21)× d2 – МВ.
Таким чином, частковий залишок А1 діленого у загальному випадку взаємопов’язаний з остачею С співвідношенням:
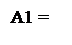
 С, якщо d1= 1, тобто за А1≥ 0;
С, якщо d1= 1, тобто за А1≥ 0;
С-МВ, якщо d1= 0, тобто за А1< 0.
Звідси випливає:
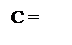
 А1, якщо А1≥ 0;
А1, якщо А1≥ 0;
А1 + МВ, якщо А1< 0.
Отже, при діленні (+МА)DK на (+МВ) DK, тобто за NB = 0 і ND = 0, доповняльний код остачі операції ділення повинен визначатися за нерівностями виду:
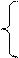
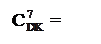 А1
А1  , якщо NA1 = (ND Å NB);
, якщо NA1 = (ND Å NB);
(А1  +B
+B  )m128, якщо NA1≠(NDÅNB), (3.101)
)m128, якщо NA1≠(NDÅNB), (3.101)
де (ND Å NB) = NA – первинний знак діленого; B  = (+МВ)
= (+МВ)  .
.
Приклади ділення (+МА)DK на (+МВ) DK згідно з логічними виразами (3.97) – (3.101) за алгоритмом «б» подано на рис. 3.22.
Якщо цифри частки визначаються за алгоритмом «а», тобто шляхом зсуву вліво часткових залишків діленого при нерухомому дільнику, то залежності (3.97) – (3.100) набувають вигляду:
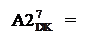
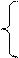 (2×А3
(2×А3  + BР
+ BР  )m128 при NA3 ≠ NB;
)m128 при NA3 ≠ NB;
(2×А3  +
+ 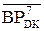 +1)m128 при NA3 = NB; (3.102) d
+1)m128 при NA3 = NB; (3.102) d 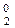 =
= 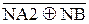 ; (3.103)
; (3.103)
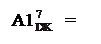
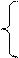 (2×А2
(2×А2  + BР
+ BР  )m128 при NA2 ≠ NB;
)m128 при NA2 ≠ NB;
(2×А2  +
+ 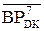 +1)m128 при NA2 = NB; (3.104) d
+1)m128 при NA2 = NB; (3.104) d 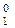 =
= 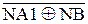 , (3.105)
, (3.105)
де ВР = (+МВ000) – розширений подвійний формат нерухомого дільника;
МВ = b3b2b1 – рядок цифр первинного модуля дільника при діленні [+МА(6/1)]DK на [+МВ(3/1)]DK .
Зазначимо, що доповняльний код нерухомого розширеного коду дільника ВР можна представити в такому скороченому вигляді:
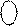
 BР
BР  = (+b3b2b1000)
= (+b3b2b1000)  = 0 b3b2b1000 = [ 0 b3b2b1]× 23;
= 0 b3b2b1000 = [ 0 b3b2b1]× 23;
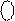
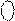 (
( 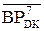 +1) =
+1) = 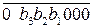 + 1 = 1
+ 1 = 1 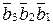 111 + 1 =
111 + 1 =
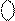
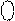 = 1
= 1 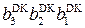 000 = [ 1
000 = [ 1 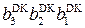 ]×23 ,
]×23 ,
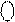
 де [ 0 b3b2b1], [ 1
де [ 0 b3b2b1], [ 1 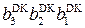 ] – відповідно доповняльний код додатного і від’ємного дільника за чотирирозрядним форматом.
] – відповідно доповняльний код додатного і від’ємного дільника за чотирирозрядним форматом.
Рисунок 3.22 – Приклад ділення (+МА) DК на (+МВ)DК за алгоритмом «б»
У зв’язку з цим за алгоритмом «а» крайні незначущі нулі у нерухомому дільнику ВР=[+b3b2b1 000] доцільно відкинути, але, природно, при виконанні арифметичних операцій (3.102) і (3.104) числова змінна ВР=[+b3b2b1] повинна вважатися поліномом:
[+(b3 ×25 + b2 ×24 + b1 ×23)],
де 25, 24, 23 – вага розрядів старшої тріади розширеного формату нерухомого дільника ВР = [+ (b3b2b1 000),].


 частки справедливі співвідношення:
частки справедливі співвідношення: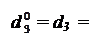
 1, якщо А3 ≥ 0;
1, якщо А3 ≥ 0; = (128 + А4 + ВР3) m128 = (А4
= (128 + А4 + ВР3) m128 = (А4 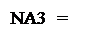
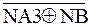 ( 3.85 )
( 3.85 ) початковий стан змінних залежить від значення цифри d3 частки, визначеної у попередньому циклі.
початковий стан змінних залежить від значення цифри d3 частки, визначеної у попередньому циклі.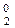 частки потрібно обчислювати за співвідношенням:
частки потрібно обчислювати за співвідношенням: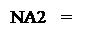
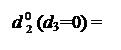
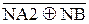 ( 3.91 )
( 3.91 )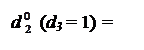
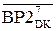 + 1) m128. ( 3.95 )
+ 1) m128. ( 3.95 )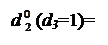
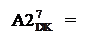
 (А3
(А3  і d
і d 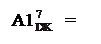
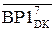 +1)m128 при NA2 = NB; ( 3.99 ) d
+1)m128 при NA2 = NB; ( 3.99 ) d 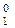 =
= 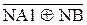 , (3.100)
, (3.100)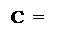 МА – МВ*(d3×22 + d 2×21 + 1), якщо d1= 1;
МА – МВ*(d3×22 + d 2×21 + 1), якщо d1= 1;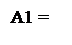
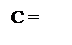
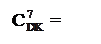 А1
А1 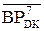 +1)m128 при NA3 = NB; (3.102) d
+1)m128 при NA3 = NB; (3.102) d 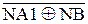 , (3.105)
, (3.105)
 BР
BР 
 (
( 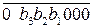 + 1 = 1
+ 1 = 1 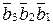 111 + 1 =
111 + 1 =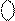
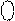 = 1
= 1 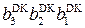 000 = [ 1
000 = [ 1 
 ND
X X X X 0
ND = NAÅNB = 0
ND
X X X X 0
ND = NAÅNB = 0
 ND
ND 
 X X X 0 0
X X X 0 0

 ND
ND 
 X X 0 0 1
X X 0 0 1



 0 0 0 1 1 0 1
0 0 0 1 1 0 1

 NA
NA

 1 1 1 1 1 0 1
1 1 1 1 1 0 1

 0 0 0 0 1 0 1
0 0 0 0 1 0 1

 NA2
NA2

 0 0 0 0 0 0 1
0 0 0 0 0 0 1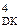


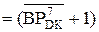 NA =NB
=
NA =NB
= 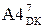
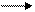 NB BP
NB BP


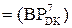 NA4 ≠ NB
=
NA4 ≠ NB
= 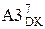
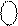
 NB BP
NB BP
 0 0 0 0 1 0 0
0 0 0 0 1 0 0

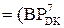 +1) NA3=NB
=
+1) NA3=NB
= 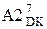
 0 0 0 0 0 1 0
0 0 0 0 0 1 0