Для ілюстрації функціональних особливостей канонічного алгоритму операції ділення доповняльних кодів (DК) побудуємо блок ділення, в якому аргументи і результат визначаються за наступними форматами:
 А
А  = NА a
= NА a 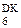 a
a 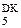 a
a 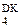 a
a 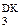 a
a 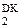 a
a 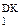 ;
;

 B
B 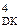 = NB b
= NB b 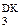 b
b 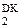 b
b 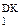 ; D
; D 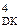 = ND d
= ND d 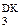 d
d 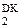 d
d 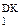 ;
;
 C
C 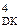 = NC c
= NC c 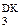 c
c 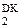 c
c 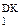 ,
,



 де NA , NB , ND , NC - знак доповняльного коду відповідно діленого, дільника, частки, остачі;
де NA , NB , ND , NC - знак доповняльного коду відповідно діленого, дільника, частки, остачі;
a 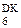 a
a 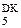 a
a 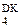 a
a 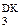 a
a 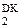 a
a 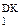 , b
, b 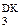 b
b 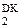 b
b 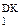 , d
, d 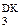 d
d 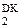 d
d 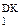 , c
, c 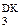 c
c 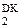 c
c 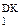 – цифрова частина доповняльного коду відповідного діленого, дільника, частки і остачі.
– цифрова частина доповняльного коду відповідного діленого, дільника, частки і остачі.
Відомо, що за додатних значень частки її зображення в доповняльному і прямому кодах подаються однаково:
 D
D 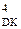 = D
= D 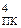 = 0 d3 d2 d1 ( 3.60 )
= 0 d3 d2 d1 ( 3.60 )
де 0 - значення знакового розряду додатної частки;
d3 d2 d1 – значення цифрових розрядів додатної частки у прямому виді.
У зв’язку з цим, для утворення цифрових розрядів доповняльного коду за додатних значень частки достатньо визначити значення цифр частки в пря-мому виді за допомогою будь-якого загального алгоритму операції ділення.
Для від’ємних значень частки прямий і доповняльний код частки пов’язані більш складними співвідношеннями. У цьому випадку, щоб пристосувати загальні алгоритми визначення значень цифр частки в прямому виді до утворення результату в доповняльному коді, спочатку доцільно сформувати обернений до прямих значень рядок цифр частки, тобто обернений код цифрової частини частки, а на завершальному етапі – розшукуваний доповняльний код від’ємної частки. Алгоритм перетворення оберненого коду від’ємної частки в еквівалентний доповняльний код випливає з базових формул визначення оберненого і доповняльного кодів:
D 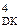 = 15 + D;
= 15 + D;
D 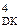 = 16 + D = (15 + D) + 1,
= 16 + D = (15 + D) + 1,
де D – двійковий код від’ємної частки.
Звідси дістанемо:
D 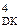 = D
= D 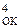 + 1, ( 3.61 )
+ 1, ( 3.61 )
де D 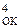 - обернений код від’ємної частки .
- обернений код від’ємної частки .
Таким чином, згідно з (3.61) для обчислення доповняльного коду від’ємної частки D попередньо потрібно визначити інверсні значення цифро-вих розрядів модуля частки, а потім виконати корекцію (виправлення) утвореного оберненого коду шляхом додавання одиниці до його молодших розрядів.
Узагальнюючи (3.60) і (3.61) маємо:
 D
D 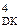 = ND d
= ND d 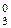 d
d  d
d  + ND, (3.62)
+ ND, (3.62)
де ND = (NA Å NB) – знак результату (частки);
(d 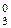 d
d  d
d  ) – цифрові розряди оберненого коду частки;
) – цифрові розряди оберненого коду частки;
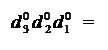
 d3d2d1, якщо ND = 0;
d3d2d1, якщо ND = 0;
 , якщо ND = 1,
, якщо ND = 1,
де (d3d2d1) – цифрові розряди модуля частки ( MD = |D| = d3d2d1);
( 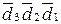 ) – порозрядна інверсія цифрових розрядів модуля частки.
) – порозрядна інверсія цифрових розрядів модуля частки.
Таким чином, до визначення цифр частки як за алгоритмом (3.60), так і за алгоритмом (3.61), спочатку потрібно знайти знак результату на підставі звичайного співвідношення для знаків:
ND = (NA Å NB), ( 3.63 )
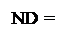
 тобто 1, якщо NA ≠ NB;
тобто 1, якщо NA ≠ NB;
0, якщо NA = NB.
На наступному рівні програми ділення А  на В
на В 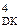 встановлюється можливість переповнення розрядної сітки цифрової частини частки. Для цього, як зазначалося раніше, у пробному циклі обчислюється розшир розрядної сітки частки D. У зв’язку з цим, доповняльний код частки формує-ться у розширеному форматі:
встановлюється можливість переповнення розрядної сітки цифрової частини частки. Для цього, як зазначалося раніше, у пробному циклі обчислюється розшир розрядної сітки частки D. У зв’язку з цим, доповняльний код частки формує-ться у розширеному форматі:
 (DP)
(DP) 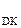 = ND d
= ND d 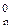 d
d 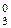 d
d  d
d  + ND, ( 3.64 )
+ ND, ( 3.64 )
 де (d
де (d 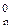 d
d 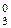 d
d  d
d  ) – цифрова частина розширеного формату оберненого коду частки;
) – цифрова частина розширеного формату оберненого коду частки;
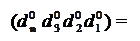 dn d3d2d1, якщо ND = 0; ( 3.65 )
dn d3d2d1, якщо ND = 0; ( 3.65 )
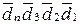 , якщо ND = 1; ( 3.66 )
, якщо ND = 1; ( 3.66 )
d  – розшир частки для виявлення ознаки переповнення розрядної сітки результату;
– розшир частки для виявлення ознаки переповнення розрядної сітки результату;
(DP) 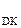 - розширений п’ятипозиційний формат доповняльного коду частки.
- розширений п’ятипозиційний формат доповняльного коду частки.
У залежності від знака частки ND і ознаки переповнення частки (d 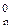 ) у розширеному форматі частки (3.64) можуть формуватися комбінації двійко-вих кодів:
) у розширеному форматі частки (3.64) можуть формуватися комбінації двійко-вих кодів:
ND d 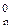 ND
ND
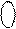
 (DP)
(DP) 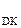 ( d
( d  = 0, D ≥ 0) = 0 0 d
= 0, D ≥ 0) = 0 0 d  d
d  d
d  + 0 ;
+ 0 ;
 ND d
ND d  ND
ND
 (DP)
(DP) 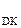 ( d
( d  = 0, D < 0) = 1 1 d
= 0, D < 0) = 1 1 d 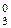 d
d  d
d  + 1 ;
+ 1 ;
ND d 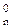 ND
ND
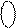
 (DP)
(DP) 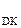 ( d
( d  = 1, D ≥ 0) = 0 1 d
= 1, D ≥ 0) = 0 1 d 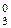 d
d  d
d  + 0 ;
+ 0 ;
 ND d
ND d  ND
ND
(DP) 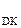 ( d
( d  = 1, D < 0) = 1 0 d
= 1, D < 0) = 1 0 d 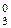 d
d  d
d  + 1 .
+ 1 .
Звідси випливає, що ознаку переповнення оберненого коду частки ППОК у загальному випадку припустимо обчислювати за співвідношенням:
ППОК = (ND Å d 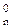 ), ( 3.67 )
), ( 3.67 )
Очевидно, що згідно з властивостями оберненого коду D 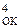 ознака переповнення оберненого коду ППОК не фіксується, якщо значення частки змінюється в замкнутому інтервалі:
ознака переповнення оберненого коду ППОК не фіксується, якщо значення частки змінюється в замкнутому інтервалі:
- 111(-710) ≤ D ≤ +111 (+710).
В доповняльному коді частки обумовленого формату (D 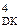 ) перетво-рення розрядної сітки частки не повинно виникати в діапазоні зміни аргумента:
) перетво-рення розрядної сітки частки не повинно виникати в діапазоні зміни аргумента:
- 1000(-810) ≤ D ≤ +111 (+710).
З наведеного випливає, що при утворенні частки D=-1000(-810), тобто за

 ND d
ND d 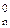 d
d 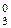 d
d  d
d 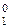 ND d
ND d 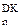 d
d 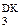 d
d 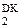 d
d 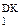
 DР
DР 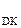 = 1 0 1 1 1 + 1 = 1 1 0 0 0
= 1 0 1 1 1 + 1 = 1 1 0 0 0
 ознака переповнення доповняльного коду ППDК не повинна формуватися за ППОК = ND
ознака переповнення доповняльного коду ППDК не повинна формуватися за ППОК = ND 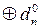 = 1
= 1  0 = 1.
0 = 1.
Таким чином, за від’ємних значень частки у загальному випадку ознака переповнення оберненого коду частки ППОК після формування слушного результату в доповняльному коді на завершальному етапі операції ділення повинна уточнюватися за співвідношенням:
 ППDК = ND
ППDК = ND 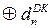 . ( 3.68 )
. ( 3.68 )
Тепер докладно розглянемо алгоритми визначення розширеного п’яти-позиційного формату частки для довільного сполучення знаків діленого А і дільника В.
Спочатку припустімо, що ділене А > 0 (NA=0) і дільник В > 0 (NВ=0).
За цих умов залишок діленого у пробному кроці операції ділення визначається числовими змінними:
А = + МА(6/1); ( 3.69 )
ВР = + МВР(6/1), ( 3.70 )
де А, ВР – відповідно числові змінні діленого і розширеного формату дільника;
МА(6/1), МВР(6/1) = МВ(3/1) 000 – відповідно модулі діленого А і подвійного дільника В;
МВ(3/1) = b3b2b1 – рядок цифр модуля дільника за первинним форматом.
У даному випадку NA = NВ = 0 і знак частки ND = NA Å NВ = 0, тому згідно з (3.65) розшир частки визначається за співвідношенням:
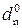 = dn = d4.
= dn = d4.
Як відомо, четвертий розряд (розшир) частки d4 = 1 у тому випадку, коли
МА(6/1) ≥ МВР(6/1). ( 3.71 )
Отже, розшир частки dn = d4 потрібно обчислювати за нерівностями виду:
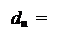
 1, якщо А4 ≥ 0;
1, якщо А4 ≥ 0;
0, якщо А4 < 0, ( 3.72 )
де А4 = [МА(6/1) – МВР(6/1)] – залишок діленого у пробному кроці операції ділення.
Для визначення залишку діленого А4 через доповняльний код 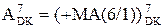 і
і 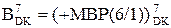 перетворимо (3.72) наступним чином:
перетворимо (3.72) наступним чином:
А4 = (+МА(6/1)) – (+МВР(6/1)).
Тоді згідно з ( 3.68) і (3.69) дістанемо:
А4 = А – ВР. ( 3.73 )
Із цих міркувань випливає, що доповняльний код залишку діленого А4 потрібно обчислювати за співвідношенням: 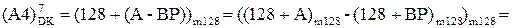
= ( 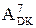 -
- 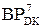 )m128 = (
)m128 = ( 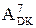 + 128 -
+ 128 - 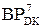 )m128 =
)m128 =
= ( 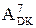 + 127 -
+ 127 - 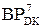 + 1)m128 = (
+ 1)m128 = ( 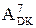 +
+ 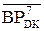 +1)m128. ( 3.74 )
+1)m128. ( 3.74 )
Згідно властивостей доповняльного коду маємо:
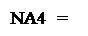
 0, якщо А4 ≥ 0;
0, якщо А4 ≥ 0;
1, якщо А4 < 0, ( 3.75 )
де NA4 – знак числової змінної  .
.
Із урахуванням (3.75) нерівності (3.72) можна подати у вигляді:
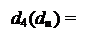
 1, якщо NА4 = 0;
1, якщо NА4 = 0;
0, якщо NА4 = 1. ( 3.76 )
Через те, що при діленні (+МА) на (+МВ) знак дільника NB = 0, зна-чення розширу dn може бути пов’язано зі знаком дільника NB нерівностями виду:
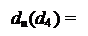
 1, якщо NА4 = NB;
1, якщо NА4 = NB;
0, якщо NА4 ≠ NB.
Звідси дістанемо:
d4 (dn ) = 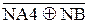 . ( 3.77 )
. ( 3.77 )
Приклади визначення розширу частки d 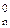 і ознаки переповнення обер-неного коду частки при діленні (+МА)DK на (+МВ)DK подано на рис.3.20-3.21.
і ознаки переповнення обер-неного коду частки при діленні (+МА)DK на (+МВ)DK подано на рис.3.20-3.21.
Припустімо, що обчислення наступної цифри частки d  виконуються зі зсувом вправо дільника, тобто за алгоритмом «б».
виконуються зі зсувом вправо дільника, тобто за алгоритмом «б».
Початковий стан числових змінних, за якими визначається наступна цифра частки d  буде мати вигляд:
буде мати вигляд:
Рисунок 3.20 – Приклад визначення розширу 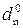 частки
частки
і ознаки ПП частки при діленні (+МА)DK на (+МВ)DK.
Рисунок 3.21 – Приклад визначення одиничних станів розширу 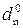


 А
А  = NА a
= NА a 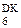 a
a 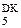 a
a 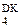 a
a 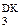 a
a 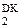 a
a 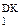 ;
;
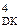 = NB b
= NB b 
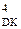 = D
= D  = 0 d3 d2 d1 ( 3.60 )
= 0 d3 d2 d1 ( 3.60 ) + 1, ( 3.61 )
+ 1, ( 3.61 ) D
D 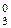 d
d  d
d  + ND, (3.62)
+ ND, (3.62)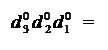
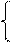 d3d2d1, якщо ND = 0;
d3d2d1, якщо ND = 0;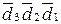 , якщо ND = 1,
, якщо ND = 1,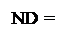
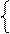 тобто 1, якщо NA ≠ NB;
тобто 1, якщо NA ≠ NB; (DP)
(DP) 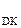 = ND d
= ND d 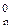 d
d 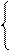 де (d
де (d 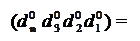 dn d3d2d1, якщо ND = 0; ( 3.65 )
dn d3d2d1, якщо ND = 0; ( 3.65 )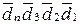 , якщо ND = 1; ( 3.66 )
, якщо ND = 1; ( 3.66 ) – розшир частки для виявлення ознаки переповнення розрядної сітки результату;
– розшир частки для виявлення ознаки переповнення розрядної сітки результату;
 (DP)
(DP)  ND d
ND d 
 ND
ND

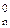 d
d 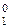 ND d
ND d 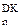 d
d 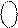
 ознака переповнення доповняльного коду ППDК не повинна формуватися за ППОК = ND
ознака переповнення доповняльного коду ППDК не повинна формуватися за ППОК = ND 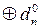 = 1
= 1  0 = 1.
0 = 1. ППDК = ND
ППDК = ND 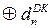 . ( 3.68 )
. ( 3.68 )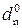 = dn = d4.
= dn = d4.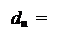
 1, якщо А4 ≥ 0;
1, якщо А4 ≥ 0;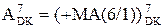 і
і 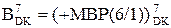 перетворимо (3.72) наступним чином:
перетворимо (3.72) наступним чином: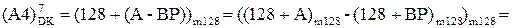
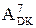 -
- 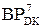 )m128 = (
)m128 = ( 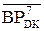 +1)m128. ( 3.74 )
+1)m128. ( 3.74 )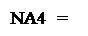
 .
.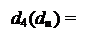
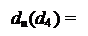
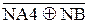 . ( 3.77 )
. ( 3.77 ) виконуються зі зсувом вправо дільника, тобто за алгоритмом «б».
виконуються зі зсувом вправо дільника, тобто за алгоритмом «б».
 X X X X X
X X X X X

 ND
ND X X X X 0
X X X X 0 ND
ND 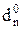
 X X X 0 0
X X X 0 0
 0 0 1 1 0 1 0
0 0 1 1 0 1 0


 NA
NA

 ND
ND

 1 0 1 1 0 0 0
1 0 1 1 0 0 0


 NAM NB=0
NAM NB=0
 о
о

 0 1 0 1 0 0 0
0 1 0 1 0 0 0

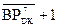 )
) А
А  ВP
ВP 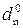 частки
частки
 ND
ND
 X X X X 0
ND = NA Å NB
X X X X 0
ND = NA Å NB
 ND
ND 
 X X X 0 1
X X X 0 1


 о
о 
 = A
= A 
 АDК = 0 110 010
ВPDК= 0 101 000
АDК = 0 110 010
ВPDК= 0 101 000