Операція ділення цілих чисел однакового формату здійснюється за по-рівняно досить складним алгоритмом, оскільки до початку визначення цифр частки здійснюються різного роду перетворення початкового стану опе-рандів. Перевагою блока ділення цілих чисел однакового формату є можли-вість за даним алгоритмом ділення чисел будь-якого формату, одержання результату за тим же форматом і при значущих операндах можливість формувати правильний результат завжди без переповнення розрядної сітки частки.
| PВ
|  РА РА
| 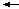 РD РD
|
| 4 3 2 1
| 4 3 2 1
| 4 3 2 1
|
 NB 1 1 1
[+PB(3/4)] NB 1 1 1
[+PB(3/4)] 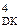 = =
Відновлення
остачі ділення
[+PB(3/1)] 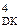 = =
МC =
 NB NB
  ND Å NA=NC ND Å NA=NC

C  = PA(4/1) = = PA(4/1) =
| 0  1 0 1 1 0 1
 +
1 0 0 1 +
1 0 0 1
1 0 1 0

+
0 1 1 1
0 0 0 1
NC 0 0 1
|    ND 1 1 X
d1 = 0 ND 1 1 X
d1 = 0
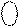 ND 1 1 0 ND 1 1 0
D 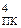
|
Рисунок 3.13,б – Приклад роботи блока ділення чисел за алгоритмом «а» без відновлення залишку (визначення d1, модуля остачі MС і С 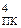 )
)
Ділення чисел у прямих кодах однакової довжини зводиться до ви-значення знакових розрядів і модулів частки МD та остачі МС, довжина яких збігається з форматом модулів діленого і дільника.
Згідно з правилами алгебри знаки частки D і остачі С визначаються на підставі виразів:
ND = NA Å NB; NC = NA = NB Å ND.
Зазначимо також, що до визначення цифрових розрядів частки модулі дільника МВ і діленого МА аналізуються на нуль: якщо МВ=0, то в блоці ділення фіксується аварійне переповнення частки і програма ділення аварійно переривається; за умови, коли МВ ≠ 0 і МА = 0, частці присвоюється нульове значення і програма ділення закінчується звичайним способом.
Якщо МВ ≠ 0 і МА ≠ 0, то на наступному рівні програми ділення визна-чаються цифри частки і остачі на основі модулів операндів А і В.
Очевидно, що при діленні, наприклад n–розрядного модуля діленого МА на n-розрядний модуль дільника МВ, довжина цілої частини частки (кількість значущих цифр частки) може змінюватися в межах від n розрядів до одного розряду. У кожному конкретному випадку довжина частки пов’язана з довжиною діленого і дільника співвідношенням:
HD

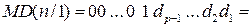
HA


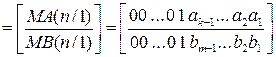 ( 3.44 )
( 3.44 )
HB
де [ ] – ціла частина відповідного коду;
МD(n/1), МA(n/1), МB(n/1) – відповідно модулі частки D, діленого А і дільника В за n-розрядним форматом;
k, m – відповідно довжина модуля діленого МА(n/1) і модуля дільника МВ(n/1), тобто кількість значущих цифр діленого МА і дільника МВ;
НА = (n – k), НВ = (n – m) – відповідно кількість нульових розрядів у старших позиціях n–розрядного полінома діленого МA(n/1) і дільника МB(n/1) ;
р – кількість значущих цифр модуля частки МD(n/1);
НD = (n–р) – кількість нульових цифр у старших позиціях n–розрядного полінома частки МD(n/1).
Слід зазначити, що у випадку, коли
НВ < НА , ( 3.45 )
справедливе співвідношення:
МА(n/1) < МВ(n/1).
Тому у цьому випадку слушне значення результату має нульове значення:
 n
n
МD(n/1) = 00 … 0 .
У зв’язку з цим на першому рівні програми ділення МА(n/1) на МВ(n/1) передусім перевіряється логічна умова (3.45). Якщо нерівність (3.45) виконується, то модулю частки МD(n/1) присвоюється нульове значення і мікропрограма ділення МА(n/1) на МВ(n/1) закінчується звичайним способом. Якщо нерівність (3.45) не виконується, то формується перехід на послідовність мікрооперацій, які призначені для формування цілої частини модуля частки МD(n/1) ≠ 0. Алгоритм визначення цифр цілої частини частки МD(n/1) будується на основі наступного перетворення співвідношення (3.44):
НА

 МD(n/1)
МD(n/1) 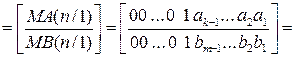
НВ
НА НА




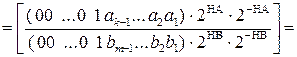
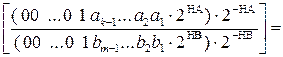
НВ НА НВ


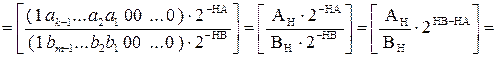
НВ
НD (НВ- НA) НD (НВ- НA+1)




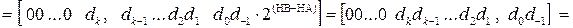
НD (НВ- НA+1)

 =
= 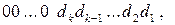 ( 3.46 )
( 3.46 )
де k = (НВ –НА + 1) – можлива довжина цілої частини частки МD(n/1), тобто найбільш можлива кількість значущих цифр модуля частки МD(n/1);
HD = (n + НА – НВ - 1) – найменш можлива кількість нульових цифр у старших позиціях частки МD(n/1);
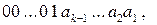
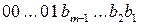 - первинний стан відповідно модулів МА(n/1) і МВ(n/1); НА
- первинний стан відповідно модулів МА(n/1) і МВ(n/1); НА
 АН =
АН = 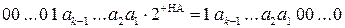 ,
,
НВ
 ВН=
ВН= 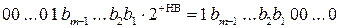 - так звані знормовані коди відповідно модуля діленого А і модуля дільника В, які отримані логічним зсувом вліво модуля діленого на НА розрядів і модуля дільника на НВ розрядів;
- так звані знормовані коди відповідно модуля діленого А і модуля дільника В, які отримані логічним зсувом вліво модуля діленого на НА розрядів і модуля дільника на НВ розрядів;
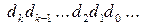 - повний формат частки при діленні знормованих кодів АН на ВН;
- повний формат частки при діленні знормованих кодів АН на ВН;
k,k-1,k-2, …, 2, 1 – номери визначуваних розрядів цілої частини частки.
Таким чином, у загальному випадку згідно з (3.46) за операцією діленняАН на ВН підлягають визначенню цифри відповідно в k,k-1,k-2,…,2,1 позиціях повної частки, тобто цифри двійкового полінома:
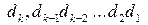 =
=
= 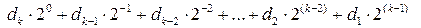 ( 3.47 )
( 3.47 )
де k = (НВ –НА + 1) – номер позиції найстаршого розряду двійкового коду частки МD(n/1), який може бути значущим.
Значення найстаршої цифри частки у k –му розряді згідно з (3.47) визначаються нерівністями виду:
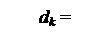
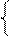 1, якщо АН - ВН ≥ 0,
1, якщо АН - ВН ≥ 0,
0, якщо АН - ВН < 0.
З цього випливає наступний алгоритм визначення цифри dk :
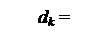
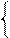 1, якщо Аk ≥ 20,
1, якщо Аk ≥ 20,
0, якщо Аk < 20. ( 3.48 )
де Аk=(АН–Вk) – частковий залишок знормованого діленого АН= МА×2+НВ після віднімання знормованого дільника Вk = ВH = МВ×2+НВ;
k = (НВ –НА + 1) – номер позиції найстаршої цифри частки.
За умови, коли dk = 1, залишок Аk=(АН–Вk ) ≥ 0 і наступна цифра частки dk-1 згідно з (3.47) повинна визначатися нерівностями виду:
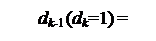
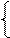 1, якщо АН - ВН ≥ (20 + 2-1),
1, якщо АН - ВН ≥ (20 + 2-1),
0, якщо АН - ВН < (20 + 2-1).
Очевидно, що ці залежності можна подати у вигляді:
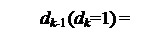
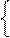 1, якщо (АН - ВН ×20 - ВН ×2-1) ≥ 0,
1, якщо (АН - ВН ×20 - ВН ×2-1) ≥ 0,
0, якщо (АН - ВН ×20 - ВН ×2-1) < 0.
З урахуванням (3.48) маємо:
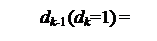
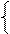 1, якщо Аk-1 ≥ 0,
1, якщо Аk-1 ≥ 0,
0, якщо Аk-1 < 0, ( 3.49 )
де Аk-1 = (Аk - Вk-1) ; Вk-1 = Вk /2; Вk = ВН ×20.
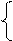 У тому випадку, коли dk=0, залишок Аk=(АН–Вk) < 0 і наступна цифра частки dk-1 згідно з (3.47) повинна визначатися нерівностями виду:
У тому випадку, коли dk=0, залишок Аk=(АН–Вk) < 0 і наступна цифра частки dk-1 згідно з (3.47) повинна визначатися нерівностями виду:
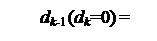 1, якщо АН - ВН ≥ 2-1,
1, якщо АН - ВН ≥ 2-1,
0, якщо АН - ВН < 2-1.
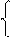 Нерівності можна подати у вигляді :
Нерівності можна подати у вигляді :
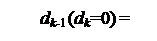 1, якщо (АН - ВН /2) ≥ 0,
1, якщо (АН - ВН /2) ≥ 0,
0, якщо (АН - ВН /2) < 0.
Згідно з (3.48) справедливі співвідношення АН = (Аk + Вk), ВН /2 = ВК/2.
Тоді нерівності dk-1 (dk=0) можна подати у такому вигляді:
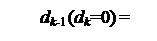
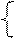 1, якщо (Аk + Вk) – ВК/2 ≥ 0,
1, якщо (Аk + Вk) – ВК/2 ≥ 0,
0, якщо (Аk + Вk) – ВК/2 < 0.
Звідси дістанемо:
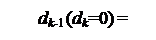
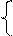 1, якщо Аk -1 ≥ 0,
1, якщо Аk -1 ≥ 0,
0, якщо Аk-1 < 0, ( 3.50 )
де Аk-1 = (Аk + Вk) – ВК/2;
(Аk+Вk) – корекція (виправлення) від’ємного значення залишку Аk при dk=0 (оператор відновлення попереднього додатного залишку діленого АН).
Сукупність операцій (3.48) ÷ (3.50) визначають алгоритм «б» ділення модулів прямого коду чисел з відновленням від’ємних значень часткових залишків. Можливе апаратне рішення побудованого алгоритму подано на рис.3.14.
Блок ділення містить:
- реверсивні зсувні регістри А і В для запису з шини даних відповідно діленого А  і дільника В
і дільника В  в прямих кодах;
в прямих кодах;
- зсувний регістр D для нагромадження цифр частки;
- суматор SM для створення часткових залишків діленого;
- лічильники СТ і СТС для визначення відповідно ознаки завершення операції ділення знормованих модулів діленого і дільника та кількості нульових цифр у старших розрядах остачі С;
- комутатор КВ для формування прямого або інверсного коду дільника на інформаційних входах суматора SM.
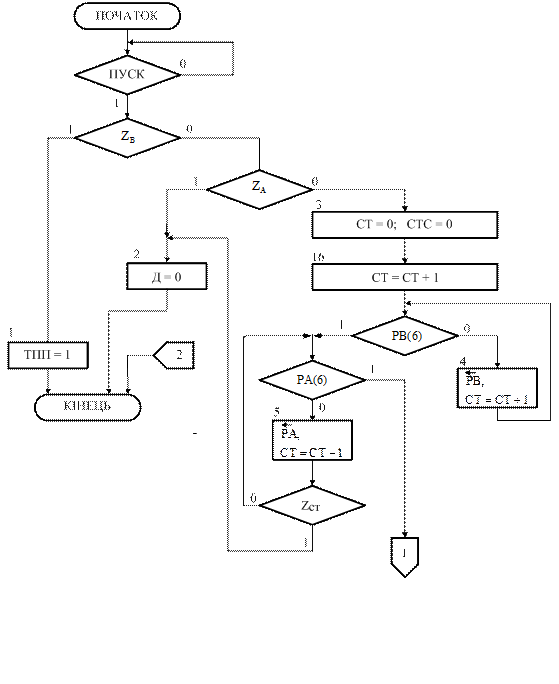
Можлива мікропрограма блока ділення АПК на ВПК (рис.3.14) подана на рис.3.15.
Знормовані модулі діленого і дільника формуються зсувом регістрів А і В вліво до появи одиниці в найстарших цифрових розрядах регістрів А і В (вершини 4 і 5). При цьому паралельно в лічильниках СТ і СТС нагро-маджуються відповідно кількість циклів операції ділення, тобто стан k=(НВ+1)–НА і нульових цифр у старших розрядах регістра А, тобто значення НА.
Зазначимо що, якщо в процесі визначення коду k в лічильнику СТ формується ознака нуля (СТ=0), то результату присвоюється нульове значен-ня і операція ділення блокується (у цьому випадку HB<HA і ціла частина частки повинная мати нульове значення).
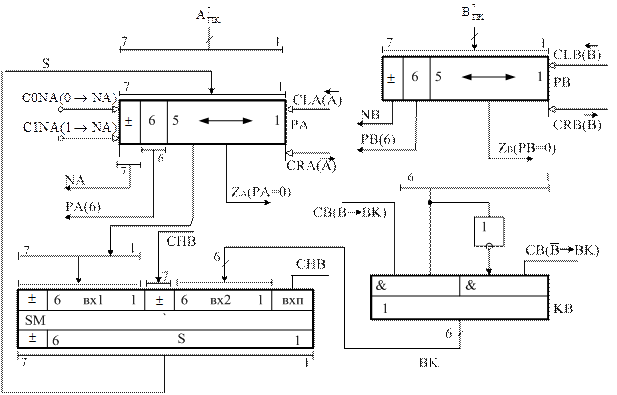
Рисунок 3.14,а – Схема блокa ділення А  на В
на В  за алгоритмом «б»
за алгоритмом «б»
з відновленням залишку ( функціональна блок-схема регістрів А, В
і суматора SM)
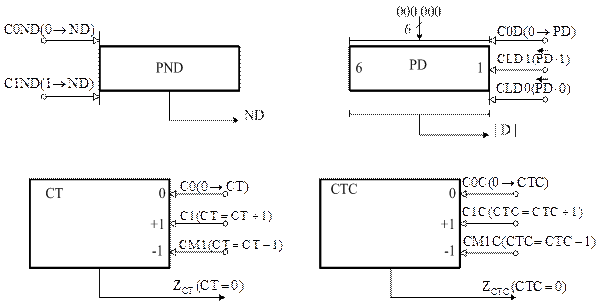
Рисунок 3.14,б – Схема блокa ділення А  на В
на В  за алгоритмом
за алгоритмом
«б» з відновленням залишку (функціональна блок-схема регістра D,
лічильників СТ і СТС)
Рисунок 3.15,а – Початок мікропрограми блока ділення А  на В на В  (рис.3.14) за алгоритмом «б» з відновленням залишку (рис.3.14) за алгоритмом «б» з відновленням залишку
| |
 Після завершення операції ділення (за k > 0) для формування слушного модуля остачі МС регістр А зсувається на НА розрядів вліво (за вмістом СТС (вершина 12)), остача С розміщується в регістрі А на місці старших розрядів діленого, а частка – в регістрі D. Знак частки записується в регістр PND. Якщо останній залишок діленого А1 (за яким визначається молодша цифра d1 частки) є від’ємним, остача А1 коректується (виправляється) додаванням модуля дільника (вершина 11).
Після завершення операції ділення (за k > 0) для формування слушного модуля остачі МС регістр А зсувається на НА розрядів вліво (за вмістом СТС (вершина 12)), остача С розміщується в регістрі А на місці старших розрядів діленого, а частка – в регістрі D. Знак частки записується в регістр PND. Якщо останній залишок діленого А1 (за яким визначається молодша цифра d1 частки) є від’ємним, остача А1 коректується (виправляється) додаванням модуля дільника (вершина 11).
Приклад роботи блока ділення (рис.3.14) за алгоритмом «б» з відновленням залишку подано на рис.3.16.
Зазначимо, що модуль дільника при нормалізації зсувається вліво на НВ розрядів, а в циклі ділення вправо на (НВ – НА) розрядів, тобто на меншу кількість розрядів, тому додаткові розряди в регістрі В для зберігання цифр дільника при його зсуві вправо за алгоритмом “б” в схемі не потрібні.
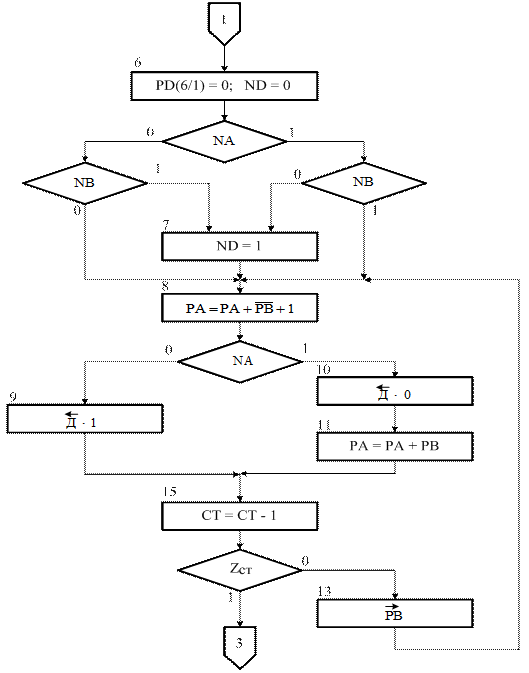
Рисунок 3.15,б – Продовження мікропрограми блока ділення А 
на В  (рис.3.14) за алгоритмом «б» з відновленням залишку
(рис.3.14) за алгоритмом «б» з відновленням залишку
Нерівності (3.50) для визначення dk-1 цифри частки за умови, коли dk=0 і А k= (АH– ВH) < 0, можна подати у вигляді:
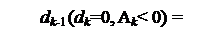
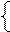 1, якщо (Аk – ВК/2) ≥ 0;
1, якщо (Аk – ВК/2) ≥ 0;
0, якщо (Аk – ВК/2)< 0, ( 3.51 )
де Аk= (АH– ВН) – частковий залишок для визначення dk цифри частки, який за dk=0 являє собою від’ємне число;
ВH = ВК – стан дільника для визначення найстаршої цифри dk частки за знормованим станом дільника.
Узагальнюючи (3.50 ) і (3.51), маємо:
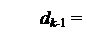
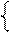 1, якщо Аk-1 ≥ 0;
1, якщо Аk-1 ≥ 0;
0, якщо Аk-1 < 0, ( 3.52 )
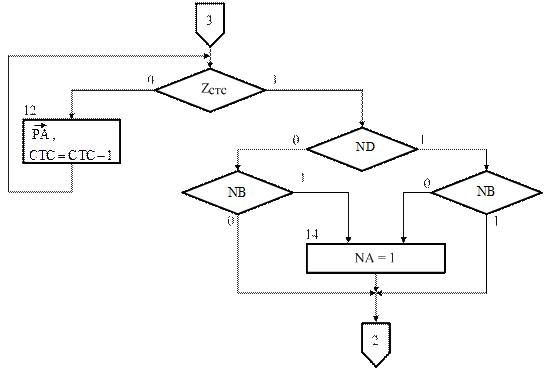
Рисунок 3.15,в – Завершення мікропрограми блока ділення А 
на В  (рис.3.14) за алгоритмом «б» з відновленням залишку
(рис.3.14) за алгоритмом «б» з відновленням залишку
Рисунок 3.16,а – Приклад роботи блока ділення А  на В
на В  (рис.3.14)
(рис.3.14)
за алгоритмом «б» з відновленням залишку (визначення знака ND i
позиції d3 частки)
PD (D  ) )
| PA (А  ) )
|    PB (В PB (В  ) )
| CT
| CTC
|
 (A3) (A3)  = =
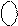 ND 0 0 0 0 0 1
[-PB(6/1)] ND 0 0 0 0 0 1
[-PB(6/1)]  =
(A2) =
(A2)  = =
 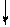 d2=0 d2=0
ND 0 0 0 0 1 0
[+PB(6/1)]  = =
(A3)  = =
[- PB(6/1)]  = =
(A1)  = =
 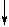 d1=1 d1=1
 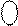 ND 0 0 0 1 0 1 ND 0 0 0 1 0 1
    Å Å
NB
|  0 0 0 1 1 0 0 0 0 0 1 1 0 0
1 1 0 1 1 0 0
1 1 1 1 0 0 0
0  0 1 0 1 0 0 0 1 0 1 0 0
0  0 0 1 1 0 0 0 0 1 1 0 0
 1 1 1 0 1 1 0 1 1 1 0 1 1 0
 0 0 0 0 0 1 0 0 0 0 0 0 1 0
  HA HA
0 0 0 0 0 0 1
 NC 0 0 0 0 0 1 NC 0 0 0 0 0 1
|  0 1 0 1 0 0 0
BH = B3 0 1 0 1 0 0 0
BH = B3
 NB 0 1 0 1 0 0 NB 0 1 0 1 0 0
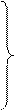 B2 = B3|2 B2 = B3|2
Відновлення
залишку
(A2) 
 NB 0 0 1 0 1 0 NB 0 0 1 0 1 0
B1 = B2|2
= |C| × 2HA
= |C|
= C 
| k=3
| HA=1
|
Рисунок 3.16,б – Приклад роботи блока ділення А  на В
на В  (рис.3.14)
(рис.3.14)
за алгоритмом «б» з відновленням залишку ( визначення позицій d2, d1
частки і остачі C  )
)
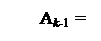
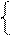 де (Аk – Вk -1) , якщо Аk ≥ 0; (Аk + Вk -1), якщо Аk < 0,
де (Аk – Вk -1) , якщо Аk ≥ 0; (Аk + Вk -1), якщо Аk < 0,
Аk – частковий залишок діленого для визначення цифри dk частки;
Вk-1 = ВК/2 - стан дільника для визначення dk-1 цифри частки;
ВК = ВН – стан знормованого дільника для визначення dk цифри частки.
Співвідношення (3.52) визначають алгоритм «б» (тобто алгоритм із зсувом вправо дільника В) без відновлення попереднього від’ємного залишку діленого. Очевидно, що за таким методом значно підвищується швидкодія блока ділення за рахунок вилучення в програмі ділення мікрооперації (такту) відновлення від’ємного значення вмісту регістра А. Приклад ділення A  на В
на В  за алгоритмом «б» без відновлення залишку подано на рис.3.17.
за алгоритмом «б» без відновлення залишку подано на рис.3.17.
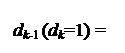 Згідно з (3.49) операцію формування цифри dk-1 частки за умови, коли dk =1, можна подати у вигляді:
Згідно з (3.49) операцію формування цифри dk-1 частки за умови, коли dk =1, можна подати у вигляді:
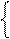 1, якщо (2×Аk – ВН) ≥ 0;
1, якщо (2×Аk – ВН) ≥ 0;
0, якщо (2×Аk – ВН) < 0.
D 
| А 
|    В В 
| CT
| CTC
|
 X X X X X X X X X X X X X X
  ND Å ND Å
ND 0 0 0 0 0 0
(-B4)  = =
(A4)  = =
 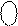 d4=1 d4=1
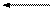  ND 0 0 0 0 0 1 ND 0 0 0 0 0 1
(A3)  = =
 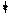  d3=0 d3=0
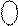 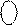  ND 0 0 0 0 1 0 ND 0 0 0 0 1 0
(A2)  = =
  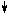 d2=0 d2=0
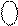 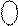   ND 0 0 0 1 0 0 ND 0 0 0 1 0 0
(A1)  = =
    d1=1 d1=1
   ND 0 0 1 0 0 1 ND 0 0 1 0 0 1
    Å Å
NВ
|  NA 1 0 1 1 1 0 NA 1 0 1 1 1 0
 НА = 0 НА = 0
0 1 0 1 1 1 0
1  0 1 1 0 0 0 0 1 1 0 0 0

0  0 0 0 1 1 0 0 0 0 1 1 0

1 1 0 1 1 0 0
 
1  1 1 0 0 1 0 1 1 0 0 1 0
0 0 0 1 0 1 0
 1 1 1 1 1 0 0 1 1 1 1 1 0 0
 0 0 0 0 1 0 1 0 0 0 0 1 0 1
0 0 0 0 0 0 1
NС 0 0 0 0 0 1
|   NB 0 0 0 1 0 1 NB 0 0 0 1 0 1
 HB = 3 HB = 3
 NB 1 0 1 0 0 0 NB 1 0 1 0 0 0
BH=BK=B4
 NB 0 1 0 1 0 0 NB 0 1 0 1 0 0
 B3 = B4|2 B3 = B4|2

 NB 0 0 1 0 1 0 NB 0 0 1 0 1 0
 B2 = B3|2 B2 = B3|2

 NB 0 0 0 1 0 1 NB 0 0 0 1 0 1
B1 = B2|2
=|C|
= C7ПК
| k=HB-
-HA+1 =3+1=
= 4
| HA=0
|
Рисунок 3.17 – Приклад ділення A  на В
на В  за алгоритмом «б»
за алгоритмом «б»
без відновлення залишку
 Звідси дістанемо:
Звідси дістанемо:
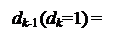 1, якщо Аk-1 ≥ 0;
1, якщо Аk-1 ≥ 0;
0, якщо Аk-1 < 0, ( 3.53 )
де Аk-1=(2×Аk - ВН) - частковий залишок діленого за формою «а» (із зсувом вліво діленого А і нерухомому дільнику В) для визначення цифри dk-1 частки; Аk = (АН - ВН).
Згідно з (3.50) за умови, коли dk=0 і Аk=(АН - ВН) < 0, операцію формування цифри dk-1 частки можна подати у вигляді:
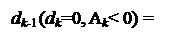
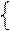 1, якщо (2×АН – ВН) ≥ 0;
1, якщо (2×АН – ВН) ≥ 0;
0, якщо (2×АН – ВН) < 0. ( 3.54 )
З урахуванням того, що знормоване значення діленого АН = (Аk + ВН), нерівності (3.54) можна подати у вигляді:
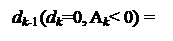
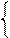 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;
0, якщо А k-1 < 0. ( 3.55 )
де А k-1 = [2(Аk + ВН) – ВН] – частковий залишок діленого за формою «а» для визначення цифри dk-1 частки;
(Аk + ВН) – оператор відновлення попереднього від’ємного залишку АК.
Узагальнюючи (3.54) і (3.55) маємо:
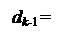
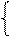 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;
0, якщо А k-1 < 0, ( 3.56 )
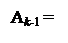
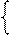 де (2×А k – ВН), якщо А k ≥ 0;
де (2×А k – ВН), якщо А k ≥ 0;
[2×(А k + ВН) – ВН], якщо А k < 0; ( 3.57 )
(АН - ВН) – частковий залишок знормованих діленого і дільника, який визначає попередню цифру dk частки.
Залежності (3.56) і (3.57) описують правила формування цифр у всіх молодших позиціях частки на основі часткових залишків за формою «а» з відновленням попередніх від’ємних залишків.
Приклад ділення A  на В
на В  за алгоритмом «а» з відновленням залиш-ку подано на рис.3.18.
за алгоритмом «а» з відновленням залиш-ку подано на рис.3.18.
D 
|   А А 
| В 
| CT
| CTC
|
| 7 6 5 4 3 2 1
| 7 6 5 4 3 2 1
| 7 6 5 4 3 2 1
| 3 2 1
| 3 2 1
|
 X X X X X X X X X X X X X X
  ND Å ND Å
ND 0 0 0 0 0 0
  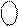 d4 d4
 ND 0 0 0 0 0 1 ND 0 0 0 0 0 1
 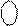  d3 d3
  ND 0 0 0 0 1 0 ND 0 0 0 0 1 0
|   NA 0 1 1 1 1 0 NA 0 1 1 1 1 0
 НА = 1 НА = 1
0 0 1 1 1 1 0
 НА НА
 0 1 1 1 1 0 0 0 1 1 1 1 0 0
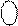
1 0 1 0 0 0 0
 
0 0 0 1 1 0 0
 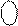
0 0 1 1 0 0 0
1 0 1 0 0 0 0
1 1 0 1 0 0 0
 0 1 1 0 0 0 0 0 1 1 0 0 0 0
0 0 1 1 0 0 0
|   NB 0 0 0 0 1 1 NB 0 0 0 0 1 1
 НВ = 4 НВ = 4
  НВ НВ
 NB 1 1 0 0 0 0
BH
= (-ВН) NB 1 1 0 0 0 0
BH
= (-ВН)  = (A4)
= (A4) 
 = A4
= (-ВН) = A4
= (-ВН) 
= (A3)  Віднов- Віднов-
лення
= (+ВН)  залишку залишку
 = A4 = A4
| k=HB-
-HA+1 =4-1+1
= 4
| HВ=4
|
Рисунок 3.18,а – Приклад ділення A  на В
на В  за алгоритмом «а»
за алгоритмом «а»
з відновленням залишку (визначення ND, d4 i d3 )
| D7ПК
|   А7ПК А7ПК
| В7ПК
| CT
| CTC
|
   ND 0 0 0 0 1 0
ND 0 0 0 0 1 0
   d2 d2
  ND 0 0 0 1 0 1 ND 0 0 0 1 0 1
d2 = 1
 d1 d1
 ND ND  0 0 1 0 1 0 0 0 1 0 1 0
 
     Å NC Å NC
 NВ NВ
|  0 0 1 1 0 0 0
0 0 1 1 0 0 0
0  1 1 0 0 0 0 1 1 0 0 0 0
1 0 1 0 0 0 0
 
0 0 0 0 0 0 0
0 0 0 0 0 0 0
 1 0 1 0 0 0 0 1 0 1 0 0 0 0
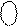 1 0 1 0 0 0 0 1 0 1 0 0 0 0
0 1 1 0 0 0 0
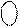 0 0 0 0 0 0 0 0 0 0 0 0 0 0
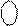  HB HB
0 0 0 0 0 0 0
 NC 0 0 0 0 0 0 NC 0 0 0 0 0 0
|
 = A4 = A4
 2p
= A4
= (-ВН) 2p
= A4
= (-ВН)  = (A2)
= (A2) 
 1p
= A2
= (-ВН) 1p
= A2
= (-ВН)  = (A1)
= (A1)  = (+ВН)
= (+ВН) 
= |C|НВ
= |С|
= C 
| k=HB-
-HA+1 =4-1+1
= 4
| HВ=4
|
Рисунок 3.18,б – Приклад ділення A  на В
на В  за алгоритмом «а» з відновленням залишку (визначення d2, d1, С і C
за алгоритмом «а» з відновленням залишку (визначення d2, d1, С і C  )
)
Зазначимо, що модуль діленого А зсувається вліво на НА розрядів при його нормалізації і потім на (k-1) розряд вліво при визначенні (k-1) молодших розрядів частки (dk-1, dk-2, … , d2, d1). Таким чином, загалом модуль діленого А у блоці ділення за алгоритмом «а» зсувається вліво на [HA+(k-1)] = =[HA+(HB-HA+1)-1)]=HB розрядів. У зв’язку з цим, для формування слуш-ного формату модуля остачі МС останній частковий залишок А1 потрібно денормалізувати на НВ розрядів (рис.3.18).
Cукупність нерівностей (3.57) можна перетворити і записати у вигляді:
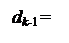
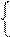 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;
0, якщо А k-1 < 0, ( 3.58 )

| <== попередня лекція |
| |
наступна лекція ==> |
| Мак-Сорлі | | | Довжини на доповняльні коди одинарного формату 1 страница |


 РА
РА
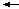 РD
РD
 NB 1 1 1
[+PB(3/4)]
NB 1 1 1
[+PB(3/4)] 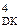 =
=
 NB
NB
 ND Å NA=NC
ND Å NA=NC
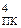 = PA(4/1) =
= PA(4/1) = 1 0 1
1 0 1
 +
1 0 0 1
+
1 0 0 1



 ND 1 1 X
d1 = 0
ND 1 1 X
d1 = 0
 ND 1 1 0
ND 1 1 0

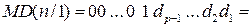

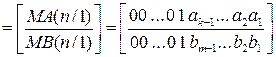 ( 3.44 )
( 3.44 ) n
n
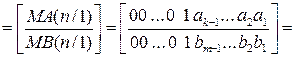

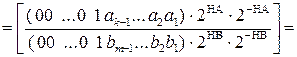
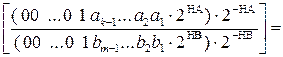

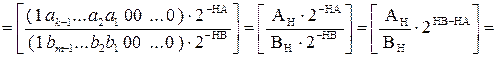




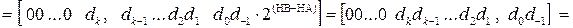

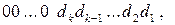 ( 3.46 )
( 3.46 )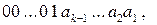
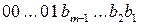 - первинний стан відповідно модулів МА(n/1) і МВ(n/1); НА
- первинний стан відповідно модулів МА(n/1) і МВ(n/1); НА АН =
АН = 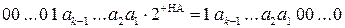 ,
,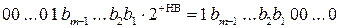 - так звані знормовані коди відповідно модуля діленого А і модуля дільника В, які отримані логічним зсувом вліво модуля діленого на НА розрядів і модуля дільника на НВ розрядів;
- так звані знормовані коди відповідно модуля діленого А і модуля дільника В, які отримані логічним зсувом вліво модуля діленого на НА розрядів і модуля дільника на НВ розрядів;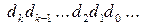 - повний формат частки при діленні знормованих кодів АН на ВН;
- повний формат частки при діленні знормованих кодів АН на ВН;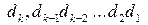 =
=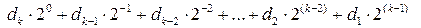 ( 3.47 )
( 3.47 )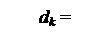
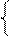 1, якщо АН - ВН ≥ 0,
1, якщо АН - ВН ≥ 0,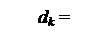
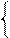 1, якщо Аk ≥ 20,
1, якщо Аk ≥ 20,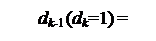
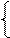 1, якщо АН - ВН ≥ (20 + 2-1),
1, якщо АН - ВН ≥ (20 + 2-1),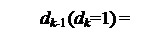
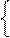 1, якщо (АН - ВН ×20 - ВН ×2-1) ≥ 0,
1, якщо (АН - ВН ×20 - ВН ×2-1) ≥ 0,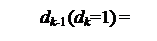
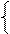 1, якщо Аk-1 ≥ 0,
1, якщо Аk-1 ≥ 0,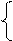 У тому випадку, коли dk=0, залишок Аk=(АН–Вk) < 0 і наступна цифра частки dk-1 згідно з (3.47) повинна визначатися нерівностями виду:
У тому випадку, коли dk=0, залишок Аk=(АН–Вk) < 0 і наступна цифра частки dk-1 згідно з (3.47) повинна визначатися нерівностями виду: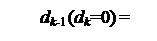 1, якщо АН - ВН ≥ 2-1,
1, якщо АН - ВН ≥ 2-1,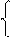 Нерівності можна подати у вигляді :
Нерівності можна подати у вигляді :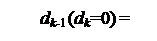 1, якщо (АН - ВН /2) ≥ 0,
1, якщо (АН - ВН /2) ≥ 0,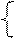 1, якщо (Аk + Вk) – ВК/2 ≥ 0,
1, якщо (Аk + Вk) – ВК/2 ≥ 0,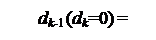
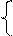 1, якщо Аk -1 ≥ 0,
1, якщо Аk -1 ≥ 0, і дільника В
і дільника В 

 Після завершення операції ділення (за k > 0) для формування слушного модуля остачі МС регістр А зсувається на НА розрядів вліво (за вмістом СТС (вершина 12)), остача С розміщується в регістрі А на місці старших розрядів діленого, а частка – в регістрі D. Знак частки записується в регістр PND. Якщо останній залишок діленого А1 (за яким визначається молодша цифра d1 частки) є від’ємним, остача А1 коректується (виправляється) додаванням модуля дільника (вершина 11).
Після завершення операції ділення (за k > 0) для формування слушного модуля остачі МС регістр А зсувається на НА розрядів вліво (за вмістом СТС (вершина 12)), остача С розміщується в регістрі А на місці старших розрядів діленого, а частка – в регістрі D. Знак частки записується в регістр PND. Якщо останній залишок діленого А1 (за яким визначається молодша цифра d1 частки) є від’ємним, остача А1 коректується (виправляється) додаванням модуля дільника (вершина 11).

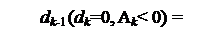
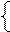 1, якщо (Аk – ВК/2) ≥ 0;
1, якщо (Аk – ВК/2) ≥ 0;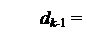
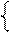 1, якщо Аk-1 ≥ 0;
1, якщо Аk-1 ≥ 0;


 PB (В7ПК)
PB (В7ПК)
 7 6 5 4 3 2 1
7 6 5 4 3 2 1
 7 6 5 4 3 2 1
7 6 5 4 3 2 1
 ND d6d5d4 d3d2d1
ND d6d5d4 d3d2d1
 X X X X X X X
X X X X X X X

 Å
Å


 ND 00 000 |D|=0
ND 00 000 |D|=0 =
= d3=1
d3=1
 ND 0 0 0 0 0 1
ND 0 0 0 0 0 1 NA 0 1 1 0 1 0
NA 0 1 1 0 1 0
 HA=1
HA=1
 HA
HA
 1 1 0 1 0 0
1 1 0 1 0 0 0 1 1 0 0 0
0 1 1 0 0 0 0 0 0 1 1 0 0
0 0 0 1 1 0 0

 NB 0 0 0 1 0 1
NB 0 0 0 1 0 1
 HB=3
HB=3
 HB
HB
 (A3)
(A3) 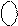 ND 0 0 0 0 0 1
[-PB(6/1)]
ND 0 0 0 0 0 1
[-PB(6/1)] 
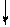 d2=0
d2=0




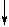 d1=1
d1=1






 Å
Å

 0 0 1 1 0 0
0 0 1 1 0 0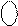
 1 1 1 0 1 1 0
1 1 1 0 1 1 0 HA
HA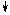
 NC 0 0 0 0 0 1
NC 0 0 0 0 0 1 0 1 0 1 0 0 0
BH = B3
0 1 0 1 0 0 0
BH = B3


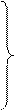 B2 = B3|2
B2 = B3|2

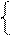 де (Аk – Вk -1) , якщо Аk ≥ 0; (Аk + Вk -1), якщо Аk < 0,
де (Аk – Вk -1) , якщо Аk ≥ 0; (Аk + Вk -1), якщо Аk < 0,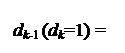 Згідно з (3.49) операцію формування цифри dk-1 частки за умови, коли dk =1, можна подати у вигляді:
Згідно з (3.49) операцію формування цифри dk-1 частки за умови, коли dk =1, можна подати у вигляді: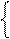 1, якщо (2×Аk – ВН) ≥ 0;
1, якщо (2×Аk – ВН) ≥ 0;
 X X X X X X X
X X X X X X X



 d4=1
d4=1
 ND 0 0 0 0 0 1
ND 0 0 0 0 0 1
 d3=0
d3=0
 ND 0 0 0 0 1 0
ND 0 0 0 0 1 0

 d2=0
d2=0

 d1=1
d1=1




 Å
Å НА = 0
НА = 0

 0 0 0 1 1 0
0 0 0 1 1 0






 B3 = B4|2
B3 = B4|2
 Звідси дістанемо:
Звідси дістанемо: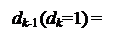 1, якщо Аk-1 ≥ 0;
1, якщо Аk-1 ≥ 0;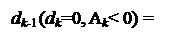
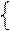 1, якщо (2×АН – ВН) ≥ 0;
1, якщо (2×АН – ВН) ≥ 0;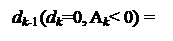
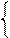 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;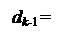
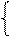 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;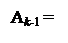
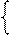 де (2×А k – ВН), якщо А k ≥ 0;
де (2×А k – ВН), якщо А k ≥ 0; А
А 
 d4
d4 ND 0 0 0 0 0 1
ND 0 0 0 0 0 1


 НА
НА


 = A4
= (-ВН)
= A4
= (-ВН) 

 NВ
NВ
 1 0 1 0 0 0 0
1 0 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 NC 0 0 0 0 0 0
NC 0 0 0 0 0 0 2p
= A4
= (-ВН)
2p
= A4
= (-ВН)  1p
= A2
= (-ВН)
1p
= A2
= (-ВН) 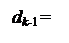
 1, якщо А k-1 ≥ 0;
1, якщо А k-1 ≥ 0;