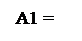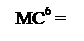У пристроях множення чисел за груповим, наприклад, двопозиційним алгоритмом Мак-Сорлі у кожному циклі множення чисел виконується аналіз трьох цифр множника, які утворюють поточна пара Х2Х3 і молодша цифра Х1 старшої пари (рис.2.26). При цьому молодша цифра Х3 поточної пари умовно за Мак-Сорлі завжди вважається нулем. Комбінація цифр Х1 Х2 вказаної тріади множника подається кодом Бута2. Молодша цифра Х3 наймолодшої групи Х2Х3 множника використовується для виправлення (корекції) суми часткових добутків за алгоритмом Мак-Сорлі (рис.2.27). Частковий добуток у процедурі корекції результату за алгоритмом Мак-Сорлі визначається з використанням звичайного «однорозрядного» алгоритма Бута з урахуванням нульового стану розрядів за межами розрядної сітки множни-ка. Звідси випливає, що цифра Х3 = 1 у наймолодшій парі Х2Х3 множника в процедурі корекції повинна мати вагу
У пристроях множення чисел за груповим, наприклад, двопозиційним алгоритмом Мак-Сорлі у кожному циклі множення чисел виконується аналіз трьох цифр множника, які утворюють поточна пара Х2Х3 і молодша цифра Х1 старшої пари (рис.2.26). При цьому молодша цифра Х3 поточної пари умовно за Мак-Сорлі завжди вважається нулем. Комбінація цифр Х1 Х2 вказаної тріади множника подається кодом Бута2. Молодша цифра Х3 наймолодшої групи Х2Х3 множника використовується для виправлення (корекції) суми часткових добутків за алгоритмом Мак-Сорлі (рис.2.27). Частковий добуток у процедурі корекції результату за алгоритмом Мак-Сорлі визначається з використанням звичайного «однорозрядного» алгоритма Бута з урахуванням нульового стану розрядів за межами розрядної сітки множни-ка. Звідси випливає, що цифра Х3 = 1 у наймолодшій парі Х2Х3 множника в процедурі корекції повинна мати вагу 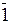 (рис.2.27).
(рис.2.27).
Приклади множення чисел за двопозиційним алгоритмом Мак-Сорлі2 подано на рис.2.28– 2.29.
На завершення можна сказати, що методологічний спосіб, який було застосовано для визначення часткових добутків за двопозиційним груповим алгоритмом Мак-Сорлі2 (рис.2.26 – 2.27), можна застосовувати для визначен-ня часткових добутків за алгоритмом Мак-Сорлі для трирозрядної, чотири-розрядної і будь-якої довжини груп множника.
| Десятковий еквівалент поточної групи (Х1Х2Х3) цифр МК
|
|
|
|
|
|
|
|
|
| Значення поточної групи (Х1Х2Х3) цифр
| 
 0 00 0 00
| 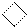
 0 01 0 01
|   0 10
0 10
|   0 11
0 11
| 
 1 00 1 00
|
 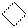 1 01 1 01
|   1 10
1 10
| 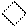
 1 11 1 11
|
| Код Бута поточної пари (Х1Х2) цифр МК (за Х3=0)
| 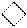 0 00
0 00
|  0 +0
0 +0
|  + -0
+ -0
|  + 00
+ 00
|  - 00
- 00
|  - +0
- +0
|  0 -0
0 -0
|  0 00
0 00
|
  Код Мак-Сорлі (за Х3=0) поточної три-позиційної групи Х1Х2Х3 МК Код Мак-Сорлі (за Х3=0) поточної три-позиційної групи Х1Х2Х3 МК
|  0 00
0 00
|    0 +0
0 +0
|
 0 +0 0 +0
|
   + 00 + 00
| 
 - 00 - 00
| 
 0 -0 0 -0
| 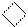  0 -0
0 -0
|
 0 00 0 00
|
| Часткові добутки у поточному циклі за двопозиційним алго-ритмом Мак-Сорлі2
|
(+0)
|
(+2РА)
|
(+2РА)
|
(+4РА)
|
(-4РА)
|
(-2РА)
|
(-2РА)
|
(+0)
|
Рисунок 2.26 – Машинний алгоритм множення чисел за двопозиційним
груповим алгоритмом Мак-Сорлі2 для старшої і внутрішніх пар множника:

 Х2Х3 - поточна пара множника (за алгоритмом Мак-Сорлі умовно вважається, що Х3=0);
Х2Х3 - поточна пара множника (за алгоритмом Мак-Сорлі умовно вважається, що Х3=0);
Х1 - молодша цифра старшої пари множника.
| Десяткові еквіваленти най-молодшої групи (Х1Х2Х3) цифр МК
|
|
|
|
|
|
|
|
|
 Значення наймолодшої групи (Х1Х2Х3) цифр МК Значення наймолодшої групи (Х1Х2Х3) цифр МК
| 
 0 00 0 00
| 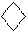  0 01
0 01
| 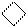  0 10
0 10
|  0 11
0 11
|   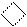 1 00
1 00
|   1 01
1 01
|   1 10
1 10
|  1 11
1 11
|
 Код Бута наймолодшої групи (Х1Х2Х3) цифр МК Код Бута наймолодшої групи (Х1Х2Х3) цифр МК
| 
 0 00 0 00
|  0 +-
0 +-
|
  + -0 + -0
|  
 + 0- + 0-
| 
 - 00 - 00
| 
 - +- - +-
|
 0 -0 0 -0
| 
 0 0- 0 0-
|
| Часткові до-бутки при множенні на
наймолодшу пару (Х2Х3) МК
| За методом Мак-Сорлі2
|
(+0)
|
+2РА
|
+2РА
|
+4РА
|
-4РА
|
-2РА
|
-2РА
|
(+0)
| |
| Корекція до-бутку «Мак-Сорлі2» (за Х3=1)
|
(+0)
| (-РА)
|
(+0)
|
(-РА)
|
(+0)
|
(-РА)
|
(+0)
|
(-РА)
| |
| | | | | | | | | | | | | |
Рисунок 2.27 – Машинний алгоритм множення чисел за двопозиційним алгоритмом Мак-Сорлі2 для наймолодшої пари множника:
 (Х2Х3) – цифрові розряди наймолодшої пари множника;
(Х2Х3) – цифрові розряди наймолодшої пари множника;
Х1 - значення молодшої цифри старшої пари множника;
Х3 – наймолодша цифра множника
| С (АК)
|  РВ РВ
|  РА РА
|
 ± ±
| 9 8765 4321
| ±
| 4 3 2 1
| ±
| 9 8765 4321
| |
0 0 0000 0000,
 1 1 1101 0100, 1 1 1101 0100,
|   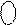 1 0 0 1 1 , 1 0 0 1 1 ,
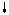 (+4РA) + (-РА)
=(+4РA)
=(-РА) (+4РA) + (-РА)
=(+4РA)
=(-РА)
 2р 2р
  1 1 1 0 0 , 1 1 1 0 0 ,
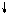 (-4РA)
=(-4РА) (-4РA)
=(-4РА)
| 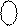 1 1 1111 0101, 1 1 1111 0101,
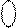  2р
1 1 1101 0100, 2р
1 1 1101 0100,
|
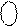 1 1 1101 0100, 1 1 1101 0100,
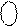 0 0 0000 1011, 0 0 0000 1011,
|
1 1 1101 1111,
0 0 1011 0000,
|
 0 0 1000 1111, 0 0 1000 1111,
|
| | | | | | | | |
Рисунок 2.28 – Приклад множення чисел у доповняльних
кодах за алгоритмом Мак-Сорлі2_Б:
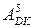 = (-1101)5DK ;
= (-1101)5DK ; 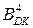 = (-1011) 5DK ;
= (-1011) 5DK ;
(-РА) – корекція суми часткових добутків за алгоритмом Мак-Сорлі (виконується у випадку непарного множника, тобто при РВ(1) =1
 РС (АК) РС (АК)
|  РВ РВ
| РА
|
 ± ±
| 9 8765 4321
| ±
| 4 3 2 1
| ±
| 9 8765 4321
|
0 0 0000 0000,
 0 0 0010 1100, 0 0 0010 1100,
|   1 0 0 1 1 , 1 0 0 1 1 ,
=(-4РA)
 2р 2р
  0 1 1 0 0 , 0 1 1 0 0 ,
(+4РА)+(-РА)
=(+4РА)
=(-РА)
|  1 1 1111 0101, 1 1 1111 0101,
|
 0 0 0010 1100, 0 0 0010 1100,
  2р
0 0 1011 0000,
1 2р
0 0 1011 0000,
1  1 1101 0100, 1 1101 0100,
|
0  0 1000 0100, 0 1000 0100,
0 0 0000 1011,
|
 0 0 1000 1111, 0 0 1000 1111,
|
| | | | | | |
Рисунок 2.29 – Приклад множення чисел у доповняльних
кодах за алгоритмом Мак-Сорлі2_В:
(-РА) – корекція добутку за алгоритмом Мак-Сорлі (виконується
у випадку непарного множника, тобто при РВ(1) = 1)
Вправи та запитання до розділу 2
1. У чому полягає взаємозв’язок між послідовністю цифр множників і розширеним їх поданням у вигляді відповідних поліномів?
2. Визначіть поліноми-співмножників за наступною послідовністю цифр модулів співмножників: МА = 1011; МВ = 1101.
3. Визначіть десятковий еквівалент співмножників МА=1011 і МВ=1101 за допомогою їх поліномів.
4. Для заданих поліномів-співмножників МА і МВ побудуйте їх запис у вигляді послідовності цифр:
МА = a4·23 + a3·22 + a2·21 + a1·20 ;
MB = b4·23 + b3·22 + b2·21 + b1·20.
5. Хай МС(8/1) = МА(4/1)*МВ(4/1),
де MB(4/1) = b4·23 + b3·22 + b2·21 + b1·20.
Доведіть, що добуток МС можна обчислювати за допомогою співвідношень:
МС=2-4[((((0+b1MA)·2-1+ b2MA)·2-1+ b3MA)·2-1+ b4MA)·2-1] ; ( A )
МС=((((0+b1MA)+ b2(MA·2+1))+ b3(MA·2+2))+ b4(MA·2+3)) ; ( Б )
МС=((((0+b4MA) ·2+1+ b3MA) ·2+1+ b2MA)·2+1+ b1MA); ( В )
МС=((((0+b4 (MA·2+3))+ b3(MA·2+2))+ b2(MA·2+1))+ b1(MA·20)). ( Г )
Обчисліть добуток МС і проміжні результати від множення МА=1011 на МВ=1101 за базисними операціями "А", "Б", "В" і "Г". Запропонуйте для базисних операцій "А", "Б", "В" і "Г" прості структури арифметичних пристроїв.
6.  Покажіть, що значення множника В за його доповняльним кодом
Покажіть, що значення множника В за його доповняльним кодом 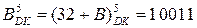 можна знайти за формулою Робертсона:
можна знайти за формулою Робертсона:
В = (-1)·24 + 0·23 + 0·22 + 1·21 + 1·20.
Доведіть, що у загальному випадку поліном множника В із знаком визначається співвідношенням:
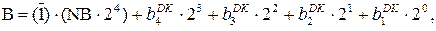
де 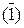 - позначення цифри (-1);
- позначення цифри (-1);
NB – знак доповняльного коду множника В;
 (
( 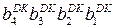 ) – послідовність цифрових розрядів п’ятирозрядного доповняльного коду
) – послідовність цифрових розрядів п’ятирозрядного доповняльного коду 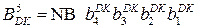 .
.
7. 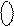 Доведіть, що добуток двох доповняльних кодів
Доведіть, що добуток двох доповняльних кодів 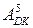 і
і 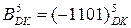 = = 1 0011 можна обчислити за базисною операцією "В" наступним чином:
= = 1 0011 можна обчислити за базисною операцією "В" наступним чином:
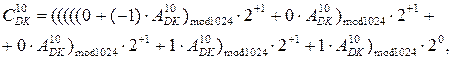
де 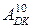 - розширений код
- розширений код 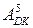 (без зміни його числового значення).
(без зміни його числового значення).
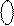
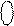 Виконайте вручну операції множення за
Виконайте вручну операції множення за 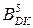 = 1 0011,
= 1 0011,
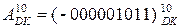 і
і 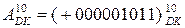 .
.
Знайдіть добуток вказаних вище операндів за базисними операціями "А", "Б", "Г".
8.  Хай множник
Хай множник 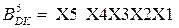 . Покажіть, що за кодом Бута у множнику
. Покажіть, що за кодом Бута у множнику 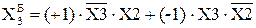 , де
, де 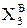 - значення цифри Х3 доповняльного коду
- значення цифри Х3 доповняльного коду 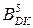 , представленого за кодом Бута.
, представленого за кодом Бута.
Доведіть правило 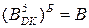 :
:
де 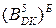 - зображення
- зображення 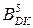 кодом Бута за пятирозрядним форматом;
кодом Бута за пятирозрядним форматом;
В – аргумент доповняльного коду 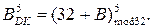
9. 
 Покажіть, що
Покажіть, що 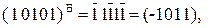
де 1 0101 – зображення числа (-1011) у доповняльному коді.
Знайдіть добуток двох доповняльних кодів 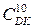 = (
= ( 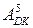 ) * (
) * ( 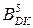 ) при зображенні множника
) при зображенні множника 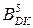 кодом Бута. Вважати, що
кодом Бута. Вважати, що 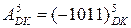 і
і 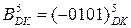 .
.
10. Доведіть, що 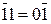 ,
, 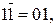
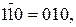
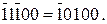
11.  Хай множник
Хай множник 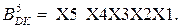 Покажіть, що за кодом Лемана_А у множнику
Покажіть, що за кодом Лемана_А у множнику 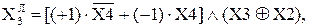 де
де 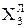 - значення цифри Х3 множника
- значення цифри Х3 множника 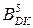 , представленого за Леманом.
, представленого за Леманом.
Знайдіть добуток від множення 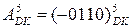 і
і 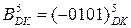 за базисними операціями "А" і "Б" з представленням множника
за базисними операціями "А" і "Б" з представленням множника 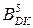 за Леманом.
за Леманом.
12.  Хай множник
Хай множник 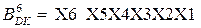 . Покажіть, що за дворозрядним груповим алгоритмом Бута маємо:
. Покажіть, що за дворозрядним груповим алгоритмом Бута маємо:
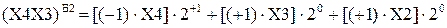 ,
,
де 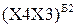 - значення дворозрядної групи (Х4Х3) множника
- значення дворозрядної групи (Х4Х3) множника 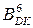 за груповим алгоритмом Бута2_Б.
за груповим алгоритмом Бута2_Б.
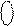 Знайдіть (
Знайдіть ( 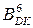 )Б2 = ( 1 00111)Б2.
)Б2 = ( 1 00111)Б2.
Покажіть, що за трирозрядним груповим алгоритмом Бута3_Б маємо:
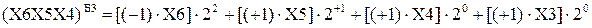 ,
,

 де
де 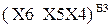 - значення трирозрядної групи (Х6Х5Х4) множника
- значення трирозрядної групи (Х6Х5Х4) множника 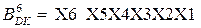 за алгоритмом "Б";
за алгоритмом "Б";
Х3 – старша цифра молодшої групи.
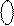 Знайдіть (
Знайдіть ( 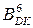 )Б3 = ( 1 011011)Б3.
)Б3 = ( 1 011011)Б3.
13. Знайдіть добуток від множення 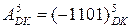 і
і 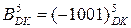 за алгоритмом Бута2 з використанням базисних операцій "А", "Б", "В", "Г".
за алгоритмом Бута2 з використанням базисних операцій "А", "Б", "В", "Г".
14.  Хай множник
Хай множник 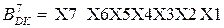 . Покажіть, що за дворозряд-ним груповим алгоритмом Мак-Сорлі маємо:
. Покажіть, що за дворозряд-ним груповим алгоритмом Мак-Сорлі маємо:
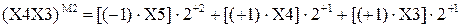 ,
,
де 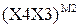 - значення дворозрядної групи множника
- значення дворозрядної групи множника 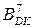 за алгоритмом Мак-Сорлі2;
за алгоритмом Мак-Сорлі2;
Х5 – молодша цифра старшої пари.
Доведіть, що для наймолодшої групи множника справедливо правило:
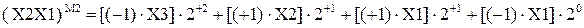 ,
,
де 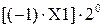 - код корекції (виправлення) значення наймолодшої групи множника за алгоритмом Мак-Сорлі;
- код корекції (виправлення) значення наймолодшої групи множника за алгоритмом Мак-Сорлі;
Х3 – молодша цифра старшої пари.
15. Знайдіть добуток від множення 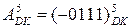 і
і 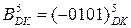 за алгоритмом Мак-Сорлі2 із використанням базисних операцій "А", "Б", "В", "Г".
за алгоритмом Мак-Сорлі2 із використанням базисних операцій "А", "Б", "В", "Г".
3. ТЕОРЕТИЧНІ ЗАСАДИ ТА СТРУКТУРА АРИФМЕТИЧНИХ ПРИСТРОЇВ ДЛЯ ДІЛЕННЯ ЦІЛИХ ЧИСЕЛ
3.1 Теоретичні засади та структура арифметичних пристроїв для ділення цілих чисел у прямих кодах
3.1.1 Теоретичні засади та структура арифметичних пристроїв для ділення подвійного слова на одинарне слово у прямих кодах
Операція ділення цілих чисел, коли у внутрішніх регістрах арифметич-ного пристрою ділене і дільник подаються відповідно в подвоєному і одинар-ному форматах виконується за найпростішими алгоритмами, оскільки в операціях ділення чисел за вказаних форматів практично вилучаються витрати часу на здійснення різного роду попередніх перетворень операндів. У зв’язку з цим саме ця операція ділення цілих чисел застосовується в багатьох сучасних комп’ютерах.
Машинна операція ділення цілих чисел у прямих кодах за зазначених форматів полягає в тому, що за модулем діленого подвійної довжини 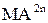 і модулем дільника одинарного формату
і модулем дільника одинарного формату 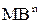 визначаються ціла частина модуля частки
визначаються ціла частина модуля частки 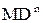 і модуль лишку
і модуль лишку 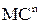 та формується знак прямого коду результату:
та формується знак прямого коду результату:
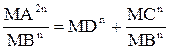 ;
;
ND = NAÅNB; NC = NA, ( 3.1 )
де NA, NB, ND, NC – відповідно знак прямого коду діленого АПК, дільника ВПК, частки DПК і остачі СПК (МСn < МВn).
Згідно з правилами арифметики операція ділення модулів чисел 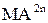 і
і 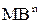 виконується за наступною програмою.
виконується за наступною програмою.
На першому рівні в операції ділення перевіряються логічні умови (повідомні сигнали операційного пристрою) на переривання (блокування) основної частини програми ділення модулів чисел. Для цього, перш за все, проводиться аналіз модуля дільника 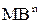 на рівність нулю. У випадку, коли
на рівність нулю. У випадку, коли 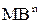 =0, програма ділення аварійно переривається і установлюється ознака переповнення частки
=0, програма ділення аварійно переривається і установлюється ознака переповнення частки 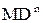 . Тракт блокування операції ділення
. Тракт блокування операції ділення 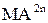 на
на 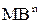 передбачає також аналіз нульового значення чисельника
передбачає також аналіз нульового значення чисельника 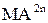 . За умови, коли чисельник
. За умови, коли чисельник 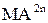 = 0, модулю частки
= 0, модулю частки 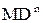 присвоюється нульове значення і операція ділення модулів вважається виконаною. Окрім цих двох випадків блокування операції ділення
присвоюється нульове значення і операція ділення модулів вважається виконаною. Окрім цих двох випадків блокування операції ділення 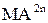 на
на 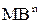 програма ділення пере-ривається з фіксацією переповнення частки
програма ділення пере-ривається з фіксацією переповнення частки 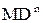 у тому випадку, коли за аргументів
у тому випадку, коли за аргументів 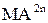 ≠ 0 і
≠ 0 і 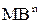 ≠ 0 ціла частина модуля частки MD перевищує гранично-допустимий діапазон представлення результату операції, тобто перевищує n-розрядний (одинарний) формат модуля частки
≠ 0 ціла частина модуля частки MD перевищує гранично-допустимий діапазон представлення результату операції, тобто перевищує n-розрядний (одинарний) формат модуля частки 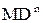 . Розгляне-мо докладно умови, за яких виникає переповнення одинарного формату частки на прикладі виконання операції ділення за наступних форматів:
. Розгляне-мо докладно умови, за яких виникає переповнення одинарного формату частки на прикладі виконання операції ділення за наступних форматів:
MA6 / MB3 ≥ MD3, ( 3.2 )
де МА6 = а6 а5 а4 а3 а2 а1, МВ3= b3b2b1, MD3 = d3d2d1 – відповідно скорочений запис шестирозрядного подвійного діленого і трирозряд-них поліномів дільника і цілої частини частки;
Очевидно, що у загальному випадку кількість значущих цифр цілочислового результату операції ділення (3.2) може змінюватися в межах від одного до шести розрядів, тобто повна частка операції (3.2) визначається шестирозрядним цілочисловим кодом D6, елементами якого є коефіцієнти двійкового полінома d6÷ d1 :
D6 = d6 d5 d4 d3 d2 d1 ( 3.3 )
Отже, результат операції (3.2) у загальному випадку визначається нерівністю:
МА6 / МВ3 ≥ d6×25 + d5×24 + d4×23 + d3×22 + d2×21 + d1×20 , ( 3.4 )
де 25, 24, …, 21, 20 – вага відповідних позицій послідовності цифр повної цілочислової частини частки D6.
Зазначимо, що згідно з (3.1) знаки « = » і « > » у (3.4) визначають операцію ділення відповідно без залишку (МС = 0) і при залишку МС ≠ 0.
Згідно з визначеним машинним алгоритмом (3.2) гранично-допустимий формат цілочислової частини частки операції (3.2) складає три біта. Отже, операція ділення (3.2) можлива без аварійного переповнення модуля частки МD3 у тому випадку, коли старша тріада d6d5d4 повного шестирозрядного полінома частки D6 має нульове значення.
В операції ділення (3.4) старший розряд повної частки d6 = 0у тому випадку, якщо згідно з (3.4) виконується нерівність виду:
МА6 / МВ3 < 1×25,
Таким чином, d6 = 0 за умови:
А6 = МА6 – МВ6 < 0, ( 3.5 )
де А6 – частковий залишок шестирозрядного діленого МА6, який визначає стан старшого коефіцієнта d6 повного полінома частки D6;
МВ6 =МB3 * 25 = b3b2b1 00 000, - формат розширеного модуля дільника МВ3 для визначення стану старшого коефіцієнта d6 повного полінома частки, вага позиції якого дорівнює 25.
За відсутністю значущого розряду у шостому розряді повної частки D6 аналогічним чином можна визначити умову нульового стану коефіцієнта d5 повної частки:
МА6 / МВ3 < 1×24.
Звідси дістанемо:
d5 = 0, якщо А5 = МА6 – МВ5 < 0, ( 3.6 )
де А5 – частковий залишок шестирозрядного діленого МА6 для визначення стану п’ятого розряду d5 у повному поліномі частки D6 за умови, що d6=0;
В5 = МB3 * 24 = b3b2b1 0 000, - стан розширеного модуля дільника для визначення значення коефіцієнта d5 повного полінома частки D6.
24 - ваговий коефіцієнт п’ятої позиції повної частки.
За умови, коли значущі розряди у шостому і п’ятому розрядах повної частки відсутні (d6=0 і d5=0), наступний коефіцієнт повної частки d4 = 0, очевидно, за умови:
МА6 / МВ3 < 1×23,
тобто при виконанні нерівності виду :
А4 = МА6 – МВ4 < 0, ( 3.7 )
де А4 – частковий залишок шестирозрядного діленого МА6, що несе інформацію щодо відсутності значущого розряду у четвертому розряді повної частки D6;
МВ4 = МB3 * 23 = b3b2b1 000, - стан дільника для визначення значення четвертого розряду d4 повної частки D6;
23 – вага четвертої позиції повної частки D6.
У залежностях (3.5) ÷ (3.7), очевидно, справедливі нерівності виду: МВ6 > МВ5 > МВ4, через те, що МВ6 = b3b2b1 00 000, МВ5 = b3b2b1 0 000, МВ4=b3b2b1 000. У зв’язку з цим, якщо частковий залишок А4=МА6– -(b3b2b1 000), утворює від’ємне значення, то часткові залишки А6=МА6– -(b3b2b1 00 000) і А5=МА6–(b3b2b10000) безумовно набувають від’ємні значен-ня. Таким чином, від’ємне значення залишку А4 = МА6 – (b3b2b1)* 23 являє собою необхідну і достатню умову від’ємних значень залишків А6 і А5, тобто визначає умову відсутності значущих цифр в усіх трьох старших розрядах d6 d5 d4 повної частки (3.3) і гарантує відсутність аварійного переповнення гранично-допустимого трирозрядного формату частки. Звідси випливає, що ознака переповнення частки за згаданих форматів результату і аргументів повинна визначатися за співвідношенням:
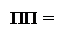
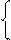 1, якщо
1, якщо 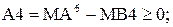 ;
; 
0, якщо 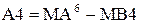 < 0, ( 3.8 )
< 0, ( 3.8 )
де ПП – ознака переповнення трирозрядної частки МD3 (d3d2d1);
МВ4 =МB3 * 23 = b3b2b1 000 – формат розширеного модуля дільника для визначення умови переповнення гранично-допустимого формату цілої частини модуля частки;
А4 - частковий залишок у так званому пробному кроці ділення, який несе інформацію щодо переповнення розрядної сітки цілої частини частки MD3.
У сучасних пристроях для ділення модулів чисел при визначенні часткових залишків операцію віднімання звичайно замінюють додаванням від’ємного дільника в доповняльному коді. У разі застосування допов-няльного коду для визначення пробного залишку діленого А4 залежності (3.8) набувають вигляду:
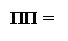
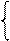 1, якщо NA4 = 0;
1, якщо NA4 = 0; 
0, якщо NA4 = 1, ( 3.9 )
де 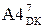 = [ 128 + (МА6 –MB4)]
= [ 128 + (МА6 –MB4)] 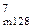 =
=
= [(128 +(+МА6))m128 + (128 + (-MB4)) m128]m128 =
= [(+МА6)  + (- МB4)
+ (- МB4)  )] m128;
)] m128;
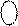 (+МА6)
(+МА6)  = 0 МА6; (- МB)
= 0 МА6; (- МB)  = (128 – MB4) m128 =
= (128 – MB4) m128 =
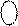
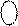
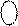 = ((127 – MB4) + 0 000 001) m128 = 1
= ((127 – MB4) + 0 000 001) m128 = 1 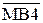 + 0 000 001;
+ 0 000 001;
NA4 – знак доповняльного коду залишку А4.
Типові фрагменти операції ділення для визначення ознаки перепов-нення частки, які реалізують залежності (3.1) і (3.9), подано на рис.3.1 ÷ 3.2.
Рисунок 3.1 - Фрагмент операції ділення чисел А  на В
на В 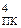 для
для
визначення ознаки переповнення трирозрядної сітки цілої частини
модуля частки МD3 (при ПП = 0)
При відсутності блокування операції ділення чисел за будь-якої із трьох вищеназваних причин в програмі ділення чисел виконується виклик процедури послідовного визначення цифр цілої частини трирозрядної частки МD3, починаючи із старшого розряду d3.
Очевидно, що за згаданих форматів і за умови, коли ціла частина частки МD3 ≤ 111 (за умови, коли ПП = 0), найстарший розряд частки МD3 визначається за співвідношенням:
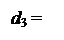
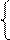 1, якщо МА6 / МB3 ≥ 22,
1, якщо МА6 / МB3 ≥ 22,
0, якщо МА6 / МB3 < 22.
Із цього випливає, що найстарший розряд частки d3 потрібно обчислювати за нерівностями виду:
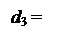
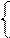 1, якщо А3 = МА6 - МB3 ≥ 0,
1, якщо А3 = МА6 - МB3 ≥ 0,
0, якщо А3 = МА6 - МB3 < 0, ( 3.10)
де МВ3 = (МB3*22) = (МB300) = (b3b2b1 00) – розширений код модуля дільника для визначення позиції d3 частки із ваговим коефіцієнтом 22;
А3 – частковий залишок діленого МА6 для визначення стану найстаршого коефіцієнта d3 полінома частки МD3 = d3d2d1.
Рисунок 3.2 - Фрагмент операції ділення чисел А  на В
на В 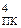 для
для
визначення ознаки переповнення трирозрядної сітки цілої частини
частки МD3 ( при ПП = 1)
У зв’язку з тим, що МВ4 = МB3 000, очевидно, розширений формат модуля дільника МВ3 взаємопов’язаний із кодом МВ4 співвідношенням: МВ3 = МВ4 / 2, ( 3.11 )
де МВ4 – розширений формат модуля дільника в пробному кроці операції ділення.
У разі застосування доповняльного коду для визначення залишку А3 залежності (3.10) набувають вигляду:
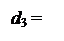
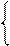 1, якщо NA3 = 0;
1, якщо NA3 = 0;  0, якщо NA3 = 1, ( 3.12 )
0, якщо NA3 = 1, ( 3.12 )
де 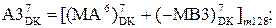 ( 3.13 )
( 3.13 )
МА6 – первинне значення модуля діленого;
Оскільки згідно з (3.9) при відсутності переповнення частки (за ПП=0) у пробному циклі формується від’ємна остача A4, для обчислення залишку 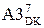 за формулою (3.13) в пристрої ділення спочатку необхідно відновити первинний стан модуля діленого МА6, тобто згідно з (3.9) виконати операцію:
за формулою (3.13) в пристрої ділення спочатку необхідно відновити первинний стан модуля діленого МА6, тобто згідно з (3.9) виконати операцію:
МА6 = [(А4) 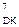 + (+МВ4)
+ (+МВ4) 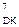 ]m128 ( 3.14 )
]m128 ( 3.14 )
Таким чином, згідно з (3.13) і (3.14) для визначення найстаршої позиції d3 модуля частки потрібно виконати таку послідовность операцій:
1. МА6 = [(А4) 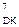 + (+МВ4)
+ (+МВ4) 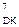 ]m128; ( 3.15 )
]m128; ( 3.15 )
2. (А3) 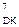 = [(МА6)
= [(МА6) 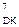 + ((-МВ4)/2)
+ ((-МВ4)/2) 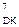 ]m128; ( 3.16 )
]m128; ( 3.16 )
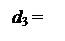
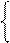 3. 1, якщо NA3 = 0;
3. 1, якщо NA3 = 0; 
0, якщо NA3 = 1. ( 3.17 )
Аналогічним чином можна визначити залежності для обчислення наступних позицій d2 і d1 частки.
Спочатку розглянемо алгоритм визначення цифри d2 частки за умови, коли попередня цифра частки d3 = 1, тобто за А3 ≥ 0.
Якщо d3 = 1, то згідно з (3.4) маємо:
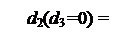
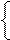 1, якщо МА6 / МB3 ≥ (22 + 21);
1, якщо МА6 / МB3 ≥ (22 + 21);
0, якщо МА6 / МB3 < (22 + 21),
де 22, 21 – вага коефіцієнтів d3 і d2 полінома частки МD3 = d3d2d1.
Із цього виразу випливають нерівності виду:
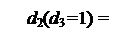
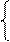 1, якщо МА6 - МB3 – МB2 ≥ 0;
1, якщо МА6 - МB3 – МB2 ≥ 0;
0, якщо МА6 - МB3 – МB2 < 0,
де МB3 = МB3·(22) = МB3 00; МB2 = МB3·(21) = МB3 0.
Звідси дістанемо:
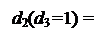
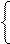 1, якщо A2 ≥ 0;
1, якщо A2 ≥ 0;
0, якщо A2 < 1,
де А2 = (А3 – MВ2); В2 = (MВ3) /2;
MВ2, MВ3 – стан первинного дільника MВ3 = b3b2b1 відповідно у поточному і попередньому циклах ділення;
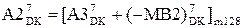 ;
;
А3 – залишок діленого у попередньому циклі ділення (за умови, коли d3= 1 і А3 ≥ 0 ).
Таким чином, за умови, коли d3 = 1 (за А3 ≥ 0), наступну цифру d2 частки потрібно обчислювати за співвідношеннями:
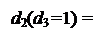
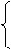 1, якщо NA2 = 0;
1, якщо NA2 = 0;
0, якщо NA2 = 1, ( 3.18 )
де 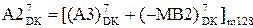 ;
;
MВ2 = (MВ3)/2 - стан дільника для визначення позиції d2 частки.
Якщо коефіцієнт d3 розшукованого полінома частки (d3 d2 d1) дорівнює нулю (d3 = 0), то позицію d2 частки згідно з (3.4) потрібно обчислювати за нерівностями виду:
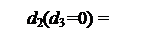
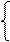 1, якщо МА6 / МB3 ≥ 21;
1, якщо МА6 / МB3 ≥ 21;
0, якщо МА6 / МB3 < 21,
де ( 21) – вага позиції d2 частки.
Звідси дістанемо:
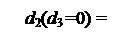
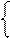 1, якщо А2 = МА6 – МB2 ≥ 0;
1, якщо А2 = МА6 – МB2 ≥ 0;
0, якщо А2 = МА6 – МB2 < 0. ( 3.19 )
За умови, коли d3 = 0, попередній залишок діленого А3 < 0, тому для обчислення поточної цифри частки d2 за нерівностями (3.19) спочатку необхідно відновити модуль діленого МА6. Згідно з (3.10) для цього потрібно виконати операцію:
МА6 = [A3+ (+МВ3 )] ( 3.20 )
Якщо від’ємний залишок А3 визначений у доповняльному коді, то відновлення залишку, очевидно, потрібно здійснювати за правилами підсумовування доповняльних кодів:
МА6 = [ 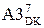 + (+МВ3 )
+ (+МВ3 ) 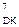 ]m128. ( 3.21 )
]m128. ( 3.21 )
Узагальнюючи (3.18) ÷(3.20), для визначення коефіцієнтів полінома частки МD3 = d3d2d1 маємо наступну послідовність операцій:
MB3 = (MB4)/2;
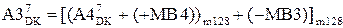 ; ( 3.22 )
; ( 3.22 )
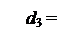
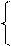 1, якщо NA3 = 0;
1, якщо NA3 = 0; 
0, якщо NA3 = 1; ( 3.23 )
MB2 = (MB3)/2;
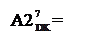
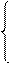
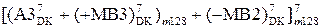 ,
,
якщо NА3 = 1;
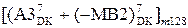 , якщо NА3 = 0; ( 3.24 )
, якщо NА3 = 0; ( 3.24 )
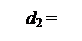
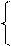 1, якщо NA2 = 0;
1, якщо NA2 = 0; 
0, якщо NA2 = 1; ( 3.25 )
MB1 = (MB2)/2;
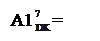
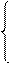
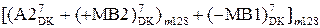 ,
,
якщо NА2 = 1;
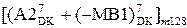 , якщо NА2 = 0; ( 3.26 )
, якщо NА2 = 0; ( 3.26 )
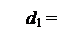
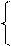 1, якщо NA1 = 0;
1, якщо NA1 = 0; 
0, якщо NA1 = 1; ( 3.27 )
де А4 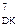 - частковий залишок подвійного формату діленого у пробному кроці операції ділення, який несе інформацію щодо переповнення розрядної сітки цілої частини частки;
- частковий залишок подвійного формату діленого у пробному кроці операції ділення, який несе інформацію щодо переповнення розрядної сітки цілої частини частки;
і = 3,2,1 – номери позицій цілої частини частки;
МВ4 = b3b2b1 000 – стан розширеного подвійного формату модуля дільника у пробному циклі операції ділення.
Модуль остачі МС6 згідно з (3.1) пов'язаний з аргументами операції ділення співвідношенням:
МА6 = (МВ3)*(МD3) +MC6.
У розгорнутій формі маємо:
MC6 = МА6 - МВ3(d3·22 + d2·21 + d1·20).
Звідси дістанемо:
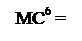
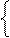 МА6 - МВ3(d3·22 + d2·21 +20), якщо d1 = 1,
МА6 - МВ3(d3·22 + d2·21 +20), якщо d1 = 1,
МА6 - МВ3(d3·22 + d2·21), якщо d1 = 0.
Згідно з (3.24) в останньому циклі ділення частковий залишок А1 обчислюється за формулою:
А1 = МА6 - (МВ3·22)d3 – (МВ3·21)d2 + 1 =
= МА6 - (МВ3·22)d3 – (МВ3·21)d2 – МВ3.
Звідси випливає, що останній залишок діленого А1 взаємопов’язаний з остачею МС6 співвідношенням:
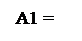
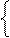 МС6, якщо d1 = 1, тобто А1 ≥ 0;
МС6, якщо d1 = 1, тобто А1 ≥ 0;
МС6 - МВ3, якщо d1 = 0, тобто А1< 0.
Таким чином, маємо:
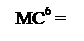
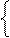 А1, якщо NA1 = 0;
А1, якщо NA1 = 0;
А1 + (+МВ3), якщо NA1 = 1.
Звідси дістанемо:
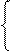
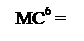 (А1
(А1 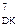 )6, якщо NA1 ≥ 0;
)6, якщо NA1 ≥ 0;
[(А1 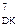 + (+МВ3)
+ (+МВ3) 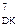 )m128]6, якщо NA1 < 0.
)m128]6, якщо NA1 < 0.
Схема блока ділення чисел, представлених у прямому коді, за розгляну-тим алгоритмом зі зсувом вправо модуля дільника МВ (за алгоритмом «б») і відновленням залишку (ЗВЗ) подана на рис.3.3.
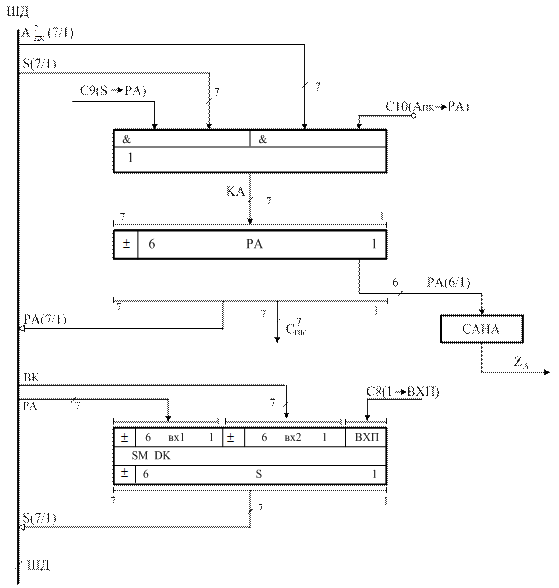
Рисунок 3.3,а – Cхема регістра діленого (РА) і суматора ( SM)
блока ділення за алгоритмом «б» з відновленням залишку (ЗВЗ)
Схема блока ділення містить:
- регістр А для приймання прямого коду діленого (А  ) або рядку цифр на виході суматора SM;
) або рядку цифр на виході суматора SM;
- регістр В для приймання прямого коду дільника (В 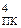 ) та формування його подвійного формату на відповідних входах суматора SM;
) та формування його подвійного формату на відповідних входах суматора SM;
- лічильник циклів СТ;
- комутатор КА для формування змінних на інформаційних входах регістра А;
- комутатор ВК для подання прямого або оберненого коду дільника на входи суматора SM;
- тригер ознаки переповнення (ТПП) цілої частини частки;
- схему аналізу нульового стану модулів регістра А (САНА) і регістра В (CAHB).
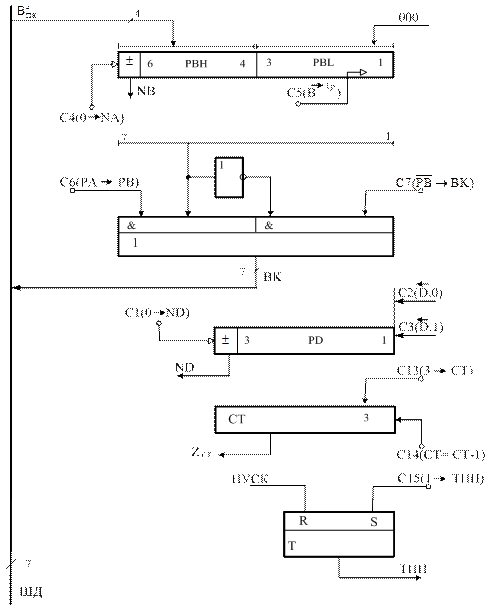
Рисунок 3.3,б – Схема регістра дільника (РВ), частки (PD),
лічильника циклів (СТ) та тригера переповнення (ТПП) блока
ділення за алгоритмом «б» з відновленням залишку (ЗВЗ)
Мікропрограма роботи блока ділення чисел подана на рис.3.4. На першому рівні мікропрограми за сигналом «Пуск» перевіряється нульове значення дільника (стан логічного сигналу ZB) і, якщо ZB = 1 (тобто за МВ3=000), керуючий автомат встановлює у стан «1» тригер ТПП (тригер переповнення) і програма ділення аварійно переривається шляхом переходу керуючого автомата у стан






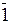 (рис.2.27).
(рис.2.27).
 0 00
0 00
 0 01
0 01

 0 10
0 10

 0 11
0 11

 1 00
1 00

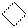 1 01
1 01

 1 10
1 10
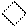
 1 11
1 11
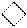 0 00
0 00
 0 +0
0 +0
 0 -0
0 -0

 Код Мак-Сорлі (за Х3=0) поточної три-позиційної групи Х1Х2Х3 МК
Код Мак-Сорлі (за Х3=0) поточної три-позиційної групи Х1Х2Х3 МК
 0 00
0 00

 0 +0
0 +0
 + 00
+ 00


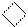

 Х2Х3 - поточна пара множника (за алгоритмом Мак-Сорлі умовно вважається, що Х3=0);
Х2Х3 - поточна пара множника (за алгоритмом Мак-Сорлі умовно вважається, що Х3=0); Значення наймолодшої групи (Х1Х2Х3) цифр МК
Значення наймолодшої групи (Х1Х2Х3) цифр МК

 0 00
0 00
 0 01
0 01
 0 10
0 10
 0 11
0 11

 1 00
1 00
 1 01
1 01
 1 10
1 10
 1 11
1 11


 + 0-
+ 0-

 0 -0
0 -0

 (Х2Х3) – цифрові розряди наймолодшої пари множника;
(Х2Х3) – цифрові розряди наймолодшої пари множника; РВ
РВ
 РА
РА
 ±
±
 1 1 1101 0100,
1 1 1101 0100,


 1 0 0 1 1 ,
1 0 0 1 1 ,
 (+4РA) + (-РА)
=(+4РA)
=(-РА)
(+4РA) + (-РА)
=(+4РA)
=(-РА)
 2р
2р

 1 1 1 0 0 ,
1 1 1 0 0 ,
 (-4РA)
=(-4РА)
(-4РA)
=(-4РА)
 1 1 1111 0101,
1 1 1111 0101,
 2р
1 1 1101 0100,
2р
1 1 1101 0100,
 1 1 1101 0100,
1 1 1101 0100,
 0 0 1000 1111,
0 0 1000 1111,
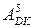 = (-1101)5DK ;
= (-1101)5DK ; 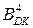 = (-1011) 5DK ;
= (-1011) 5DK ; РС (АК)
РС (АК)
 РВ
РВ

 2р
2р
 0 1 1 0 0 ,
0 1 1 0 0 ,
 1 1 1111 0101,
1 1 1111 0101,
 0 1000 0100,
0 1000 0100,
 0 0 1000 1111,
0 0 1000 1111,
 Покажіть, що значення множника В за його доповняльним кодом
Покажіть, що значення множника В за його доповняльним кодом 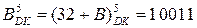 можна знайти за формулою Робертсона:
можна знайти за формулою Робертсона: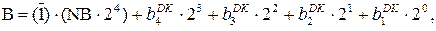
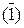 - позначення цифри (-1);
- позначення цифри (-1); (
( 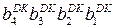 ) – послідовність цифрових розрядів п’ятирозрядного доповняльного коду
) – послідовність цифрових розрядів п’ятирозрядного доповняльного коду 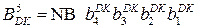 .
.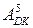 і
і 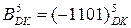 = = 1 0011 можна обчислити за базисною операцією "В" наступним чином:
= = 1 0011 можна обчислити за базисною операцією "В" наступним чином: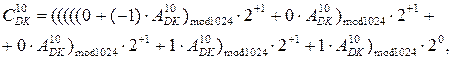
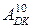 - розширений код
- розширений код 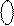
 Виконайте вручну операції множення за
Виконайте вручну операції множення за 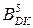 = 1 0011,
= 1 0011,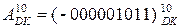 і
і 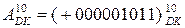 .
. Хай множник
Хай множник 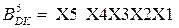 . Покажіть, що за кодом Бута у множнику
. Покажіть, що за кодом Бута у множнику 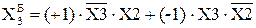 , де
, де 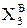 - значення цифри Х3 доповняльного коду
- значення цифри Х3 доповняльного коду 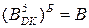 :
: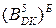 - зображення
- зображення 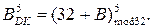
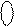
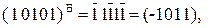
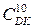 = (
= ( 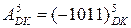 і
і 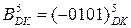 .
.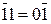 ,
, 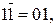
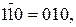
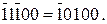
 Хай множник
Хай множник 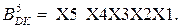 Покажіть, що за кодом Лемана_А у множнику
Покажіть, що за кодом Лемана_А у множнику 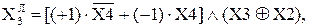 де
де 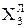 - значення цифри Х3 множника
- значення цифри Х3 множника 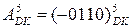 і
і  Хай множник
Хай множник 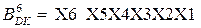 . Покажіть, що за дворозрядним груповим алгоритмом Бута маємо:
. Покажіть, що за дворозрядним груповим алгоритмом Бута маємо: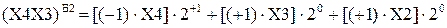 ,
,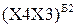 - значення дворозрядної групи (Х4Х3) множника
- значення дворозрядної групи (Х4Х3) множника 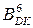 за груповим алгоритмом Бута2_Б.
за груповим алгоритмом Бута2_Б.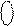 Знайдіть (
Знайдіть ( 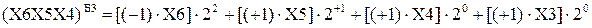 ,
,
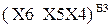 - значення трирозрядної групи (Х6Х5Х4) множника
- значення трирозрядної групи (Х6Х5Х4) множника 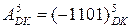 і
і 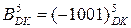 за алгоритмом Бута2 з використанням базисних операцій "А", "Б", "В", "Г".
за алгоритмом Бута2 з використанням базисних операцій "А", "Б", "В", "Г".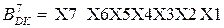 . Покажіть, що за дворозряд-ним груповим алгоритмом Мак-Сорлі маємо:
. Покажіть, що за дворозряд-ним груповим алгоритмом Мак-Сорлі маємо: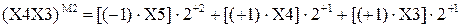 ,
,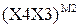 - значення дворозрядної групи множника
- значення дворозрядної групи множника 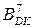 за алгоритмом Мак-Сорлі2;
за алгоритмом Мак-Сорлі2;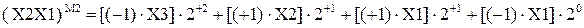 ,
,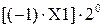 - код корекції (виправлення) значення наймолодшої групи множника за алгоритмом Мак-Сорлі;
- код корекції (виправлення) значення наймолодшої групи множника за алгоритмом Мак-Сорлі;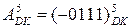 і
і 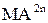 і модулем дільника одинарного формату
і модулем дільника одинарного формату 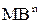 визначаються ціла частина модуля частки
визначаються ціла частина модуля частки 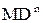 і модуль лишку
і модуль лишку 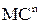 та формується знак прямого коду результату:
та формується знак прямого коду результату: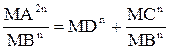 ;
;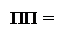
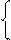 1, якщо
1, якщо 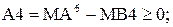 ;
; 
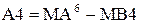 < 0, ( 3.8 )
< 0, ( 3.8 )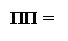
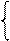 1, якщо NA4 = 0;
1, якщо NA4 = 0; 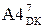 = [ 128 + (МА6 –MB4)]
= [ 128 + (МА6 –MB4)] 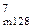 =
= + (- МB4)
+ (- МB4) 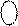 (+МА6)
(+МА6) 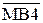 + 0 000 001;
+ 0 000 001; ( ± МD3)ПК
( ± МD3)ПК
 ( ± МА6)ПК
( ± МА6)ПК
 ± 3 2 1
± 3 2 1
 Х ХХХ
Х ХХХ
 D
D
 Х ХХ ±
NA4 = 1
(A4 < 0),
тому ПП = 0
Х ХХ ±
NA4 = 1
(A4 < 0),
тому ПП = 0



 ± 0 1 1 0 0 1
± 0 1 1 0 0 1
 NA NB
ND
NA NB
ND
 0 0 1 1 0 0 1
1 0 1 1 0 0 0
0 0 1 1 0 0 1
1 0 1 1 0 0 0

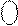 1 1 0 0 0 0 1
1 1 0 0 0 0 1
 NA4=1
NA4=1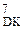 = (+МА6)
= (+МА6)  на В
на В 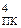 для
для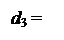
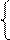 1, якщо МА6 / МB3 ≥ 22,
1, якщо МА6 / МB3 ≥ 22,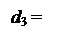
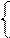 1, якщо А3 = МА6 - МB3 ≥ 0,
1, якщо А3 = МА6 - МB3 ≥ 0,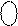 ( ± МD3)ПК
( ± МD3)ПК
 Х ХХХ
Х ХХХ
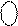 ± 1 1 0 0 0 1
± 1 1 0 0 0 1
 NA NB
ND
NA NB
ND

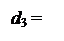
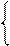 1, якщо NA3 = 0;
1, якщо NA3 = 0; 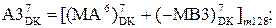 ( 3.13 )
( 3.13 )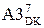 за формулою (3.13) в пристрої ділення спочатку необхідно відновити первинний стан модуля діленого МА6, тобто згідно з (3.9) виконати операцію:
за формулою (3.13) в пристрої ділення спочатку необхідно відновити первинний стан модуля діленого МА6, тобто згідно з (3.9) виконати операцію: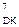 + (+МВ4)
+ (+МВ4) 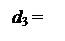
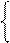 3. 1, якщо NA3 = 0;
3. 1, якщо NA3 = 0; 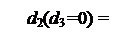
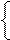 1, якщо МА6 / МB3 ≥ (22 + 21);
1, якщо МА6 / МB3 ≥ (22 + 21);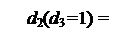
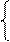 1, якщо МА6 - МB3 – МB2 ≥ 0;
1, якщо МА6 - МB3 – МB2 ≥ 0;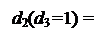
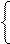 1, якщо A2 ≥ 0;
1, якщо A2 ≥ 0;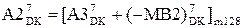 ;
;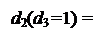
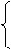 1, якщо NA2 = 0;
1, якщо NA2 = 0;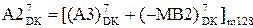 ;
;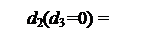
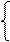 1, якщо МА6 / МB3 ≥ 21;
1, якщо МА6 / МB3 ≥ 21;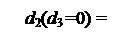
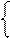 1, якщо А2 = МА6 – МB2 ≥ 0;
1, якщо А2 = МА6 – МB2 ≥ 0;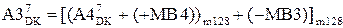 ; ( 3.22 )
; ( 3.22 )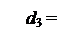
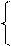 1, якщо NA3 = 0;
1, якщо NA3 = 0; 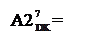
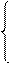
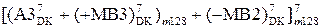 ,
,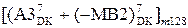 , якщо NА3 = 0; ( 3.24 )
, якщо NА3 = 0; ( 3.24 )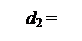
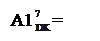
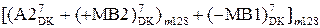 ,
,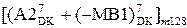 , якщо NА2 = 0; ( 3.26 )
, якщо NА2 = 0; ( 3.26 )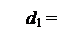
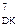 - частковий залишок подвійного формату діленого у пробному кроці операції ділення, який несе інформацію щодо переповнення розрядної сітки цілої частини частки;
- частковий залишок подвійного формату діленого у пробному кроці операції ділення, який несе інформацію щодо переповнення розрядної сітки цілої частини частки;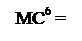
 МА6 - МВ3(d3·22 + d2·21 +20), якщо d1 = 1,
МА6 - МВ3(d3·22 + d2·21 +20), якщо d1 = 1,