У пристроях множення за груповим, наприклад, двопозиційним методом Бута значення окремих цифр у групі спочатку визначається за звичайним кодом Бута, а потiм сполучення виду 1 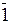 [1×21+(-1)×20] заміщаються рівнозначною комбінацією 01[0×21+1×20], а сполученя виду
[1×21+(-1)×20] заміщаються рівнозначною комбінацією 01[0×21+1×20], а сполученя виду 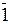 1[(-1)×21+1×20] - рівнозначною комбінацією 0
1[(-1)×21+1×20] - рівнозначною комбінацією 0 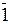 [0×21+(-1)×20].
[0×21+(-1)×20].
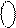
 У разі, коли, наприклад, В= -01011 і
У разі, коли, наприклад, В= -01011 і 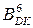 = 1 10101 та (
= 1 10101 та ( 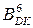 )6БУТА =
)6БУТА =  , то зображення множника за груповим двопозиційним кодом Бута (Бута2) має вигляд (рис.2.20):
, то зображення множника за груповим двопозиційним кодом Бута (Бута2) має вигляд (рис.2.20):

 (
( 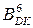 )6БУТА2 =
)6БУТА2 = 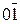 01 01 .
01 01 .




 Iз цих мiркувань випливає, що для визначення часткових добутків у пристої множення чисел за методом Бута2 необхiдно виконувати аналіз трьох цифр множника, які утворюють поточна пара множника Х1Х2 і старша цифра Х3 молодшої пари Х3Х4 , тобто комбінації цифр: Х1Х2Х3 .
Iз цих мiркувань випливає, що для визначення часткових добутків у пристої множення чисел за методом Бута2 необхiдно виконувати аналіз трьох цифр множника, які утворюють поточна пара множника Х1Х2 і старша цифра Х3 молодшої пари Х3Х4 , тобто комбінації цифр: Х1Х2Х3 .
У разі застосування алгоритмів «А» і «Б» (рис.2.21) за методом Бута2 у кожному циклі аналізується найменша пара регістра множника [РВ(2) РВ(1)] і додатковий розряд множника РВ(0), в якому до початку множення встановлюється нульовий стан, тобто нульове значення старшої цифри молодшої пари, яка розмiщується за межами регістра множника. У процесі роботи пристрою після кожного арифметичного зсуву регістра множника на два біта в бік молодших розрядів у додатковий розряд множника РВ(0) записується старша цифра попередньої пари розрядів, тобто РВ(2).
| Десятковий еквівалент по-точної трипозиційної групи (Х1Х2Х3) цифр множника (МК)
|
|
|
|
|
|
|
|
|
| Поточна трипозиційна група (Х1Х2Х3) цифр (МК)
| 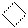  00 0
00 0
| 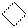  00 1
00 1
| 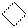  01 0
01 0
| 
 01 1 01 1
|   10 0
10 0
| 
 10 1 10 1
|   11 0
11 0
|   11 1
11 1
|
  Код Бута – пари Х1Х2 три-позиційної групи (Х1Х2Х3) МК Код Бута – пари Х1Х2 три-позиційної групи (Х1Х2Х3) МК
| 
|  0+
0+
|  +-
+-
|  +0
+0
|  -0
-0
|
 -+ -+
|  0-
0-
| 
|
| Код Бута2 пари Х1Х2 трипозиційної групи (Х1Х2Х3) МК
|
 00 00
|  0+
0+
|
 0+ 0+
|  +0
+0
|  -0
-0
|  0-
0-
|  0-
0-
| 
|
| Часткові добутки у по-точному циклі за алгоритмом Бута2
|
(+0)
|
(+РА)
|
(+РА)
|
(+2РА)
|
(-2РА)
|
(-РА)
|
(-РА)
|
(+0)
| |
| | | | | | | | | | | | |
Примітка: РА – регістр множеного
Рисунок 2.20 – Машинний алгоритм множення чисел
за двопозиційним груповим алгоритом Бута2

Рисунок 2.21 – Схема аналізатора поточної групи множника
[РВ(2) РВ(1) РВ(0)] за груповими алгоритмами Бута2_А та Бута2_Б
У пристроях множення чисел за алгоритмами «В» і «Г» з прискоренням операції множення за алгоритмом Бута2 (рис.2.20) у кожному циклі для визначення часткових добутків аналізуються три старші позиції розширеного у бік старших розрядів регістра множника [РВ(6) РВ(5) РВ(4)], тобто поточна пара [РВ(6) РВ(5)] і старша цифра РВ(4) молодшої пари [РВ(4) РВ(3)] (рис.2.22). У кожному циклі роботи пристрою при логічному зсуві регістра множника на два біта у бік старших розрядів поточна пара розрядів заміщується черговою парою розрядів множника. Зазначимо, що у першому кроці операції множення поточну пару складають знакові розряди розширеного формату множника (рис.2.22).
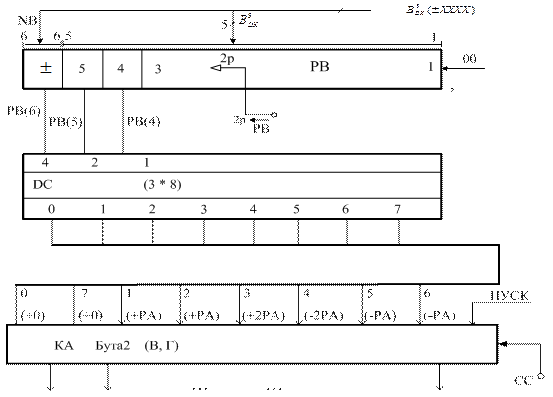
Рисунок 2.22 – Схема аналізатора поточної групи множника
[РВ(6) РВ(5) РВ(4)] за груповими алгоритмами Бута2_В та Бута2_Г
Приклади множення чисел у доповняльних кодах за алгоритмом Бута2 наведено на рис.2.23 – 2.24.
У випадку, коли за груповим методом Бута у кожному циклі множення виконується на три цифри множника, часткові добутки формуються також шляхом мінімізації кількості значущих цифр у звичайному коді Бута (рис.2.25). Проте, схема формувача часткових добутків і алгоритм роботи блока множення у цьому випадку значно ускладнюється порівняно із схемою множення за алгоритмом Бута2.
На завершення можна сказати, що методологічний спосіб, який було застосовано для визначення часткових добутків за алгоритмами Бута2 (рис.2.20) і Бута3 (рис.2.25), можна також застосувати для визначення часткових добутків для чотирирозрядної, п’ятирозрядної і будь-якої довжини групи множника.
Рисунок 2.23 – Приклад множення чисел у доповняльних
кодах за груповим алгоритмом Бута2_Б
Рисунок 2.24 – Приклад множення чисел у доповняльних
кодах за груповим алгоритмом Бута2_В
| Десятковий еквівалент поточної групи (Х1Х2Х3Х4) цифр МК
|
|
|
|
|
| Значення поточної групи (Х1Х2Х3Х4) цифр МК
|   000 0
000 0
|   000 1
000 1
|   001 0
001 0
|
  001 1 001 1
|
 Код Бута поточної три-позиційної групи Х1Х2Х3 МК Код Бута поточної три-позиційної групи Х1Х2Х3 МК
| 
|  00+
00+
|  0+-
0+-
|  0+0
0+0
|
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
| 
|  00+
00+
|  00+
00+
|  0+0
0+0
|
| Часткові добутки у поточному циклі за методом Бута3
|
(+0)
|
(+РА)
|
(+РА)
|
(+2РА)
|
Рисунок 2.25,а – Блок 1 множення чисел за
трипозиційним груповим алгоритмом Бута3
| Десятковий еквівалент поточної групи (Х1Х2Х3Х4) цифр МК
|
|
|
|
|
| Значення поточної групи (Х1Х2Х3Х4) цифр МК
|   010 0
010 0
|   010 1
010 1
|
  011 0 011 0
|   011 1
011 1
|
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК Код Бута поточної трипозиційної групи Х1Х2Х3 МК
|  +-0
+-0
|  +-+
+-+
|  +0-
+0-
|  +00
+00
|
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
|  0+0
0+0
|  +0-
+0-
|  +0-
+0-
|  +00
+00
|
| Часткові добутки у поточному циклі за методом Бута3
| (+2РА)
| (+4РА)+
(-РА)
| (+4РА)+
(-РА)
| (+4РА)
|
Рисунок 2.25,б - Блок 2 множення чисел за
трипозиційним груповим алгоритмом Бута3
| Десятковий еквівалент поточної групи (Х1Х2Х3Х4) цифр МК
|
|
|
|
|
| Значення поточної групи (Х1Х2Х3Х4) цифр МК
|   100 0
100 0
|   100 1
100 1
|
  101 0 101 0
| 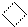  101 1
101 1
|
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК Код Бута поточної трипозиційної групи Х1Х2Х3 МК
|  -00
-00
|  -0+
-0+
|  -+-
-+-
|  -+0
-+0
|
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
|  -00
-00
|  -0+
-0+
|  -0+
-0+
|  0-0
0-0
|
| Часткові добутки у поточному циклі за методом Бута3
| (-4РА)
| (-4РА)+
(РА)
| (-4РА)+
(РА)
|
(-2РА)
|
Рисунок 2.25,в - Блок 3 множення чисел за
трипозиційним груповим алгоритмом Бута3
| Десятковий еквівалент поточної групи (Х1Х2Х3Х4) цифр МК
|
|
|
|
|
| Значення поточної групи (Х1Х2Х3Х4) цифр МК
|   110 0
110 0
|   110 1
110 1
|
 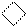 111 0 111 0
| 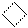  111 1
111 1
|
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК Код Бута поточної трипозиційної групи Х1Х2Х3 МК
|  0-0
0-0
|  0-+
0-+
|  00-
00-
| 
|
 Код Бута3 поточної трипозиційної групи Х1Х2Х3 МК Код Бута3 поточної трипозиційної групи Х1Х2Х3 МК
|  0-0
0-0
|  00-
00-
|  00-
00-
| 
|
| Часткові добутки у поточному циклі за методом Бута3
|
(-2РА)
|
(-РА)
|
(-РА)
|
(+0)
|
Рисунок 2.25,г - Блок 4 множення чисел за
трипозиційним груповим алгоритмом Бута3


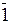 [1×21+(-1)×20] заміщаються рівнозначною комбінацією 01[0×21+1×20], а сполученя виду
[1×21+(-1)×20] заміщаються рівнозначною комбінацією 01[0×21+1×20], а сполученя виду 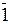 1[(-1)×21+1×20] - рівнозначною комбінацією 0
1[(-1)×21+1×20] - рівнозначною комбінацією 0 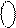
 У разі, коли, наприклад, В= -01011 і
У разі, коли, наприклад, В= -01011 і 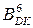 = 1 10101 та (
= 1 10101 та ( 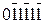 , то зображення множника за груповим двопозиційним кодом Бута (Бута2) має вигляд (рис.2.20):
, то зображення множника за груповим двопозиційним кодом Бута (Бута2) має вигляд (рис.2.20):
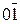 01 01 .
01 01 .



 00 0
00 0
 00 1
00 1
 01 1
01 1
 10 0
10 0
 10 1
10 1

 11 1
11 1

 Код Бута – пари Х1Х2 три-позиційної групи (Х1Х2Х3) МК
Код Бута – пари Х1Х2 три-позиційної групи (Х1Х2Х3) МК
 +0
+0
 -0
-0
 -+
-+

 00
00
 0+
0+
 0+
0+


 РС (АК)
РС (АК)
 РВ 2р
РВ 2р
 2р РА
2р РА
 ±
±

 1 0 1 1 0
1 0 1 1 0
 0 - ,
(-РА)
0 - ,
(-РА)
 = (- РA) 2р
= (- РA) 2р

 - + ,
- + , 1 1 111 001,
1 1 111 001,
 2р
2р
 1 1 100 100,
1 1 100 100,
 0 0 000 111,
+
0 0 000 111,
+
 0 0 011 100,
0 0 011 100,
 0 0 100 011,
0 0 100 011,
 0 0 000 111,
0 0 000 111,

 1 0 1 1,
1 0 1 1,
 - +
(-РА)
=(- РA)
- +
(-РА)
=(- РA)
 2р
2р

 1 1 ,0 0
1 1 ,0 0
 - +
(-РА)
= (-РА)
- +
(-РА)
= (-РА)

 2р
0 0 011 100,
+
2р
0 0 011 100,
+
 0 0 100 011,
0 0 100 011,

 000 0
000 0



 001 1
001 1
 Код Бута поточної три-позиційної групи Х1Х2Х3 МК
Код Бута поточної три-позиційної групи Х1Х2Х3 МК

 00+
00+
 0+-
0+-
 0+0
0+0
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК

 00+
00+
 00+
00+
 0+0
0+0

 010 1
010 1

 011 0
011 0
 011 1
011 1
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК
Код Бута поточної трипозиційної групи Х1Х2Х3 МК
 +-+
+-+
 +0-
+0-
 +00
+00
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
 +0-
+0-

 100 0
100 0
 101 0
101 0
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК
Код Бута поточної трипозиційної групи Х1Х2Х3 МК
 -+0
-+0
 Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
Код Бута3 поточної три-позиційної групи Х1Х2Х3 МК
 -00
-00
 -0+
-0+
 Код Бута поточної трипозиційної групи Х1Х2Х3 МК
Код Бута поточної трипозиційної групи Х1Х2Х3 МК
 00-
00-
 Код Бута3 поточної трипозиційної групи Х1Х2Х3 МК
Код Бута3 поточної трипозиційної групи Х1Х2Х3 МК
 0-0
0-0