Множення чисел iз молодших розрядів множника, тобто по варіантам “А” i “Б” за алгоритмом Лемана засновано на перетворенні у коді Бута сполучення виду 1 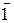 [(1×21)+(-1)×20] на рівнозначну комбінацію 01[(0×21)+(1×20)] i замiщення сполучення
[(1×21)+(-1)×20] на рівнозначну комбінацію 01[(0×21)+(1×20)] i замiщення сполучення 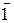 1[(-1)×21+(1×20)] на комбінацію 0
1[(-1)×21+(1×20)] на комбінацію 0 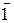 [(0×21)+(-1)×20] (рис.2.12).
[(0×21)+(-1)×20] (рис.2.12).
| Десятковий еквівалент по-точної трипозиційної комбі-нації (Х1Х2Х3) групи цифр множника (МК)
|
|
|
|
|
|
|
|
|
| Поточна трипозиційна ком-бінація (Х1Х2Х3) групи цифр множника (МК)
|   00 0
00 0
| 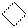  00 1
00 1
| 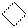  01 0
01 0
|   01 1
01 1
|   10 0
10 0
| 
 10 1 10 1
|   11 0
11 0
|   11 1
11 1
|
| Код Бута – код пари (Х1Х2) трипозиційної групи (Х1Х2Х3) МК
| 
|  0+
0+
|  +-
+-
|  +0
+0
|
 -0 -0
|  -+
-+
|  0-
0-
| 
|
| Код Лемана - код пари (Х1Х2) трипозиційної групи (Х1Х2Х3) МК
| 
|  0+
0+
|  0+
0+
|  +0
+0
|  -0
-0
|  0-
0-
|  0-
0-
| 
|
| Алгоритм множення у поточному циклі за ме-тодом Ле-мана
| Часткові до-бутки у по-точному цик-лі множення
|
(+0)
|
(+РА)
|
(+РА)
|
(+0)
|
(+0)
|
(-РА)
|
(-РА)
|
(+0)
| |
| Зсув МК за парно-одини-чним спосо-бом згідно ал-горитма Лемана
|
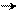 2р 2р
|
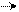 2р 2р
|
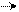 2р 2р
|
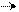 1р 1р
|
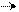 1р 1р
|
 2р 2р
|
 2р 2р
|
 2р 2р
| |
| | | | | | | | | | | | | |
Рисунок 2.12 – Алгоритм множення чисел по варіантам “А” i “Б” за Леманом: РА – регістр множеного
Звідси випливає, що за алгоритмом Лемана кількість значущих цифр (1 і 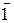 ) у кодi Бута зменшується до мінімальної кількості. Завдяки цьому, якщо доповняльний код множника визначити кодом Лемана, кількість операцій додавання і віднімання множеного зменшується до мінімального і, таким чином, у пристрої для множення чисел досягається прискорення арифметич-ної операції.
) у кодi Бута зменшується до мінімальної кількості. Завдяки цьому, якщо доповняльний код множника визначити кодом Лемана, кількість операцій додавання і віднімання множеного зменшується до мінімального і, таким чином, у пристрої для множення чисел досягається прискорення арифметич-ної операції.
 У разі, коли, наприклад, В = -1011 і
У разі, коли, наприклад, В = -1011 і 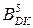 = 1 0101 та (
= 1 0101 та ( 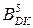 )БУТ =
)БУТ = 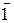 1
1 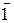 1
1 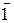 , то зображення
, то зображення 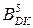 за алгоритмом Лемана (рис.2.12) має вигляд:
за алгоритмом Лемана (рис.2.12) має вигляд:
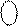 (
( 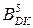 )ЛЕМАН =
)ЛЕМАН = 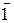 0101.
0101.
Отже, кількість значущих цифр множника 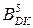 у коді Лемана порівня-но з аналогічним записом множника
у коді Лемана порівня-но з аналогічним записом множника 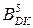 у коді Бута зменшилась з п’яти до трьох.
у коді Бута зменшилась з п’яти до трьох.
У пристрої множення чисел за алгоритмами Лемана_А та Лемана_Б застосовується блок одночасного контролю трьох молодших двійкових цифр регістра множника РВ, які утворюють молодша поточна пара множника [РВ(2)РВ(1)] і додатковий розряд регістра множника РВ(0), який до початку операції множення встановлюється у нульовий стан, що апаратно відображає відсутність у початковому станi значущих цифр за межами найменшого розряду множника (рис.2.13). В процесi множення по варіантам “А” i “Б” при зсуві регістра РВ у бік молодших розрядів на один розряд (1р) у додатковий розряд РВ(0) записується стан тригера РВ(1), а при зсуві РВ на два розряди (2р) – стан тригера РВ(2). Аналіз поточного трипозиційного двійкового коду множника у пристрої здійснюється за допомогою дешифра-тора 3*8 і надалі за вихідними сигналами дешифратора у керуючому автоматі запускаються відповідні процедури утворення часткових добутків за алгоритмом Лемана (рис. 2.14).
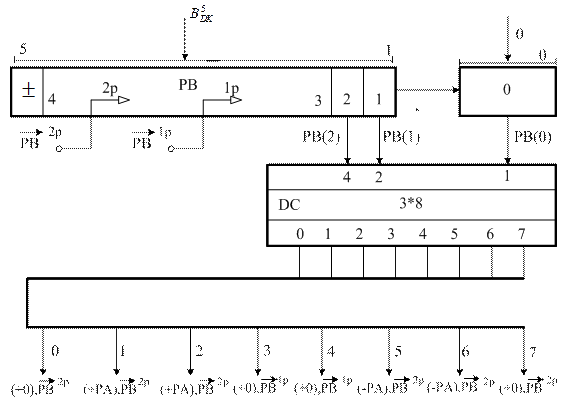
Рисунок 2.13 – Схема аналізатора поточного розряду РВ(1)
множника 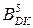 за алгоритмами Лемана_А та Лемана_Б
за алгоритмами Лемана_А та Лемана_Б
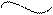
Рисунок 2.14 – Фрагмент мікропрограми пристрою для множення
чисел у доповняльних кодах за алгоритмами Лемана_А та Лемана_Б
| АК
|   РВ РВ
|
|  РА РА
|
  ± ±
| 9 8765 4321
|  ± ±
| 4 3 2 1 0
| ±
| 9 8765 4321
|
 0 0 0000 0000, 0 0 0000 0000,
 1 1 1111 0011, 1 1 1111 0011,
|  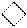  1 0 1 0 1 , 0 1 0 1 0 1 , 0
(+РА)
  2р 2р
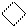  1 1 1 0 1 , 1 1 1 1 0 1 , 1

(+РА)
  2р 2р
 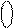 1 1 1 1 1 , 0 1 1 1 1 1 , 0
(-РА)DK
| 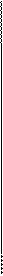 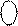 1 1 1111 0011, 1 1 1111 0011,
  2р
1 1 1100 1100, 2р
1 1 1100 1100,
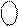  2р
1 1 0011 0000, 2р
1 1 0011 0000,
|
 1 1 1111 0011, 1 1 1111 0011,
 +
1 1 1100 0100, +
1 1 1100 0100,
|
1 1 1011 1111,
 +
0 0 1101 0000, +
0 0 1101 0000,
|
 0 0 1000 1111, 0 0 1000 1111,
|
| | | | | | |
Рисунок 2.15 – Приклад множення чисел у
доповняльних кодах за алгоритмом Лемана_Б
Приклад множення чисел у доповняльних кодах за алгоритмом Лемана_Б подано на рис.2.16.
| Десятковий еквівалент по-точної трипозиційної комбі-нації (Х1Х2Х3) групи цифр множника (МК)
|
|
|
|
|
|
|
|
|
| Поточна трипозиційна ком-бінація (Х1Х2Х3) групи цифр множника (МК)
| 
 00 0 00 0
|   00 1
00 1
|   01 0
01 0
|   01 1
01 1
|   10 0
10 0
|   10 1
10 1
|   11 0
11 0
|   11 1
11 1
|
| Код Бута пари (Х1Х2) три-позиційної групи (Х1Х2Х3) МК
| 
|  0+
0+
|  +-
+-
|
 +0 +0
|  -0
-0
|
 -+ -+
|
 0- 0-
| 
|
| Код Лемана пари (Х1Х2) трипозиційної групи (Х1Х2Х3) МК
| 
|  0+
0+
|  +-
+-
|  +0
+0
|  -0
-0
|  -+
-+
|  0-
0-
| 
|
| Алгоритм множення у поточному циклі за ме-тодом Ле-мана
| Часткові до-бутки у по-точному цик-лі
|
(+0)
|
(+0)
|
(+РА)
|
(+РА)
|
(-РА)
|
(-РА)
|
(+0)
|
(+0)
| |
| Зсув МК за парно-одинич ним спосо-бом за Лема-ном
|
 2р 2р
|
 1р 1р
|
 1р 1р
|
 2р 2р
|
 2р 2р
|
 1р 1р
|
 1р 1р
|
 2р 2р
| |
| | | | | | | | | | | | | |
Рисунок 2.16 – Машинний алгоритм множення
по варіантам “В” i “Г” за Леманом
У пристроях множення чисел за алгоритмами Лемана_В і Лемана_Г ” (рис.2.16) у кожному циклі аналізуються три старших розряди регістра множника (РВ) – поточна пара множника [РВ(5) РВ(4)] і сусідній молодший розряд пари – РВ(3) (рис.2.17). Аналіз трипозиційного коду [РВ(5)РВ(4)РВ(3)] виконується дешифратором 3*8, за вихідними сигналами якого у керуючому автоматі запускаються відповідні мікрооперації за згаданими алгоритмами Лемана (рис.2.18).
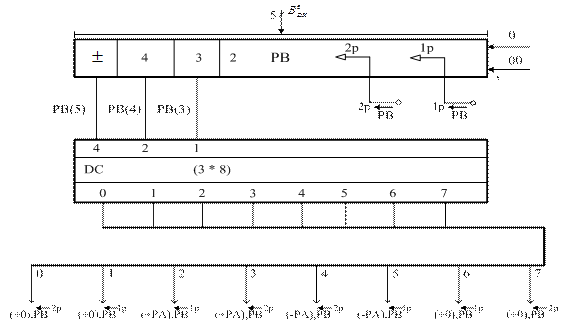
Рисунок 2.17 – Схема аналізатора поточного розряду РВ(5)
множника  за алгоритмами Лемана_В та Лемана_Г
за алгоритмами Лемана_В та Лемана_Г
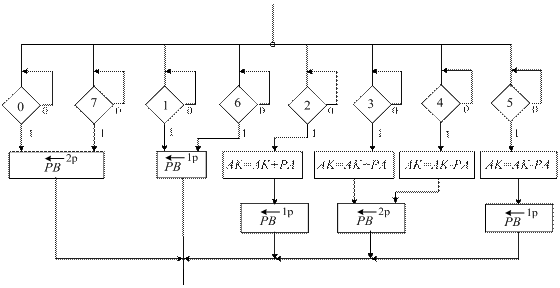
Рисунок 2.18 – Фрагмент мікропрограми пристрою для множення
чисел у доповняльних кодах за алгоритмами Лемана_В та Лемана_Г
Приклад цифрової діаграми множення чисел у доповняльних кодах за алгоритмом Лемана_В подано на рис.2.19.
 АК АК
|  РВ РВ
|
| РА
|
  ± ±
| 9 8765 4321
| ±
| 4 3 2 1
| ±
| 9 8765 4321
|
 0 0 0000 0000, 0 0 0000 0000,
 0 0 0000 1011, 0 0 0000 1011,
|   1 0 0 1 1 , 1 0 0 1 1 ,
= (- РA)
 2р 2р
 0 1 1, 0 0 0 1 1, 0 0
= (+РА)
   2р 2р
1 , 0 0 0 0
= (-РА)
|   1 1 1111 0101, 1 1 1111 0101,
|
 0 0 0000 1011, 0 0 0000 1011,
  + 2р
0 0 0010 1100, + 2р
0 0 0010 1100,
1 1 1111 0101,
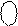
|
0 0 0010 0001,
  + 2р
0 + 2р
0 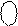 0 1000 0100,
0 0 0000 1011, 0 1000 0100,
0 0 0000 1011,
|
 0 0 1000 1111, 0 0 1000 1111,
|
| | | | | | |
Рисунок 2.19 – Приклад множення чисел в
доповняльних кодах за алгоритмом Лемана_B
2.2.5 Теоретичні засади та структура арифметичних пристроїв для


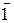 [(1×21)+(-1)×20] на рівнозначну комбінацію 01[(0×21)+(1×20)] i замiщення сполучення
[(1×21)+(-1)×20] на рівнозначну комбінацію 01[(0×21)+(1×20)] i замiщення сполучення 
 00 0
00 0
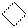
 00 1
00 1

 10 1
10 1
 11 1
11 1
 0+
0+
 +-
+-
 +0
+0
 -0
-0
 -+
-+

 0+
0+
 0+
0+
 +0
+0
 -0
-0
 0-
0-
 2р
2р
 2р
2р
 1р
1р
 У разі, коли, наприклад, В = -1011 і
У разі, коли, наприклад, В = -1011 і 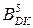 = 1 0101 та (
= 1 0101 та ( 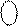 (
( 
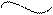


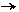 РВ
РВ
 РА
РА

 ±
±
 0 0 0000 0000,
0 0 0000 0000,
 1 1 1111 0011,
1 1 1111 0011,
 1 0 1 0 1 , 0
1 0 1 0 1 , 0

 2р
2р
 1 1 1 0 1 , 1
1 1 1 0 1 , 1
 2р
2р
 1 1 1 1 1 , 0
1 1 1 1 1 , 0
 1 1 1111 0011,
1 1 1111 0011,

 2р
1 1 1100 1100,
2р
1 1 1100 1100,
 2р
1 1 0011 0000,
2р
1 1 0011 0000,
 1 1 1111 0011,
1 1 1111 0011,
 +
1 1 1100 0100,
+
1 1 1100 0100,
 +
0 0 1101 0000,
+
0 0 1101 0000,


 11 0
11 0

 +-
+-
 +0
+0
 -0
-0
 0-
0-
 0+
0+
 2р
2р
 1р
1р
 2р
2р
 1р
1р


 АК
АК
 РВ
РВ

 1 0 0 1 1 ,
1 0 0 1 1 ,
 2р
2р
 0 1 1, 0 0
0 1 1, 0 0
 2р
2р