В арифметичних пристроях для множення чисел у доповняльних кодах за алгоритмом Бута двійковий доповняльний код множника перетворюється у трійкову симетричну знакорозрядну систему числення із базовими симво-лами (1, 0, 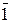 ) згідно із звичайним скороченим записом групи двійкових одиниць:
) згідно із звичайним скороченим записом групи двійкових одиниць:
011112 = 1510 = 1610 – 110 = 100002 – 000012 = 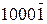 ,
,
де 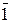 - символ цифри (-1);
- символ цифри (-1);
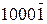 - запис значення групи одиниць множника (01111) у коді Бута.
- запис значення групи одиниць множника (01111) у коді Бута.
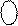 У загальному випадку алгоритм перетворення кожної двійкової цифри числа за алгоритмом Бута подано у табл.2.3, згідно якої, наприклад,
У загальному випадку алгоритм перетворення кожної двійкової цифри числа за алгоритмом Бута подано у табл.2.3, згідно якої, наприклад, 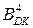 = 0 1101 за Бутом має вигляд:
= 0 1101 за Бутом має вигляд:
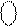


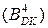 БУТ = ( 0 1101,)БУТ = 1
БУТ = ( 0 1101,)БУТ = 1 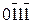 ,
,
де 1 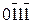 =1×24 + 0×23 + (-1)×22 + 1×21 + (-1)×20=16–4+2–1=13=11012.
=1×24 + 0×23 + (-1)×22 + 1×21 + (-1)×20=16–4+2–1=13=11012.
Отже, за В > 0 подання 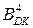 кодом Бута повністю тотожне числовому значенню аргументу В доповняльного коду
кодом Бута повністю тотожне числовому значенню аргументу В доповняльного коду 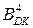 .
.
Звідси випливає, що за шифруванням додатного множника (В > 0) кодом Бута результат множення  на (
на ( 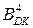 )4БУТ збігається з правильним добутком чисел А і В у доповняльному коді (рис.2.10).
)4БУТ збігається з правильним добутком чисел А і В у доповняльному коді (рис.2.10).
У випадку, коли В<0, то чотирирозрядний доповняльний код множника визначається співвідношенням:
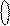
 = (16 + В) = 1
= (16 + В) = 1 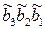 ,
,
де 1 – символ знакового розряду від’ємного множника В у доповняльному коді;
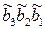 - цифрова частина доповняльного коду
- цифрова частина доповняльного коду 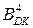 від’ємного множника (В < 0).
від’ємного множника (В < 0).
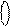 Очевидно, що згідно із загальним правилом утворення коду Бута (табл.2.3) вираз 1
Очевидно, що згідно із загальним правилом утворення коду Бута (табл.2.3) вираз 1 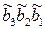 потрібно доповнити зліва і справа незначущими нулями:
потрібно доповнити зліва і справа незначущими нулями:


 1
1 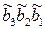 = 0 1
= 0 1 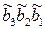 0 .
0 .
Звідси отримаємо:
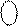
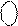





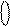
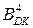 = 1
= 1 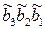 = 0 1
= 0 1 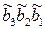 0 = 1 [ X XXX] = 16 + [X XXX],
0 = 1 [ X XXX] = 16 + [X XXX],
де 1 [X XXX] - повний п’ятирозрядний код Бута чотирирозрядного допов-няльного коду 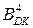 (4/1) від’ємного множника;
(4/1) від’ємного множника;
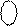 [X XXX] = (
[X XXX] = ( 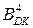 )4БУТ – молодші чотири розряди повного коду Бута від’ємного множника В у доповняльному коді.
)4БУТ – молодші чотири розряди повного коду Бута від’ємного множника В у доповняльному коді.
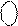 Отже, за умови, коли В<0, справедливе визначення: [X XXX]=(
Отже, за умови, коли В<0, справедливе визначення: [X XXX]=( 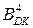 -16), тобто
-16), тобто
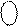 [X XXX] = (
[X XXX] = ( 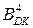 )4БУТ =
)4БУТ = 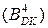 БУТ – 16=
БУТ – 16= 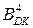 -16=(16+В)–16 = В. ( 2.8 )
-16=(16+В)–16 = В. ( 2.8 )
Таблиця 2.3 - Перетворення цифрових розрядів множника за алгоритмом
Бута
| Комбінація
цифр множника
|    0 0 0 0
| 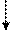   1 1 1 1
| 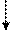   0 1 0 1
|    1 0 1 0
|
| Зображення поточної цифри множника за методом Бута
|
 0 0
|
 0 0
| 
| 
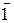
|
| Значення часткового добутку в поточному циклі множення за методом Бута
|
+ 0
|
+ 0
|
+РА
|
-РА
|

 Примітки: РА – регістр множеного;
Примітки: РА – регістр множеного;
0 , 1 – стан поточного розряду множника;
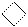
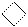 0 , 1 – стан молодшого сусіднього розряду множника.
0 , 1 – стан молодшого сусіднього розряду множника.
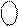 ± ±
| 8 АК 1
| 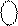 ± ±
| 4 РВ 1
|  ± ±
| 8 РА 1
|
  0 0000 0000, 0 0000 0000,
1 1111 0101,
| 
 0 1101 , 0 1101 ,
РВ(5)БУТ = (+1)
1 1010,
РВ(5)БУТ = 0
1 0100,
РВ(5)БУТ = (-1)
0 1000,
РВ(5)БУТ = (+1)
1 0000,
РВ(5)БУТ = (-1)
| 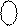 1 1111 0101,
1 1111 0101,
|
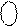 1 1111 0101, 1 1111 0101,
1 1110 1010,
1 1101 0100,
 + +
0 0000 1011,
|
 1 1101 1111, 1 1101 1111,
1 1011 1110,
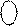 + +
1 1111 0101,
|
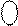 1 1011 0011, 1 1011 0011,
1 0110 0110,
0 0000 1011,
|
 1 0111 0001,
1 0111 0001,
|
Рисунок 2.10 – Приклад множення чисел у доповняльних
кодах за алгоритмом Бута_В:
А = (-1011), В = (+1101), С = (-1000 1111)
 Таким чином, молодші чотири розряди ([ Х ХХХ]) повного коду Бута (1 [ Х ХХХ]) виразу
Таким чином, молодші чотири розряди ([ Х ХХХ]) повного коду Бута (1 [ Х ХХХ]) виразу 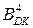 =1
=1 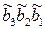 являють собою істинне числове значення від’ємного множника В.
являють собою істинне числове значення від’ємного множника В.
Тоді, наприклад, за умови, коли множник
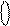
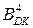 = (-1101)DК = 1 0011,
= (-1101)DК = 1 0011,
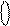
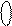

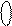 то маємо: B = [(
то маємо: B = [( 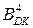 )БУТ]4 = [( 1 0011)БУТ]4 = [ 1
)БУТ]4 = [( 1 0011)БУТ]4 = [ 1 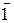 010
010 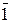 ]4 =
]4 = 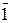 010
010 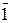 =
=
= [(-1)×24] + (1×22) + [(-1)×20] = (-16) + (+4) + (-1) =-13=(-1101).
Варіант множення чисел у доповняльних кодах за методом Бута для B< 0 подано на рис. 2.11.
 ± ±
| 8 АК 1
|   ± ±
|   4 РВ 1 4 РВ 1
|  0 0
|  ± ±
|  8 РА 1 8 РА 1
|
  0 0000 0000, 0 0000 0000,
 0 0000 1011, 0 0000 1011,
|  1 001 1 , 0 1 001 1 , 0
РВ(1)БУТ = (-1)
1 1 00 1 , 1

РВ(1)БУТ = 0
1 1 1 0 0 , 1
РВ(1)БУТ = (+1)
1 1 1 1 0 , 0
РВ(1)БУТ = 0
 1 1 1 1 1 , 0 1 1 1 1 1 , 0
РВ(1)БУТ = (-1)
|  1 1111 0101, 1 1111 0101,
1 1110 1010,
 1 1101 0100, 1 1101 0100,

 1 1010 1000, 1 1010 1000,
 1 0101 0000, 1 0101 0000,
|
 0 0000 1011, 0 0000 1011,
 +
1 1101 0100, +
1 1101 0100,
|
 1 1101 1111,
1 1101 1111,
 +
0 1011 0000, +
0 1011 0000,
|
 0 1000 1111,
0 1000 1111,
|
Рисунок 2.11 – Приклад множення чисел у доповняльних
кодах за алгоритмом Бута_Б:
А = (-1011), В = (-1101), С = (+1000 1111).
2.2.4 Теоретичні засади та структура арифметичних


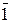 ) згідно із звичайним скороченим записом групи двійкових одиниць:
) згідно із звичайним скороченим записом групи двійкових одиниць: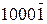 ,
, У загальному випадку алгоритм перетворення кожної двійкової цифри числа за алгоритмом Бута подано у табл.2.3, згідно якої, наприклад,
У загальному випадку алгоритм перетворення кожної двійкової цифри числа за алгоритмом Бута подано у табл.2.3, згідно якої, наприклад, 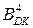 = 0 1101 за Бутом має вигляд:
= 0 1101 за Бутом має вигляд: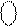


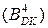 БУТ = ( 0 1101,)БУТ = 1
БУТ = ( 0 1101,)БУТ = 1 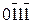 ,
, на (
на ( 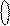
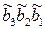 ,
, Очевидно, що згідно із загальним правилом утворення коду Бута (табл.2.3) вираз 1
Очевидно, що згідно із загальним правилом утворення коду Бута (табл.2.3) вираз 1 
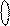
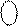
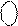


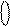
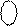 [X XXX] = (
[X XXX] = (  [X XXX] = (
[X XXX] = ( 

 0 0
0 0

 1 1
1 1
 0 1
0 1
 1 0
1 0
 0
0
 0
0


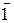

 ±
±
 ±
±
 ±
±
 0 0000 0000,
0 0000 0000,
 0 1101 ,
0 1101 ,




 1 1111 0101,
1 1111 0101,
 1 1111 0101,
1 1111 0101,


 +
+ 1 1101 1111,
1 1101 1111,

 +
+ 1 1011 0011,
1 1011 0011,
 1 0111 0001,
1 0111 0001,

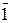 010
010 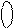

 4 РВ 1
4 РВ 1
 0
0
 8 РА 1
8 РА 1
 0 0000 0000,
0 0000 0000,
 0 0000 1011,
0 0000 1011,
 1 001 1 , 0
1 001 1 , 0










 1 1 1 1 1 , 0
1 1 1 1 1 , 0
 1 1111 0101,
1 1111 0101,


 1 1101 1111,
1 1101 1111,