Принцип роботи пристрою з прискоренням операції множення за груповим методом Робертсона заснований на одночасному визначенні часткового добутку для певної групи розрядів множника.
При визначенні числового значення групи розрядів множника ваговим коефіцієнтам розрядів цифрової частини доповняльного коду приписують природні значення, тобто 1, 2, 4 і т.п. (табл. 2.1). Якщо старший розряд групи являє собою знаковий розряд, то згідно з (2.7) ваговому коефіцієнту цього розряду приписується відповідне від’ємне значення (табл.2.2).
Множення чисел за груповим методом Робертсона може виконуватися по будь-якому із чотирьох базових алгоритмів ("А","Б","В","Г"). При цьому в регістрах пристрою зсув їх вмісту виконується на ту кількість розрядів, які складають довжину цифрової групи множника (рис. 2.6 – 2.7).
Таблиця 2.1 - Визначення часткових добутків дворозрядних числових
груп доповняльного коду множника за алгоритмом Робертсона2
| Група двійкових кодів
|
|
|
|
|
| Десятковий еквівалент двійкової групи
|
|
|
|
|
| Значення част-кового добутку за груповим методом
|
|
РА
|
2РА
| 3РА=
= 2РА+РА =
 = РА + РА = РА + РА
|
Примітка: РА – регістр множеного
Таблиця 2.2 - Визначення часткових добутків “змішаних” дворозрядних числових груп доповняльного коду множника за алгоритмом Робертсона2
Група двійкових кодів
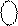 ( ± Х ) ( ± Х )
|
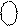 0 0
- + 0 0
- +
|
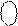 0 1
- + 0 1
- +
|
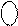 1 0
- + 1 0
- +
|
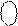 1 1
- + 1 1
- +
|
| Десятковий еквівалент двійкової групи
|
|
|
-2
|
-1
|
| Значення част-кового добутку за груповим методом
|
|
РА
|
-2РА =
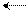 = ( -РА ) = ( -РА )
|
- РА
|
 Примітки: Х - знаковий розряд доповняльного коду множника;
Примітки: Х - знаковий розряд доповняльного коду множника;
Х – старший цифровий розряд доповняльного коду множника
РА – регістр множеного
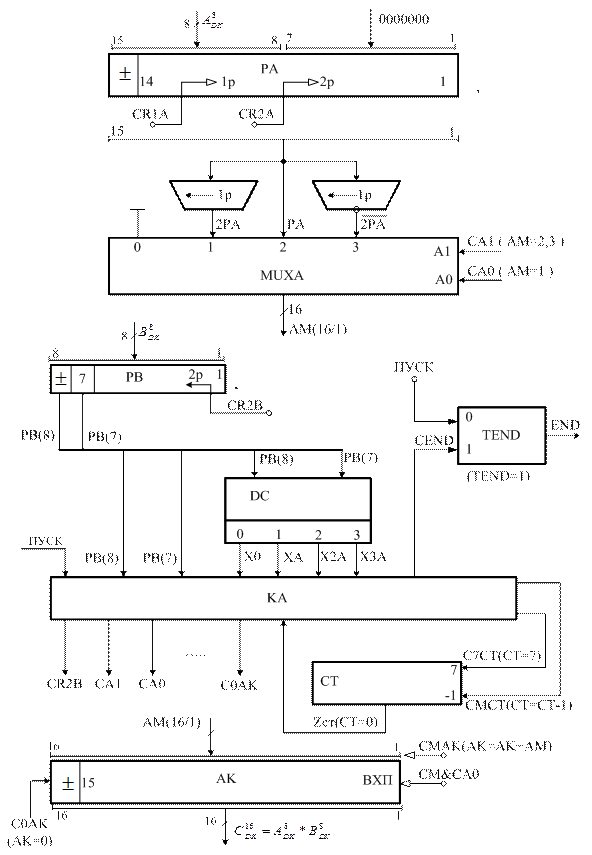
Рисунок 2.6 – Структурна схема арифметичного пристрою
для множення чисел у доповняльних кодах за двопозицiйним
груповим алгоритмом Робертсона2_Г
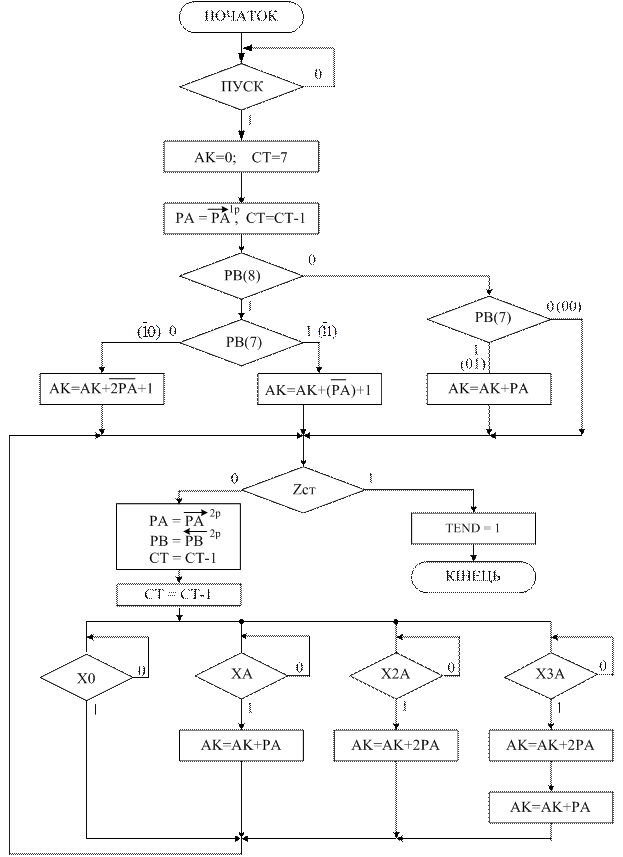
Рисунок 2.7 – Мікропрограма арифметичного пристрою для
множення чисел у доповняльних кодах ( рис.2.6) за двопозицiйним груповим алгоритмом Робертсона2_Г
Приклади множення чисел у доповняльних кодах за груповим алгоритмом Робертсона_Г подано на рис. 2.8 – 2.9.
| Примітки
|   ± ±
| 6 АК 1
|  ± ±
| 3 РВ 1
|  ± ±
| 6 РА 1
|
| 0 =
-2РА =
=-[(-7)DK*8]
|  0 000 000, 0 000 000,
 0 111 000, 0 111 000,
|   1 0 11 , 1 0 11 ,
РВ(4/3) = -2
 2р 2р
1 1 00 ,
 РВ(4/3) = +3 РВ(4/3) = +3
|  1 001 000, 1 001 000,
  1р 1р
 1 100 100,
РА=[(-7)×4)]DK 1 100 100,
РА=[(-7)×4)]DK
 2p 2p
  1 111 001,
РА=(-7)DK 1 111 001,
РА=(-7)DK
|
 [(+7)*8] =
+2PA =+[-7]DK*2 [(+7)*8] =
+2PA =+[-7]DK*2
|  0 111 000,
0 111 000,
1 110 010,
|
 +(7)*6 =
+ РА=[-7]DK = +(7)*6 =
+ РА=[-7]DK =
|  0 101 010,
0 101 010,
 1 111 001, 1 111 001,
|
| +(7*5)DK=
| 0 100 011,
|
Рисунок 2.8 – Приклад множення чисел у доповняльних кодах
за груповим алгоритмом Робертсона2_Г:

 = 1 001 = (-111)DK ;
= 1 001 = (-111)DK ;  = 1 011 = (-101)DK;
= 1 011 = (-101)DK; 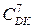 = 0 100 011 = (+100 011)DK
= 0 100 011 = (+100 011)DK
| Примітки
|   ± ±
| 8 АК 1
|   ± D ± D
| 4 РВ 1
|  ± ±
| 8 РА 1
|
| 0 =
-РА =
=-(-13*16)DK
|  0 0000 0000,
0 0 0000 0000,
0  1101 0000, 1101 0000,
|  
 1 1 0101 , 1 1 0101 ,
 РВ(6/5) = -1 РВ(6/5) = -1
 2p 2p
|  1 0011 0000, 1 0011 0000,
PA=(-13*16)DK
 2p 2p
|
 (13*16) =
(+PA)=(-B) DK*4 (13*16) =
(+PA)=(-B) DK*4
|  0 1101 0000, 0 1101 0000,
1 1100 1100,
|  
 0 1 0100 , 0 1 0100 ,
 РВ(6/5) = 1 РВ(6/5) = 1
|  1 1100 1100, 1 1100 1100,
PA=(-13*4)DK
|
 (13*12) =
(+PA) =(-13) DK (13*12) =
(+PA) =(-13) DK
| 0 1001 1100,
1 1111 0011,
|  2p 2p  
 0 1 0000 , 0 1 0000 ,
РВ(6/5) = 1
|  2p 2p
 1 1111 1100, 1 1111 1100,
PA=(-13)DK
|
| (13*11) =
| 0 1000 1111,
|
Рисунок 2.9 – Приклад множення чисел в доповняльних
кодах за двопозиційним груповим алгоритмом Робертсона2_Г:
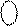
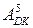 = 1 0011=(-1101)DK;
= 1 0011=(-1101)DK; 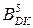 = 1 0101= (-1011)DK;
= 1 0101= (-1011)DK;

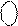
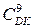 = 0 1000 1111= (+10001111)DK ;
= 0 1000 1111= (+10001111)DK ;
D - додатковий розряд (розшир) цифрової частини множника для утворення цілої кількості груп (із збереженням значення числа)
2.2.3 Теоретичні засади та структура арифметичних пристроїв


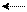 = РА + РА
= РА + РА
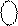 ( ± Х )
( ± Х )
 0 0
- +
0 0
- +
 0 1
- +
0 1
- +
 1 0
- +
1 0
- +
 = ( -РА )
= ( -РА )
 Примітки: Х - знаковий розряд доповняльного коду множника;
Примітки: Х - знаковий розряд доповняльного коду множника;

 ±
±
 ±
±
 0 000 000,
0 000 000,
 0 111 000,
0 111 000,

 1 0 11 ,
1 0 11 ,
 2р
2р
 РВ(4/3) = +3
РВ(4/3) = +3 1 001 000,
1 001 000,
 1р
1р
 1 100 100,
РА=[(-7)×4)]DK
1 100 100,
РА=[(-7)×4)]DK
 2p
2p
 1 111 001,
РА=(-7)DK
1 111 001,
РА=(-7)DK
 0 111 000,
0 111 000,
 +(7)*6 =
+ РА=[-7]DK =
+(7)*6 =
+ РА=[-7]DK =
 0 101 010,
0 101 010,
 1 111 001,
1 111 001,
 = 1 001 = (-111)DK ;
= 1 001 = (-111)DK ;  = 1 011 = (-101)DK;
= 1 011 = (-101)DK; 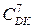 = 0 100 011 = (+100 011)DK
= 0 100 011 = (+100 011)DK
 ± D
± D


 1 1 0101 ,
1 1 0101 ,
 2p
2p
 2p
2p

 (13*12) =
(+PA) =(-13) DK
(13*12) =
(+PA) =(-13) DK
 2p
2p
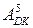 = 1 0011=(-1101)DK;
= 1 0011=(-1101)DK;  = 1 0101= (-1011)DK;
= 1 0101= (-1011)DK;
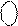
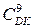 = 0 1000 1111= (+10001111)DK ;
= 0 1000 1111= (+10001111)DK ;