Операційні пристрої для множення чисел в доповняльних кодах призначені для перетворення доповняльних кодів співмножників 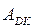 і
і 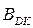 в доповняльний код добутку
в доповняльний код добутку 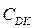 :
:
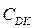 =
= 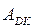 *
* 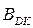 ,
,
де 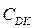 =
= 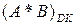 .
.
Для співмножників 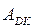 і
і 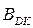 чотирирозрядного пристрою зображення операндів згідно з правилами формування доповняльного коду визначаються за формулами:
чотирирозрядного пристрою зображення операндів згідно з правилами формування доповняльного коду визначаються за формулами:
 = (16 + А)m16;
= (16 + А)m16;  = (16 + B)m16.
= (16 + B)m16.
Операндам пристрою  ,
,  відповідає діапазон подання числових змінних А і В у проміжку між (-8) і (+7). Тому, очевидно, діапазон подання добутку (А * В) визначається інтервалом числової осі між (+64) і (-56). Звідси випливає, що в пристрої множення чотирирозрядних доповняльних кодів
відповідає діапазон подання числових змінних А і В у проміжку між (-8) і (+7). Тому, очевидно, діапазон подання добутку (А * В) визначається інтервалом числової осі між (+64) і (-56). Звідси випливає, що в пристрої множення чотирирозрядних доповняльних кодів  і
і  для машинного подання добутку
для машинного подання добутку 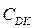 потрібно використовувати восьмирозрядний формат доповняльного коду, тобто для представлення результату потрiбно застосовувати регістр подвійного формату.
потрібно використовувати восьмирозрядний формат доповняльного коду, тобто для представлення результату потрiбно застосовувати регістр подвійного формату.
Машинне зображення позитивного множника в доповняльному коді подається, як відомо, таким же чином, як і в прямому коді, тобто
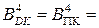 0 MB(3/1) = b3 × 22 + b2 × 21 + b1 × 20,
0 MB(3/1) = b3 × 22 + b2 × 21 + b1 × 20,
де MB(3/1) – трирозрядний модуль додатного множника В;
b3, b2, b1 – двійкові цифри (0 або 1) трирозрядного модуля множника;
22, 21, 20 – вагові коефіцієнти числових розрядів b3, b2 і b1 множника.
Із виразу випливає, що за умови В > 0 добуток 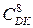 =
= 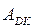 *
* 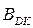 визначається за формулою:
визначається за формулою:
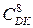 =
=  *
*  =
= 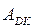 * (b3 × 22 + b2 × 21 + b1 × 20) =
* (b3 × 22 + b2 × 21 + b1 × 20) =
= ( 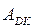 * b3 ) × 22 + (
* b3 ) × 22 + ( 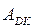 * b2 ) × 21 + (
* b2 ) × 21 + ( 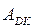 * b1 ) .
* b1 ) .
Звідси випливає, що добуток 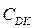 = (
= ( 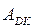 *
* 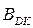 ) визначається сумою часткових добутків Аi =
) визначається сумою часткових добутків Аi = 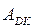 ×bi. При цьому підсумовуються часткові добутки тільки тих розрядів множника, для яких bi = 1. Зазначимо також, що значення кожного значущого часткового добутку пропорційно вазі позиції двійкового множника (bi) і змінюється в два рази при переході від поточого до сусіднього розряду множника. Алгебричне підсумовування часткових добутків Аi може виконуватися за будь-яким із чотирьох базових алгоритмів ("А", "Б" ,"В" ,"Г") з дотриманням звичайних правил додаванням доповняль-них кодів. Один із варіантів множення доповняльних кодів за В > 0 наведено на рис. 2.3.
×bi. При цьому підсумовуються часткові добутки тільки тих розрядів множника, для яких bi = 1. Зазначимо також, що значення кожного значущого часткового добутку пропорційно вазі позиції двійкового множника (bi) і змінюється в два рази при переході від поточого до сусіднього розряду множника. Алгебричне підсумовування часткових добутків Аi може виконуватися за будь-яким із чотирьох базових алгоритмів ("А", "Б" ,"В" ,"Г") з дотриманням звичайних правил додаванням доповняль-них кодів. Один із варіантів множення доповняльних кодів за В > 0 наведено на рис. 2.3.
| Примітки
|   ± ±
| 7 АК 1
|   ± ±
| 3 РВ 1
|  ± ±
| 6 РА 1
|
| 0 =
[(-7)*4]DK =
|  0 0 000 000, 0 0 000 000,
 1 1 100 100, 1 1 100 100, 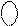
| 0 101 ,
 РВ(4) = 0 РВ(4) = 0
1 010 ,
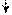 РВ(4) = 1 РВ(4) = 1
0 100 ,
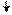 РВ(4) = 0 РВ(4) = 0
1 000 ,
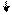 РВ(4) = 1 РВ(4) = 1
|  1 001 000, 1 001 000,
1 100 100,
1 110 010,

 1 111 001, 1 111 001,
|
  [(-7)*4]DK =
[(-7)*1]DK = [(-7)*4]DK =
[(-7)*1]DK =
| 1 1 100 100,
1 1 111 001,
|
|
[(-7)*5]DK =
|  1 1 011 101,
1 1 011 101,
|
Рисунок 2.3 – Приклад множення чисел у доповняльних кодах за алгоритмом “Г “
Якщо В < 0 подання множника В у доповняльному коді має вигляд:
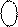
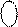
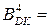 1
1 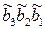 ,
,
де 1 - ознака від’ємних чисел у доповняльному коді;
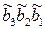 - цифрова частина доповняльного коду від’ємних чисел В.
- цифрова частина доповняльного коду від’ємних чисел В.
Згідно з визначенням доповняльного коду машинне зображення від’ємних чисел В (В = -МВ) обчислюється за формулою:
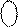
 1
1 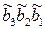 = 16 + В,
= 16 + В,
де (16 + B) < 16.
Із цього виразу випливає, що числова змінна В множника пов’язана з його машинним поданням співвідношенням:
 В = 1
В = 1 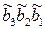 - 16 = 1×23 +
- 16 = 1×23 + 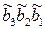 - 16 =
- 16 =
=(- 1)×23 + 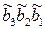 =
= 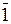
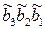 ( 2.7 )
( 2.7 )
де  - позначення цифри (-1) в трійковій системі числення (1, 0,
- позначення цифри (-1) в трійковій системі числення (1, 0,  ).
).
 Звідси, наприклад, для
Звідси, наприклад, для 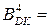 1 011 маємо:
1 011 маємо:
В = 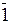 011 = (-1)×23 + 0×22 + 1×21 + 1×20 =
011 = (-1)×23 + 0×22 + 1×21 + 1×20 =
= (-8) + (+2) + (+1) = -510 = -1012 .
Таким чином, згідно з (2.7) множення доповняльних кодів за В<0 потрібно виконувати за співвідношенням:
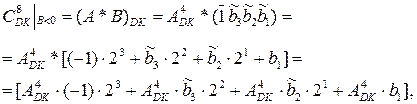
де АDK ×(-1)×23 = (- АDK )×23 – код корекції суми часткових добутків множе-ного  i цифрової частини
i цифрової частини 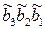 множника
множника  , так званий код коригування суми часткових добутків за Робертсоном.
, так званий код коригування суми часткових добутків за Робертсоном.
Підсумовування часткових добутків ( 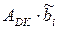 ) може виконуватися звичайним способом за будь-яким із чотирьох базових алгоритмів ("А", "Б", "В", "Г") iз дотриманням звичайних правил додавання доповняльних кодів. Код корекції Робертсона (-
) може виконуватися звичайним способом за будь-яким із чотирьох базових алгоритмів ("А", "Б", "В", "Г") iз дотриманням звичайних правил додавання доповняльних кодів. Код корекції Робертсона (-  )DK (при NB=1)формується за співвідношен-ням:
)DK (при NB=1)формується за співвідношен-ням:
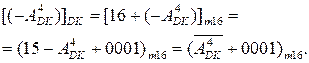
Варіант множення доповняльних кодів за алгоритмом Робертсона при B< 0 подано на рис.2.4.
| Примітки
| 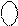  ± ±
| 7 АК 1
|   ± ±
|  3 РВ 1 3 РВ 1
|   ± ±
| 3 РА 1
|
 0 =
[(-7)*8/8]DK = 0 =
[(-7)*8/8]DK =
| 0 0 000, 000
 1 1 001, 1 1 001,
| 1 01 1 ,
 РВ(1) = 1 РВ(1) = 1
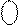   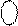
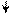 1 1 0 1 ,
РВ(1) = 1 1 1 0 1 ,
РВ(1) = 1
 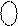   1 1 1 0 , 1 1 1 0 ,
РВ(1) = 0
     1 1 1 1 , 1 1 1 1 ,
РВ(1) = -1
| 1 001,
|
[(-7)*8/8]DK =
 [(-7)*4/8]DK =
[(-7)*8/8]DK = [(-7)*4/8]DK =
[(-7)*8/8]DK =
| 1   1 001, 000 1 001, 000
 1 1 100, 100 1 1 100, 100
 1 1 001, 1 1 001,
|
[(-7)*12/8]DK =
[(-7)*6/8]DK =
 [(-7)*3/8]DK =
[(+7)*8/8]DK = [(-7)*3/8]DK =
[(+7)*8/8]DK =
| 1 0 101, 100

 1 1 010, 110 1 1 010, 110
1 1 101, 011
 0 0 111, 0 0 111,
|
[(+7)*5/8]DK =
 *23
(+7)*5 =35 = *23
(+7)*5 =35 =
|  0 0 100, 011 0 0 100, 011
 *23
0 0 100 011, *23
0 0 100 011,
|
Рисунок 2.4 – Приклад множення чисел у доповняльних кодах за алгоритмом Робертсона_А: (В (множник) < 0, А (множене)< 0)
Структурна схема пристрою для множення чисел у доповняльних кодах за алгоритмом «А» із корекцією результату за алгоритмом Робертсона подана на рис.2.5.
При кожному зверненні до блока множення подається сигнал «Пуск». За сигналом «Пуск» керуючий автомат (КА) перемикається в активний стан і формує початкові керуючі сигнали С0АК і С3СТ, за якими онуляється акуму-лятор (за сигналом С0АК) і лічильник (СТ) перемикається в початковий стан (за сигналом С3СТ). Потім у залежності від поточного стану змінної РВ(1) у кожному циклі множення до акумулятора додається код нуля або вміст регістра А (тобто  ). Кожний цикл закінчується зсувом акумулятора АК-РС і регістра множника РВ вправо, а вміст лічильника зменшується на одиницю. Після вичерпання цифрової частини множника ознака нуля лічильника встановлюється у стан «1». За цим сигналом у наступному циклі множення за РВ(1)=1 до акумулятора додається
). Кожний цикл закінчується зсувом акумулятора АК-РС і регістра множника РВ вправо, а вміст лічильника зменшується на одиницю. Після вичерпання цифрової частини множника ознака нуля лічильника встановлюється у стан «1». За цим сигналом у наступному циклі множення за РВ(1)=1 до акумулятора додається 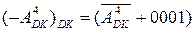 , тобто виконується корекція результату множення доповняльного коду множеного на цифрову частину
, тобто виконується корекція результату множення доповняльного коду множеного на цифрову частину 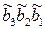 доповняльного коду множника
доповняльного коду множника  .
.
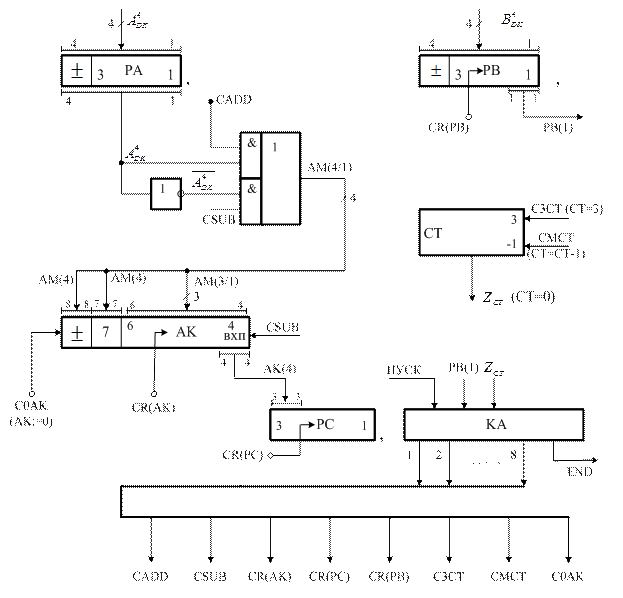
Рисунок 2.5 – Структурна схема арифметичного пристрою для
множення чисел у доповняльних кодах по варiанту “А” з
корекцією (виправленням) результату за методом Робертсона


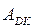 і
і 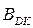 в доповняльний код добутку
в доповняльний код добутку 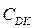 :
: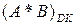 .
. = (16 + А)m16;
= (16 + А)m16;  = (16 + B)m16.
= (16 + B)m16.
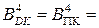 0 MB(3/1) = b3 × 22 + b2 × 21 + b1 × 20,
0 MB(3/1) = b3 × 22 + b2 × 21 + b1 × 20,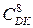 =
= 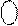
 ±
±

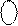 ±
±
 0 0 000 000,
0 0 000 000,
 1 1 100 100,
1 1 100 100, 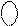
 РВ(4) = 0
РВ(4) = 0

 РВ(4) = 1
РВ(4) = 1

 РВ(4) = 0
РВ(4) = 0

 РВ(4) = 1
РВ(4) = 1 1 001 000,
1 001 000,


 1 111 001,
1 111 001,
 1 1 011 101,
1 1 011 101,
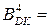 1
1 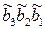 ,
,
 В = 1
В = 1 
 - позначення цифри (-1) в трійковій системі числення (1, 0,
- позначення цифри (-1) в трійковій системі числення (1, 0,  Звідси, наприклад, для
Звідси, наприклад, для 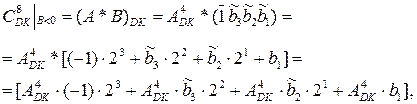
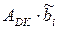 ) може виконуватися звичайним способом за будь-яким із чотирьох базових алгоритмів ("А", "Б", "В", "Г") iз дотриманням звичайних правил додавання доповняльних кодів. Код корекції Робертсона (-
) може виконуватися звичайним способом за будь-яким із чотирьох базових алгоритмів ("А", "Б", "В", "Г") iз дотриманням звичайних правил додавання доповняльних кодів. Код корекції Робертсона (- 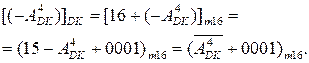
 3 РВ 1
3 РВ 1
 0 =
[(-7)*8/8]DK =
0 =
[(-7)*8/8]DK =
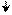 РВ(1) = 1
РВ(1) = 1

 1 1 0 1 ,
РВ(1) = 1
1 1 0 1 ,
РВ(1) = 1




 [(-7)*4/8]DK =
[(-7)*8/8]DK =
[(-7)*4/8]DK =
[(-7)*8/8]DK =
 1 001, 000
1 001, 000
 1 1 001,
1 1 001, [(-7)*3/8]DK =
[(+7)*8/8]DK =
[(-7)*3/8]DK =
[(+7)*8/8]DK =

 1 1 010, 110
1 1 010, 110

 0 0 111,
0 0 111,
 *23
(+7)*5 =35 =
*23
(+7)*5 =35 =
 0 0 100, 011
0 0 100, 011
 *23
0 0 100 011,
*23
0 0 100 011,
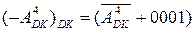 , тобто виконується корекція результату множення доповняльного коду множеного на цифрову частину
, тобто виконується корекція результату множення доповняльного коду множеного на цифрову частину 