МС(А) = 24 * МСS(А), ( 2.3 )
де МСS(А) = МС/24 = (c8c7c6c5, c4c3c2c1) – проміжна змішана сума часткових добутків;
(с8 – с5) – ціла частина МСS(А);
(с4 – с1) – дробова частина МСS(А);
МСS(А) = ((((0 + А1)×2-1 + А2)×2-1 + А3)×2-1 + А4)×2-1;
А1 = МА× b1; А2 = МА× b2; А3 = МА× b3; А4 = МА× b4 - часткові добутки (добутки множеного на відповідний біт множника).
 Рисунок 2.1,а – Узагальнена структурна схема для множення
Рисунок 2.1,а – Узагальнена структурна схема для множення
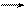
 чисел в прямих кодах за алгоритмом «А» ( РВ, РС)
чисел в прямих кодах за алгоритмом «А» ( РВ, РС)
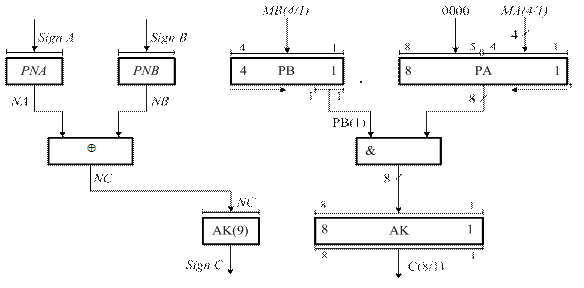
Рисунок 2.1,б – Узагальнена структурна схема для множення

 чисел в прямих кодах за алгоритмом «Б» ( РВ, РА)
чисел в прямих кодах за алгоритмом «Б» ( РВ, РА)
Таким чином, за алгоритмом «А» часткові добутки визначаються шляхом множення поточного стану молодшого розряду регістра множника РВ(1) і множеного. Цикл закінчується зсувом множника та часткової суми МСS вправо. Зсувом МСS вправо на один розряд здійснюється множення часткової суми МСS на 2-1 за алгоритмом (2.3). Старші розряди суми част-кових добуткiв (с8–с5) обчислюються з використанням регістра – акумуля-тора (АК(8/5), а молодша тетрада добутку (с4–с1) накопичується у звичайно-му зсувному регістрі РС(4/1) при одночасному зсувi вправо регістра-акамулятора АК i регістра РС. Знак добутку NC згідно з (2.1) визначається суматором за модулем два знаків співмножників NА і NB. Після закінчення операції знак добутку NС записується у старший розряд регістра – акумуля-тора АК(9). Множення суми часткових добуткiв на коефiцiєнт 24 здійснюєть-ся уявним перенесенням коми в регiстрi РС на чотири розряди вправо (рис.2.1,а).
В операційних пристроях для множення модулів по алгоритму “Б” (рис.2.1,б) обчислення добутку здійснюється за формулою:
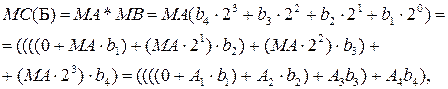 ( 2.4 )
( 2.4 )
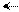
 де А1 = МА; А2 = А1×21 = А1 ; А3 = А2×21 = А2 ; А4 = А3×21 = А3 ;
де А1 = МА; А2 = А1×21 = А1 ; А3 = А2×21 = А2 ; А4 = А3×21 = А3 ;
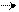
 Таким чином, за алгоритмом “Б” множення модулів чисел виконується при нерухомій сумі часткових добутків шляхом послідовного множення поточного стану молодшого розряду регістра множника РВ(1) і вмісту регістра множеного РА. У кожному циклі операції множення регістр множника РВ зсувається вправо (В ), а регістр множеного РА – вліво (А). Шляхом зсуву вліво множеного РА у кожному циклі здійснюється послідовне множення вмісту регістра множеного РА на 2+1.
Таким чином, за алгоритмом “Б” множення модулів чисел виконується при нерухомій сумі часткових добутків шляхом послідовного множення поточного стану молодшого розряду регістра множника РВ(1) і вмісту регістра множеного РА. У кожному циклі операції множення регістр множника РВ зсувається вправо (В ), а регістр множеного РА – вліво (А). Шляхом зсуву вліво множеного РА у кожному циклі здійснюється послідовне множення вмісту регістра множеного РА на 2+1.
В операційних пристроях для множення чисел у прямих кодах по алгоритму “В” (рис.2.1,в) послідовне підсумовування часткових добутків здійснюється за формулою:
МС(В) 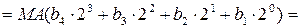
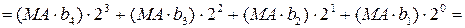
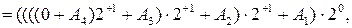 ( 2.5 )
( 2.5 )
де А4 = МА× b4; А3 = МА× b3; А2 = МА× b2; А1 = МА× b1.
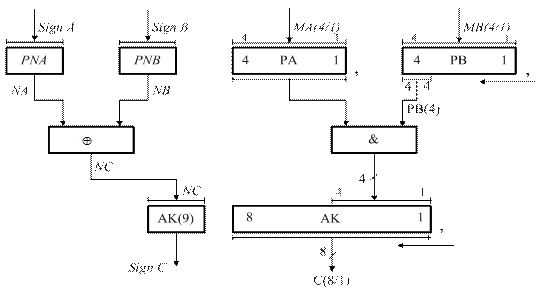
 Рисунок 2.1,в – Узагальнена структурна схема для множення
Рисунок 2.1,в – Узагальнена структурна схема для множення
 чисел в прямих кодах за алгоритмом «В» ( РВ, АК ).
чисел в прямих кодах за алгоритмом «В» ( РВ, АК ).
Таким чином, за алгоритмом «В» множення чисел виконується при нерухомому (відносно позиції коми) множеному (РА) шляхом послідовного множення поточного стану старшого розряду множника РВ(4) і вмісту регістра множеного (РА). У кожному циклі операції множення регістр множника РВ і регістр-акумулятор часткової суми АК зсуваються вліво (РВ, АК). Шляхом зсуву вліво регістра-акумулятора у кожному циклі здійснюється множення суми часткових добутків на 2+1.
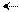
 В операційних пристроях для множення чисел у прямих кодах по алгоритму “Г” (рис.2.1,г) послідовне додавання часткових добутків здійсню-ється за формулою:
В операційних пристроях для множення чисел у прямих кодах по алгоритму “Г” (рис.2.1,г) послідовне додавання часткових добутків здійсню-ється за формулою:
МС(Г) 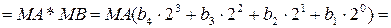
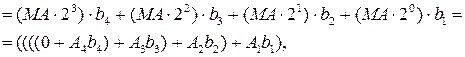 ( 2.6 )
( 2.6 )
де А4 = (МА×2+4)×2-1; А3 = А4 × 2-1; А2 = А3 × 2-1; А1 = А2 × 2-1;
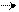 Таким чином, множення модулів прямих кодів за алгоритмом “Г” виконується при нерухомому (відносно позиції коми) регістрі-акумуляторі (АК) шляхом послідовного множення поточного стану старшого розряду множника РВ(4) і вмісту поточного стану зсувного регістра множеного РА. У кожному циклі операції регістр множника РВ зсувається вліво (відносно припустимого положення коми), а регістр множеного – вправо (РА). Шляхом зсуву вправо регістра множеного РА у кожному циклі здійснюється множення множеного на 2-1.
Таким чином, множення модулів прямих кодів за алгоритмом “Г” виконується при нерухомому (відносно позиції коми) регістрі-акумуляторі (АК) шляхом послідовного множення поточного стану старшого розряду множника РВ(4) і вмісту поточного стану зсувного регістра множеного РА. У кожному циклі операції регістр множника РВ зсувається вліво (відносно припустимого положення коми), а регістр множеного – вправо (РА). Шляхом зсуву вправо регістра множеного РА у кожному циклі здійснюється множення множеного на 2-1.
 Рисунок 2.1,г – Узагальнена структурна схема для множення
Рисунок 2.1,г – Узагальнена структурна схема для множення
чисел в прямих кодах за алгоритмом «Г» (РА, РВ)
Приклади множення чисел у прямих кодах за базовими алгоритмами "А", "Б", "В" і "Г" подано на рис.2.2.
| Примітки
|   ± ±
| 8 АК 1
|  ± ±
| 4 РВ 1
|  ± ±
| 4 РА 1
|
 0 =
13*16 / 16 = 0 =
13*16 / 16 =
| 0 0000, 0000
 0 1101, 0 1101,
|   ± 101 1 , ± 101 1 ,
 РВ(1) = 1 РВ(1) = 1
   ± 010 1 , ± 010 1 ,
РВ(1) = 1

±   001 0 , 001 0 ,
 РВ(1) = 0 РВ(1) = 0
  ± 000 1 , ± 000 1 ,
РВ(1) = 1
|  ± 1101, ± 1101,
|
13*16 / 16 =
  13*8 / 16 =
13*16 / 16 = 13*8 / 16 =
13*16 / 16 =
| 0   1101, 0000 1101, 0000
0  0110, 1000 0110, 1000
0  1101, 1101,
|
13*24 / 16 =
13*12 / 16 =
 13*6 / 16 =
13*16 / 16 =
13*22 / 16 = 13*6 / 16 =
13*16 / 16 =
13*22 / 16 =
 13*11 / 16 =
*24
(13 * 11) = 13*11 / 16 =
*24
(13 * 11) =
 = =
| 1 0011, 1000
   0 1001, 1100 0 1001, 1100
  0 0100, 1110
0 1101, 0 0100, 1110
0 1101,
|
 1 0001, 1110 1 0001, 1110
0  1000, 1111 1000, 1111
 *24 *24
0  1000 1111, 1000 1111,
NС 1000 1111,
|
Рисунок 2.2,а – Приклад множення чисел у прямих кодах за алгоритмом “А”
| Примітки
|  ± ±
| 8 АК 1
|  ± ±
| 4 РВ 1
|  ± ±
| 8 РА 1
|
 0 =
(13) = 0 =
(13) =
|  0 0000 0000, 0 0000 0000,
 0 0000 1101, 0 0000 1101,
|   ± 101 1 , ± 101 1 ,
 РВ(1) = 1 РВ(1) = 1

  ± 010 1 , ± 010 1 ,
 РВ(1) = 1 РВ(1) = 1
± 001 0 ,
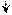 РВ(1) = 0 РВ(1) = 0

  ± 000 1 , ± 000 1 ,
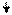 РВ(1) = 1 РВ(1) = 1
| ±  0000 1101, 0000 1101,
 ±
± 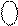 0001 1010, 0001 1010,
±  0011 0100, 0011 0100,

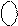 ± 0110 1000, ± 0110 1000,
|
 (13) =
(13*2) = (13) =
(13*2) =
|  0 0000 1101, 0 0000 1101,
 0 0001 1010, 0 0001 1010,
|
 (13*3) =
(13*8) = (13*3) =
(13*8) =
| 
 0 0010 0111,
0 0110 1000, 0 0010 0111,
0 0110 1000,
|
(13*11) =
 = =
|  0 1000 1111, 0 1000 1111,
 NС 1000 1111,
NС 1000 1111,
|
Рисунок 2.2,б – Приклад множення чисел у прямих кодах за алгоритмом “Б”
| Примітки
|   ± ±
| 8 АК 1
|  ± ±
| 4 РВ 1
|  ± ±
| 4 РА 1
|
 0 =
(13) 0 =
(13)
| 0 0000 0000,
1101,
|   ± 1 011 , ± 1 011 ,
 РВ(4) = 1 РВ(4) = 1

  ± 0 110 , ± 0 110 ,
 РВ(4) = 0 РВ(4) = 0
± 1 100 ,
 РВ(4) = 1 РВ(4) = 1
±  1 000 , 1 000 ,
 РВ(4) = 1 РВ(4) = 1
|  ± 1101, ± 1101,
|
(13) =
(13*2) =
 (13*4) =
(13) (13*4) =
(13)
| 0   0000 1101, 0000 1101,
0 0001 1010,
0 0011 0100,
 1101, 1101,
|
(13*5) =
 (13*10) =
(13) (13*10) =
(13)
| 0  0100 0001, 0100 0001,
 0 1000 0010,
1101, 0 1000 0010,
1101,
|
(13 * 11) =
 = =
|  0 1000 1111,
0 1000 1111,
 NС 1000 1111,
NС 1000 1111,
|
Рисунок 2.2,в – Приклад множення чисел у прямих кодах за алгоритмом “В”
| Примітки
|   ± ±
| 8 АК 1
|  ± ±
| 4 РВ 1
|  ± ±
| 8 РА 1
|
 0 =
(13*8)= 0 =
(13*8)=
| 0 0000 0000,
 0 0110 1000, 0 0110 1000,
|   ± 1 011 , ± 1 011 ,
 РВ(4) = 1 РВ(4) = 1
  ± 0 110 , ± 0 110 ,
 РВ(4) = 0 РВ(4) = 0
± 1 100 ,
 РВ(4) = 1 РВ(4) = 1

  ± 1 000 , ± 1 000 ,
 РВ(4) = 1 РВ(4) = 1
| ± 1101  0000, 0000,
 ±
±  0110 1000, 0110 1000,
±  0011 0100, 0011 0100,
± 0001 1010,
 ± 0000 1101, ± 0000 1101,
|
 (13*8) =
(13*2) = (13*8) =
(13*2) =
|  0 0110 1000,
0 0001 1010, 0 0110 1000,
0 0001 1010,
|
 (13*10) =
(13) = (13*10) =
(13) =
| 
 0 1000 0010,
0 0000 1101, 0 1000 0010,
0 0000 1101,
|
(13*11) =
 = =
| 0 1000 1111,
 NС 1000 1111,
NС 1000 1111,
|
Рисунок 2.2,г – Приклад множення чисел у прямих кодах
за алгоритмом “Г”
2.2 Теоретичні засади та структура арифметичних пристроїв для множення чисел у доповняльних кодах


 Рисунок 2.1,а – Узагальнена структурна схема для множення
Рисунок 2.1,а – Узагальнена структурна схема для множення
 чисел в прямих кодах за алгоритмом «А» ( РВ, РС)
чисел в прямих кодах за алгоритмом «А» ( РВ, РС)

 чисел в прямих кодах за алгоритмом «Б» ( РВ, РА)
чисел в прямих кодах за алгоритмом «Б» ( РВ, РА)
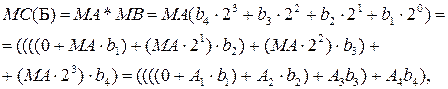 ( 2.4 )
( 2.4 )
 Таким чином, за алгоритмом “Б” множення модулів чисел виконується при нерухомій сумі часткових добутків шляхом послідовного множення поточного стану молодшого розряду регістра множника РВ(1) і вмісту регістра множеного РА. У кожному циклі операції множення регістр множника РВ зсувається вправо (В ), а регістр множеного РА – вліво (А). Шляхом зсуву вліво множеного РА у кожному циклі здійснюється послідовне множення вмісту регістра множеного РА на 2+1.
Таким чином, за алгоритмом “Б” множення модулів чисел виконується при нерухомій сумі часткових добутків шляхом послідовного множення поточного стану молодшого розряду регістра множника РВ(1) і вмісту регістра множеного РА. У кожному циклі операції множення регістр множника РВ зсувається вправо (В ), а регістр множеного РА – вліво (А). Шляхом зсуву вліво множеного РА у кожному циклі здійснюється послідовне множення вмісту регістра множеного РА на 2+1.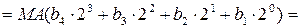
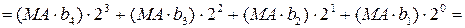
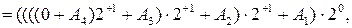 ( 2.5 )
( 2.5 )
 Рисунок 2.1,в – Узагальнена структурна схема для множення
Рисунок 2.1,в – Узагальнена структурна схема для множення чисел в прямих кодах за алгоритмом «В» ( РВ, АК ).
чисел в прямих кодах за алгоритмом «В» ( РВ, АК ).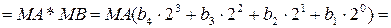
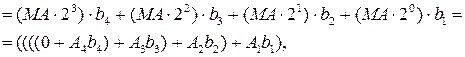 ( 2.6 )
( 2.6 )
 ±
±
 ±
±
 0 =
13*16 / 16 =
0 =
13*16 / 16 =
 0 1101,
0 1101,

 РВ(1) = 1
РВ(1) = 1

 ± 010 1 ,
± 010 1 ,


 001 0 ,
001 0 , РВ(1) = 0
РВ(1) = 0
 ± 000 1 ,
± 000 1 , 13*8 / 16 =
13*16 / 16 =
13*8 / 16 =
13*16 / 16 =
 1101, 0000
1101, 0000
 0110, 1000
0110, 1000 1101,
1101, 13*6 / 16 =
13*16 / 16 =
13*22 / 16 =
13*6 / 16 =
13*16 / 16 =
13*22 / 16 =
 13*11 / 16 =
*24
(13 * 11) =
13*11 / 16 =
*24
(13 * 11) =
 =
=
 0 1001, 1100
0 1001, 1100
 0 0100, 1110
0 1101,
0 0100, 1110
0 1101,
 1 0001, 1110
1 0001, 1110

 1000, 1111
1000, 1111 1000 1111,
1000 1111, ±
±
 0 =
(13) =
0 =
(13) =
 0 0000 0000,
0 0000 0000,

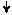 РВ(1) = 1
РВ(1) = 1


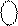 ± 010 1 ,
± 010 1 ,
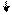 РВ(1) = 1
РВ(1) = 1

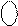

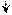 РВ(1) = 0
РВ(1) = 0
 ± 000 1 ,
± 000 1 ,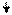 РВ(1) = 1
РВ(1) = 1 ±
± 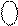 0001 1010,
0001 1010,
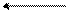

 ± 0110 1000,
± 0110 1000, 0 0000 1101,
0 0000 1101,
 0 0001 1010,
0 0001 1010,
 0 0010 0111,
0 0110 1000,
0 0010 0111,
0 0110 1000,
 0 1000 1111,
0 1000 1111,
 NС 1000 1111,
NС 1000 1111,
 ± 1 011 ,
± 1 011 ,
 РВ(4) = 1
РВ(4) = 1

 ± 0 110 ,
± 0 110 ,
 РВ(4) = 0
РВ(4) = 0


 1 000 ,
1 000 , РВ(4) = 1
РВ(4) = 1 0000 1101,
0000 1101,
 1101,
1101, 0100 0001,
0100 0001,
 0 1000 1111,
0 1000 1111,
 NС 1000 1111,
NС 1000 1111,

 РВ(4) = 0
РВ(4) = 0



 РВ(4) = 1
РВ(4) = 1 ±
± 

 ± 0000 1101,
± 0000 1101,