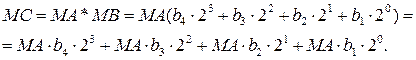На завершення розглянемо типові приклади додавання чисел з негативним нулем (рис.1.46).
Припустімо, що потрібно обчислити суму 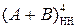 за таких аргументів: А = - 010; В = - 011. За цих умов числовий вираз стану суматора SM НН(А+В) (рис.1.46) визначається за формулою:
за таких аргументів: А = - 010; В = - 011. За цих умов числовий вираз стану суматора SM НН(А+В) (рис.1.46) визначається за формулою:


 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 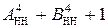 ]5 =
]5 =
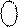 = [ 0 101 + 0 100 + 1]5 = (1010)5 = 0 1 010,
= [ 0 101 + 0 100 + 1]5 = (1010)5 = 0 1 010,
де NS = 1; EN = 0; S3S2S1 = 010;
ПП(А-В) = 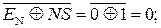


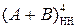 = EN S3S2S1 = 0 010 = (-101)
= EN S3S2S1 = 0 010 = (-101) 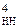 .
.


 Припустімо далі, що потрібно обчислити суму
Припустімо далі, що потрібно обчислити суму 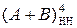 за таких аргументів: А = - 110; В = -101. За цих умов отримаємо: EN NS S3S2S1 = [
за таких аргументів: А = - 110; В = -101. За цих умов отримаємо: EN NS S3S2S1 = [ 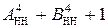 ]5 =
]5 =
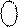 = [ 0 001 + 0 010 + 1]5 = (0100)5 = 0 0 100,
= [ 0 001 + 0 010 + 1]5 = (0100)5 = 0 0 100,
де EN = 0; NS = 0; S3S2S1 = 100;
ПП(А+В) = 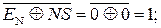
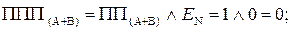
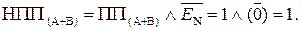
Отже, за цих значень аргументів виникає негативне переповнення розрядної сітки SMНН(А+В).
Розглянемо тепер алгоритм визначення різниці чисел (А - В) на основі кодів з негативним нулем.
Згідно з загальним правилом обчислення коду чисел з негативним нулем різниця чисел 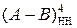 повинна обчислюватися за формулою:
повинна обчислюватися за формулою:
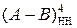 = 7 +( А - В) .
= 7 +( А - В) .
Для спрощення схеми формувача різниці чисел (А - В) співвідношення перетворимо наступним чином:
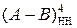 = (7 + А) - (7 + В) + 7 = (
= (7 + А) - (7 + В) + 7 = ( 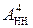 -
- 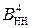 + 7 + 16)m16 =
+ 7 + 16)m16 =
= ( 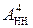 + 15 -
+ 15 - 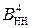 + 8)m16 =((
+ 8)m16 =(( 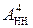 +
+ 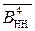 )m16 + 1000) m16, (1.139)
)m16 + 1000) m16, (1.139)
де 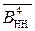 - порозрядне інверсне значення коду
- порозрядне інверсне значення коду 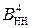 .
.
Через те, що аргументи функцій 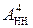 і
і 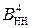 визначені у діапазоні числової осі від (-7) до (+8), функція
визначені у діапазоні числової осі від (-7) до (+8), функція 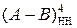 однозначно визначена також у проміжку між (-7) і (+8), тому при відніманні чисел можливе переповнення функції (1.139).
однозначно визначена також у проміжку між (-7) і (+8), тому при відніманні чисел можливе переповнення функції (1.139).
Позитивне переповнення різниці 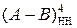 виникає у тому випадку, коли А = + МА, В = - МВ, тобто (А - В) = (МА + МВ) і сумісно (МА + МВ) = (9 ¸ 16). У цьому випадку повна п’ятирозрядна сума на виходах SMНН(А-В) (рис.1.47) складає код:
виникає у тому випадку, коли А = + МА, В = - МВ, тобто (А - В) = (МА + МВ) і сумісно (МА + МВ) = (9 ¸ 16). У цьому випадку повна п’ятирозрядна сума на виходах SMНН(А-В) (рис.1.47) складає код:

 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 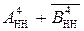 ]5 =
]5 =
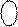
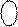 =7 + А + 15 – (7 + В) = 15 + (А – В) =15 + (МА + МВ) =
=7 + А + 15 – (7 + В) = 15 + (А – В) =15 + (МА + МВ) =
 =15 + (9 ¸ 16) =
=15 + (9 ¸ 16) =  = 24 ¸ 31 = 1 1 000 ¸ 1 1 110,
= 24 ¸ 31 = 1 1 000 ¸ 1 1 110,
де EN = 1; NS = 1.
Таким чином, за наявності ознаки ППП(А-В) = 1 маємо EN NS = 11, тобто функцію ППП(А-В) потрібно обчислювати за формулою:
ППП(А-В) = 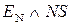 .
.
Негативне переповнення (НПП) функції 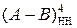 , очевидно, може виникати в тому випадку, коли А = - МА, В = + МВ, (А - В) = -(МА + МВ) = =(-8) ¸ (-14).
, очевидно, може виникати в тому випадку, коли А = - МА, В = + МВ, (А - В) = -(МА + МВ) = =(-8) ¸ (-14).
Тоді на виходах SMНН(А-В) (рис.1.47) отримаємо :

 EN NS S3S2S1 = [15 – (МА + МВ)]5 =[15 - (8 ¸ 14)]5 = (7 ¸ 1)5 =
EN NS S3S2S1 = [15 – (МА + МВ)]5 =[15 - (8 ¸ 14)]5 = (7 ¸ 1)5 =
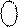


 = (111 ¸ 001)5 = 0 0 111 ¸ 0 0 001,
= (111 ¸ 001)5 = 0 0 111 ¸ 0 0 001,
Таким чином, за наявності ознаки НПП(А-В) = 1 маємо EN NS = 00, тобто функцію НПП(А-В) потрібно визначити за формулою:
НПП(А-В) = 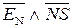 .
.
З цих міркувань випливає:
ПП(А-В) = ППП(А-В) 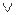 НПП(А-В) =
НПП(А-В) = 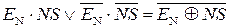 , (1.140)
, (1.140)
причому ППП(А-В) = ПП(А-В) 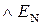 , НПП(А-В) = ПП(А-В)
, НПП(А-В) = ПП(А-В) 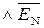 .
.
Таким чином, згідно з (1.137) і (1.140) ознака переповнення розрядної сітки SMНН(А+В) і SMНН(А-В) формується за еквівалентними булевими вираза-ми, що спрощує побудову об’єднаного блоку SMНН(А+В) / SMНН(А-В).
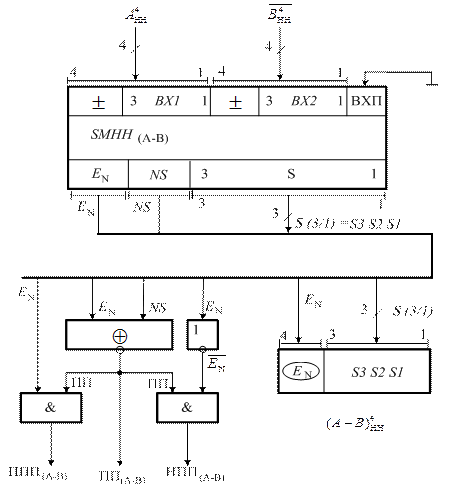
Рисунок 1.47 – Структурна схема суматора для
віднімання чисел у кодах з негативним нулем
Остаточно різниця 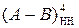 згідно з (1.139) формується за правилом:
згідно з (1.139) формується за правилом:



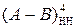 = [(EN NS S3S2S1)m16 + 1000]m16 =
= [(EN NS S3S2S1)m16 + 1000]m16 =
 = [ NS S3S2S1 + 1000]m16 =
= [ NS S3S2S1 + 1000]m16 = 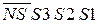 .
.
Через те, що за відсутності переповнення 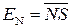 (ENNS дорівнює 01 або 10) різницю
(ENNS дорівнює 01 або 10) різницю 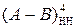 можна формувати за співвідношенням:
можна формувати за співвідношенням:

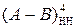 = EN S3S2S1,
= EN S3S2S1,
яке збігається з відповідним правилом (1.138) SMНН(А+В).
На завершення розглянемо типові приклади віднімання чисел у кодах з негативним нулем (рис.1.47).
Припустімо, що потрібно обчислити різницю 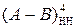 за таких аргументів: А = - 011; В = - 001. За цих умов на виходах SMНН(А-В) (рис.1.47) отримаємо:
за таких аргументів: А = - 011; В = - 001. За цих умов на виходах SMНН(А-В) (рис.1.47) отримаємо:

 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 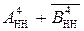 ]5 =
]5 =
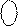

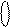


 = [ 0 100 +
= [ 0 100 + 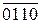 ]5 = ( 0 100 + 1 001)5 = 0 1 101;
]5 = ( 0 100 + 1 001)5 = 0 1 101;
EN = 0; NS = 1; S3S2S1 = 101;
ПП(А-В) = 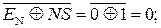
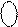

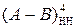 = EN S3S2S1 = 0 101 = (- 010)
= EN S3S2S1 = 0 101 = (- 010) 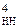 .
.
Розглянемо далі приклад із переповненням розрядної сітки SMНН(А-В) (рис. 1.47). Припустімо, що операнди суматора утворюють такі числа:
А = - 110; В = + 111. За цих аргументів числовий стан суматора визначається кодом:
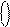



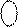


 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 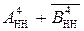 ]5 =[ 0 001 +
]5 =[ 0 001 + 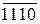 ]5 =
]5 =
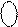 = [ 0 001 + 0 001]5 =[ 0 010]5 = 0 0 010,
= [ 0 001 + 0 001]5 =[ 0 010]5 = 0 0 010,
EN = 0; NS = 0;
ПП(А-В) = 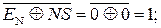
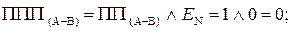
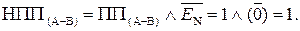
Таким чином, операція над числами призвела до негативного перепов-нення розрядної сітки суматора SMНН(А-В).
Вправи та запитання до розділу 1
1. За допомогою яких циклічних функцій (у формі подання зміщених чисел «за модулем») обчислюються чотирипозиційні машинні зображення чисел у доповняльних та оберних кодах? Вкажіть параметри відображення n-вимірних доповняльних та обернених кодів. Як здійснюється обчислення доповняльних та обернених кодів чисел за значень: -101110, +10101, -101, +101, -1011011.
2. Знайдіть найбільше та найменше значення змінної А, якщо її доповняльні і обернені коди зображаються 10-вимірним рядком біт. Обчисліть діапазон зміни аргументів для машинних кодів 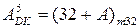 і
і 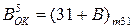 ,
,
де 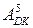 ,
, 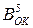 - відповідно доповняльний і обернений код змінних А і В за п’ятирозрядним форматом.
- відповідно доповняльний і обернений код змінних А і В за п’ятирозрядним форматом.
3. Доведіть справедливість співвідношення: (-100011) 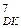 = (-100011)
= (-100011) 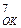 + 1.
+ 1.
4. Доведіть справедливість співвідношень:
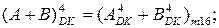
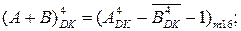
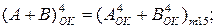
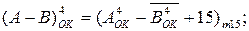
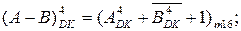
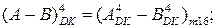
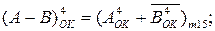
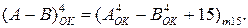
Знайдіть за вищеприведеними співвідношеннями суму і різницю операндів А і В за значень: А = -101, В = +001.
Запропонуйте прості структури арифметичних пристроїв, котрі викону-ють вищеприведені операції 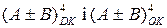 . За допомогою яких функ-цій можна виявити переповнення розрядної сітки у побудованих арифметик-них пристроях, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів
. За допомогою яких функ-цій можна виявити переповнення розрядної сітки у побудованих арифметик-них пристроях, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів 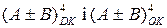 .
.
5. 
 За допомогою яких функцій обчислюються машинні зображення чисел з позитивним та негативним нулем? Вкажіть величину зміщення для
За допомогою яких функцій обчислюються машинні зображення чисел з позитивним та негативним нулем? Вкажіть величину зміщення для 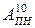 і
і 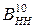 , де
, де 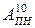 ,
, 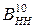 - машинні 10-вимірні зображення чисел А і В відповідно з позитивним і негативним нулем. Як здіснюється обчислення коду з позитивним і негативним нулем чисел за значень: - 011, + 010, - 1010, + 1101.
- машинні 10-вимірні зображення чисел А і В відповідно з позитивним і негативним нулем. Як здіснюється обчислення коду з позитивним і негативним нулем чисел за значень: - 011, + 010, - 1010, + 1101.
6. Знайдіть найбільше і найменше значення змінної А, якщо її зображення з позитивним і негативним нулем подається 8-вимірним рядком біт. Обчисліть діапазон зміни аргументів для машинних кодів 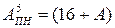 і
і 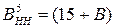 , де
, де 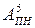 ,
, 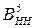 - відповідно комп’ютерні подання чисел А і В за п’ятирозрядним форматом у кодах з позитивним і негативним нулем.
- відповідно комп’ютерні подання чисел А і В за п’ятирозрядним форматом у кодах з позитивним і негативним нулем.
7. 
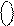
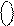 Доведіть справедливість співвідношень:
Доведіть справедливість співвідношень:
(+101) 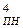 = 1 101; (- 101)
= 1 101; (- 101) 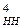 = 0 010; (- 101)
= 0 010; (- 101) 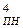 = 0 011.
= 0 011.
8. Доведіть справедливість співвідношень: 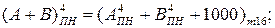
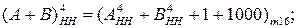
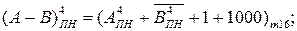
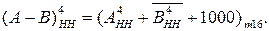
Знайдіть (А ± В) 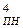 і (А ± В)
і (А ± В) 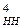 за таких значень операндів : А = + 011, В =- 001.
за таких значень операндів : А = + 011, В =- 001.
Запропонуйте прості структури арифметичних пристроїв, котрі обчис-люють (А ± В) 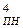 і (А ± В)
і (А ± В) 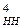 . За допомогою яких функцій у побудованих арифметичних пристроях можна виявити переповнення розрядної сітки, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів (А ± В)
. За допомогою яких функцій у побудованих арифметичних пристроях можна виявити переповнення розрядної сітки, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів (А ± В) 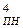 і (А ± В)
і (А ± В) 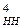 .
.
9. 
 Обгрунтуйте логічні правила перетворення прямого коду чисел
Обгрунтуйте логічні правила перетворення прямого коду чисел 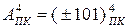 і
і 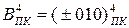 на інший машинний код того ж розміру (
на інший машинний код того ж розміру (  ,
, 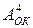 ,
, 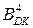 ,
, 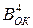 ,
, 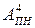 ,
, 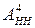 ,
, 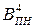 ,
, 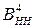 ).
).
10. 

 Нехай потрібно виконати додавання (за D=0) або віднімання (за D=1) чисел у прямих кодах:
Нехай потрібно виконати додавання (за D=0) або віднімання (за D=1) чисел у прямих кодах:
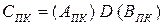 , де
, де 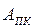 = NA MA,
= NA MA, 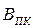 = NВ MВ,
= NВ MВ, 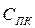 = NС MС; MA, MВ, MС – відповідно модулі (абсолютні значення) чисел А, В, С;
= NС MС; MA, MВ, MС – відповідно модулі (абсолютні значення) чисел А, В, С;
NA, NВ, NС – відповідно знакові розряди чисел А, В, С у прямих кодах.
Доведіть, що DM = NA  D
D  NВ, де DM – дія, котра повинна виконуватися над модулями прямих кодів чисел ( 0 - при додаванні модулів, 1- при відніманні модулів).
NВ, де DM – дія, котра повинна виконуватися над модулями прямих кодів чисел ( 0 - при додаванні модулів, 1- при відніманні модулів).
 Покажіть, що
Покажіть, що 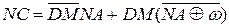 , де
, де
 1, якщо МА ≥ МВ;
1, якщо МА ≥ МВ;
0, якщо МВ >МА.
11. Доведіть, що за DM = 1
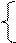
 S, якщо МА ≥ МВ;
S, якщо МА ≥ МВ;
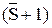 , якщо МВ >МА,
, якщо МВ >МА,
де S = (МА + 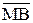 + 1)m16, МА=
+ 1)m16, МА= 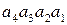 , МВ =
, МВ = 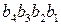 , МС =
, МС = 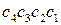 .
.
Запропонуйте просту структуру арифметичного пристрою для реалізації функції МС. Вкажіть змінну арифметичного пристрою, яка визначає ознаку відношення модулів
 1, при МА ≥ МВ;
1, при МА ≥ МВ;
0, при МВ >МА.
12. Покажіть, що за DM = 1
 (S+1), якщо МВ >МА;
(S+1), якщо МВ >МА;
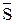 , якщо МА ≥ МВ.
, якщо МА ≥ МВ.
де S = ( 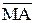 + МВ)m16, МА=
+ МВ)m16, МА= 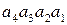 , МВ =
, МВ = 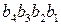 , МС =
, МС = 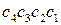 .
.
Запропонуйте просту структуру арифметичного пристрою для обчислення МС. Вкажіть змінну арифметичного пристрою, яка визначає ознаку відношення модулів
 1, при МА ≥ МВ;
1, при МА ≥ МВ;
0, при МВ >МА.
 13. Доведіть, що за DM = 0
13. Доведіть, що за DM = 0 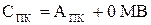 .
.
Найдіть залежності, які визначають ознаку переповнення розрядної сітки такого суматора.
 14. Покажіть, що за DM = 1
14. Покажіть, що за DM = 1
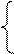

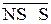 , якщо МА ≥ МВ;
, якщо МА ≥ МВ;
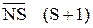 , якщо МВ >МА,
, якщо МВ >МА,
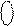
 де NS S =
де NS S = 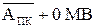 .
.
Запропонуйте просту структуру арифметичного пристрою для обчис-лення СПК. Найдіть формули і побудуйте логічну схему для визначення ознаки співвідношення модулів:
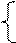
 1, якщо МА ≥ МВ;
1, якщо МА ≥ МВ;
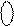
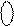 0, якщо МВ >МА.
0, якщо МВ >МА.
Хай АПК = 0 1011, ВПК = 0 1101.
 Знайдіть СПК =( АПК + ВПК) та ознаку ω. Який результат одержимо при АПК = 0 1101 і ВПК = 1 1011.
Знайдіть СПК =( АПК + ВПК) та ознаку ω. Який результат одержимо при АПК = 0 1101 і ВПК = 1 1011.
2. ТЕОРЕТИЧНІ ЗАСАДИ ТА СТРУКТУРА АРИФМЕТИЧНИХ ПРИСТРОЇВ ДЛЯ ВИКОНАННЯ ОПЕРАЦІЙ МНОЖЕННЯ ЦІЛИХ ЧИСЕЛ ІЗ ЗНАКОМ
2.1 Теоретичні засади та структура арифметичних пристроїв для множення цілих чисел у прямих кодах
Операція алгебричного множення чисел у прямих кодах зводиться до перетворення прямих кодів співмножників АПК і ВПК у прямий код добутку СПК:


 СПК = АПК * ВПК,
СПК = АПК * ВПК,
де АПК = NА МА, ВПК = NB MB, СПК = NC MC ;


 МА, MB, MC – відповідно модулі (цифрова частина) множеного, множника і добутку;
МА, MB, MC – відповідно модулі (цифрова частина) множеного, множника і добутку;
NА , NB , NC - відповідно знаковi розряди прямого коду співмножників і добутку.
Згідно з правилами алгебри знаковий розряд (NC) і модуль добутку (МС) визначаються виразами:
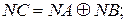 ( 2.1 )
( 2.1 )
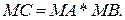 ( 2.2 )
( 2.2 )
Для п’ятирозрядних співмножників 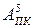 і
і 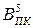 модулі операндів і до-бутку мають вигляд:
модулі операндів і до-бутку мають вигляд:
МА(4/1) =а4а3а2а1; МВ(4/1) = b4b3b2b1; MC(8/1)= c8c7c6c5c4c3c2c1,
де а4 …а1, b4 …b1, c8c7…c1 – відповідно двійкові цифри модулів співмножників і добутку.
Операція множення модулів чисел зводиться до множення модуля множеного МА на кожну цифру полінома множника МВ і підсумовування цих часткових добутків з урахуванням ваги кожної цифри множника:
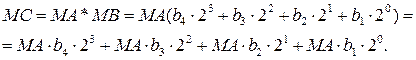
Залежно від способу реалізації виразу розрізняють чотири базових алгоритмiв множення (рис.2.1).
Пристрій множення чисел по алгоритму «А» (рис.2.1,а) реалізується за співвідношенням:


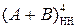 за таких аргументів: А = - 010; В = - 011. За цих умов числовий вираз стану суматора SM НН(А+В) (рис.1.46) визначається за формулою:
за таких аргументів: А = - 010; В = - 011. За цих умов числовий вираз стану суматора SM НН(А+В) (рис.1.46) визначається за формулою:
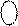
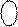

 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 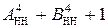 ]5 =
]5 =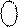 = [ 0 101 + 0 100 + 1]5 = (1010)5 = 0 1 010,
= [ 0 101 + 0 100 + 1]5 = (1010)5 = 0 1 010,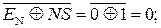


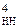 .
.


 Припустімо далі, що потрібно обчислити суму
Припустімо далі, що потрібно обчислити суму 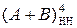 за таких аргументів: А = - 110; В = -101. За цих умов отримаємо: EN NS S3S2S1 = [
за таких аргументів: А = - 110; В = -101. За цих умов отримаємо: EN NS S3S2S1 = [ 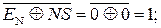
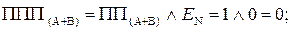
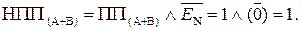
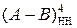 повинна обчислюватися за формулою:
повинна обчислюватися за формулою: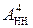 -
- 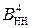 + 7 + 16)m16 =
+ 7 + 16)m16 =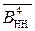 )m16 + 1000) m16, (1.139)
)m16 + 1000) m16, (1.139)
 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 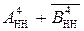 ]5 =
]5 = =15 + (9 ¸ 16) =
=15 + (9 ¸ 16) = 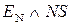 .
.

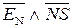 .
.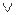 НПП(А-В) =
НПП(А-В) = 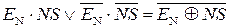 , (1.140)
, (1.140)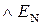 , НПП(А-В) = ПП(А-В)
, НПП(А-В) = ПП(А-В) 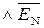 .
.
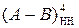 згідно з (1.139) формується за правилом:
згідно з (1.139) формується за правилом: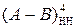 = [(EN NS S3S2S1)m16 + 1000]m16 =
= [(EN NS S3S2S1)m16 + 1000]m16 = = [ NS S3S2S1 + 1000]m16 =
= [ NS S3S2S1 + 1000]m16 = 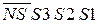 .
.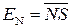 (ENNS дорівнює 01 або 10) різницю
(ENNS дорівнює 01 або 10) різницю 
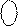
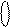
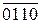 ]5 = ( 0 100 + 1 001)5 = 0 1 101;
]5 = ( 0 100 + 1 001)5 = 0 1 101;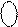
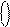

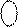
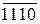 ]5 =
]5 =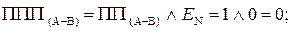
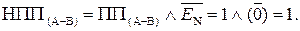
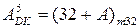 і
і 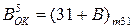 ,
,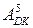 ,
, 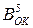 - відповідно доповняльний і обернений код змінних А і В за п’ятирозрядним форматом.
- відповідно доповняльний і обернений код змінних А і В за п’ятирозрядним форматом.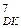 = (-100011)
= (-100011) 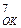 + 1.
+ 1.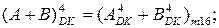
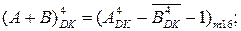
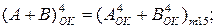
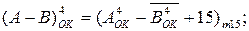
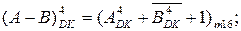
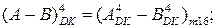
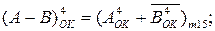
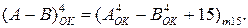
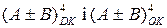 . За допомогою яких функ-цій можна виявити переповнення розрядної сітки у побудованих арифметик-них пристроях, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів
. За допомогою яких функ-цій можна виявити переповнення розрядної сітки у побудованих арифметик-них пристроях, тобто вихід результату (А ± В) за припустимі межі зміни аргументів числових кодів 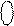
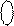
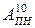 і
і 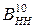 , де
, де 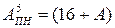 і
і 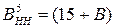 , де
, де 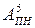 ,
, 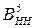 - відповідно комп’ютерні подання чисел А і В за п’ятирозрядним форматом у кодах з позитивним і негативним нулем.
- відповідно комп’ютерні подання чисел А і В за п’ятирозрядним форматом у кодах з позитивним і негативним нулем.
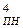 = 1 101; (- 101)
= 1 101; (- 101) 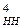 = 0 010; (- 101)
= 0 010; (- 101) 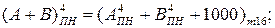
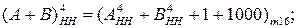
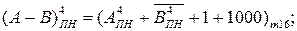
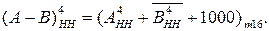
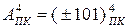 і
і 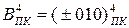 на інший машинний код того ж розміру (
на інший машинний код того ж розміру (  ,
, 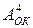 ,
, 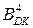 ,
, 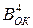 ,
, 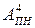 ,
, 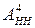 ,
, 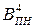 ,
, 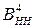 ).
).
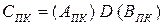 , де
, де 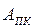 = NA MA,
= NA MA, 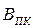 = NВ MВ,
= NВ MВ, 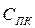 = NС MС; MA, MВ, MС – відповідно модулі (абсолютні значення) чисел А, В, С;
= NС MС; MA, MВ, MС – відповідно модулі (абсолютні значення) чисел А, В, С;  D
D 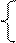 Покажіть, що
Покажіть, що 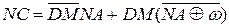 , де
, де 1, якщо МА ≥ МВ;
1, якщо МА ≥ МВ;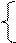
 S, якщо МА ≥ МВ;
S, якщо МА ≥ МВ;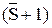 , якщо МВ >МА,
, якщо МВ >МА,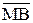 + 1)m16, МА=
+ 1)m16, МА= 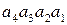 , МВ =
, МВ = 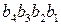 , МС =
, МС = 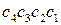 .
.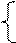
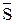 , якщо МА ≥ МВ.
, якщо МА ≥ МВ.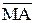 + МВ)m16, МА=
+ МВ)m16, МА= 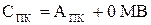 .
. 14. Покажіть, що за DM = 1
14. Покажіть, що за DM = 1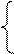
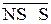 , якщо МА ≥ МВ;
, якщо МА ≥ МВ;
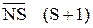 , якщо МВ >МА,
, якщо МВ >МА, де NS S =
де NS S = 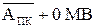 .
.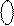


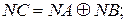 ( 2.1 )
( 2.1 )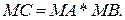 ( 2.2 )
( 2.2 )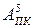 і
і 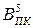 модулі операндів і до-бутку мають вигляд:
модулі операндів і до-бутку мають вигляд: