

 EN NS S3S2S1 = [16 – (МА + МВ)]5=[16 - (8 ¸ 1)]5=
EN NS S3S2S1 = [16 – (МА + МВ)]5=[16 - (8 ¸ 1)]5=

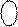
 = (8 ¸ 15)5 = 0 1 000 ¸ 0 1 111.
= (8 ¸ 15)5 = 0 1 000 ¸ 0 1 111.

 Тобто за відсутності негативного переповнення на виходах суматора (рис.1.44) формується код:
Тобто за відсутності негативного переповнення на виходах суматора (рис.1.44) формується код:
EN NS = 01.
Отже, згідно приведених міркувань при додаванні чисел одного знака переповнення розрядної сітки суматора з позитивним нулем (ПП(А+В)) потрібно обчислювати за формулою:
ПП(А+В) = ППП(А+В) + НПП(А+В) =
= 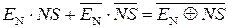 , (1.132)
, (1.132)
причому ППП(А+В) = ПП(А+В) × EN; НПП(А+В) = ПП(А+В) × 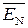 .
.
Остаточна сума чисел 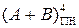 за відсутності переповнення згідно з (1.131) формується за правилом:
за відсутності переповнення згідно з (1.131) формується за правилом:



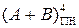 = (( EN NS S3S2S1)m16 + 1000)m16 =
= (( EN NS S3S2S1)m16 + 1000)m16 =
 = NS S3S2S1 + 1000)m16 =
= NS S3S2S1 + 1000)m16 = 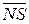 S3S2S1.
S3S2S1.
У зв’язку з тим, що за відсутності переповнення (за ознакою ПП = 0) на виходах суматора EN NS виникає код 10 або 01, тобто EN ≠ NS, остаточну суму (А + В)ПН можна формувати за правилом (рис.1.44):

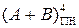 = EN S3S2S1, (1.133)
= EN S3S2S1, (1.133)
 де ЕN – визначення знака функції
де ЕN – визначення знака функції 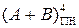 через вихідне перенесення суматора EN.
через вихідне перенесення суматора EN.
На завершення розглянемо типові приклади додавання чисел з позитивним нулем (рис.1.44).
Припустімо, що потрібно обчислити суму 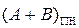 за таких аргументів: А = - 001; В = -101. За цих умов на виходах SMПН(А+В) (рис.1.44) отримаємо:
за таких аргументів: А = - 001; В = -101. За цих умов на виходах SMПН(А+В) (рис.1.44) отримаємо:
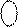

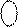
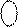

 EN NS S3S2S1 =
EN NS S3S2S1 = 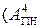 +
+ 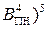 =( 0 111 + 0 010)5 = 0 1 010;
=( 0 111 + 0 010)5 = 0 1 010;
ЕN = 0; NS = 1; S3S2S1 = 010;
ПП(А+В) = 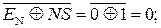


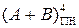 = EN S3S2S1 = 0 010 = (-110)
= EN S3S2S1 = 0 010 = (-110) 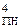 .
.
Припустімо далі, що потрібно обчислити у функцію (А+В)ПН за таких аргументів: А = - 110; В = -111. За цих умов отримаємо:


 EN NS S3S2S1 =
EN NS S3S2S1 = 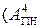 +
+ 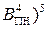 = ( 0 010 + 0 001)5 = 0 0 011;
= ( 0 010 + 0 001)5 = 0 0 011;
ПП(А+В) = 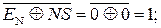
ППП(А+В) = ПП(А+В) 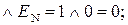
НПП(А+В) = ПП(А+В) 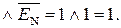
Таким чином, за цих аргументів виникає ознака НПП=1, тобто виникає переповнення розрядної сітки суматора SMПН(А+В).
Нехай далі операнди суматора SMПН(А+В) (рис.1.44) мають значення: А= + 110; В = +101.
За цих аргументів двійкові коди суматора та ознаки операції набувають таких значень:





 EN NS S3S2S1 =
EN NS S3S2S1 = 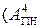 +
+ 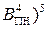 = ( 1 110 + 1 101)5 = 1 1 011;
= ( 1 110 + 1 101)5 = 1 1 011;
ПП(А+В) = 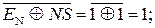
ППП(А+В) = ПП(А+В) 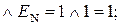
НПП(А+В) = ПП(А+В) 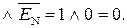
Таким чином, за цих значень аргументів виникає негативне перепов-нення розрядної сітки суматора SMПН(А+В).
Побудуємо тепер правила віднімання чисел з позитивним кодуванням нуля.
За алгоритмом визначення коду з позитивним нулем різниця чисел 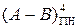 повинна обчислюватися за формулою:
повинна обчислюватися за формулою:
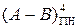 = 8 + (А - В).
= 8 + (А - В).
Для спрощення схеми формувача різниці чисел (А-В) 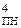 формулу перетворимо наступним чином:
формулу перетворимо наступним чином:
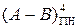 = (8 +А) - (8 + В) + 8 =
= (8 +А) - (8 + В) + 8 = 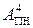 -
- 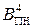 + 8 = = [
+ 8 = = [ 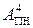 +(15 -
+(15 - 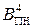 )+1+8 ]m16
)+1+8 ]m16 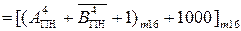 , (1.134)
, (1.134)
де 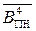 - інверсне значення коду
- інверсне значення коду 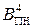 .
.
Через те, що аргументи функцій 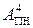 і
і 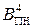 визначені у проміжку число-вої прямої між (-8) і (+7), функція
визначені у проміжку число-вої прямої між (-8) і (+7), функція 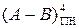 також існує у діапазоні від (-8) до (+7). З урахуванням такого обмеження, очевидно, позитивне переповнення функції
також існує у діапазоні від (-8) до (+7). З урахуванням такого обмеження, очевидно, позитивне переповнення функції 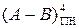 виникає у тому випадку, коли А = + МА і В = - МВ, тобто, коли (А - В) = (МА + МВ) і сумісно утворюють (МА+ МВ) = (8 ¸ 14). У цьому випадку повна п’ятирозрядна сума на виходах суматора (рис.1.45) складає код:
виникає у тому випадку, коли А = + МА і В = - МВ, тобто, коли (А - В) = (МА + МВ) і сумісно утворюють (МА+ МВ) = (8 ¸ 14). У цьому випадку повна п’ятирозрядна сума на виходах суматора (рис.1.45) складає код:

 EN NS S3S2S1 =
EN NS S3S2S1 = 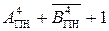 = (8 – МА) +15 - (8 - МВ) + 1 =
= (8 – МА) +15 - (8 - МВ) + 1 =
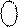
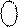

 = 16 + (МА + МВ) = 16 + (8 ¸ 14) = 24 ¸ 30 = 1 1 000 ¸ 1 1 110.
= 16 + (МА + МВ) = 16 + (8 ¸ 14) = 24 ¸ 30 = 1 1 000 ¸ 1 1 110.
Таким чином, за наявності ознаки ППП(А-В)= 1 маємо EN NS = 11, тобто функцію ППП(А-В) можна обчислювати за формулою:
ППП(А-В) = EN NS .
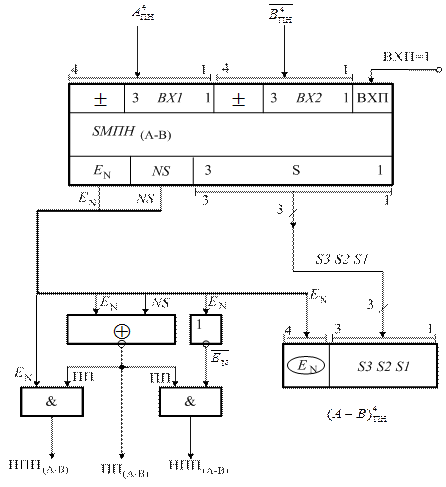
Рисунок 1.45 – Структурна схема суматора для віднімання
чисел у кодах з позитивним нулем(SMПН(А-В))
Негативне переповнення (НПП) функції 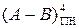 , очевидно, може виникати у тому випадку, коли А = - МА, В = + МВ, (А - В) = - (МА + МВ) = = (-9) ¸ (-16). Тоді на виходах суматора (
, очевидно, може виникати у тому випадку, коли А = - МА, В = + МВ, (А - В) = - (МА + МВ) = = (-9) ¸ (-16). Тоді на виходах суматора ( 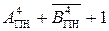 ) отримаємо двійковий рядок цифр (рис.1.45) :
) отримаємо двійковий рядок цифр (рис.1.45) :




 EN NS S3S2S1 = [16 – (МА + МВ)]5 =
EN NS S3S2S1 = [16 – (МА + МВ)]5 =
 = [16 + (9 ¸ 16)]5 = [7 ¸ 0]5 = 0 0 111 ¸ 0 0 000.
= [16 + (9 ¸ 16)]5 = [7 ¸ 0]5 = 0 0 111 ¸ 0 0 000.
Таким чином, за наявності ознаки НПП = 1 маємо EN NS = 00, тобто функцію НПП(А-В) можна визначити за формулою:
НПП(А-В) = 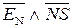 .
.
Із цих міркувань випливає:
ПП(А-В) = ППП(А-В) + НПП(А-В) = 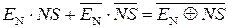 , (1.135)
, (1.135)
причому: ППП(А-В) = ПП(А-В) 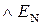 , НПП(А-В) = ПП(А-В)
, НПП(А-В) = ПП(А-В) 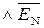 .
.
Таким чином, згідно з (1.132) і (1.135) ознака переповнення розрядної сітки при додаванні і відніманні чисел з позитивним нулем визначається еквівалентними булевими виразами, що спрощує побудову об’єднаного блока SM ПН(А+В) / SM ПН(А-В).
Остаточна різниця 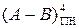 згідно з (1.134) формується за правилом :
згідно з (1.134) формується за правилом :


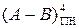 = [(EN NS S3S2S1)m16 + 1000]m16 =
= [(EN NS S3S2S1)m16 + 1000]m16 =
 = [ NS S3S2S1 + 1000]m16 =
= [ NS S3S2S1 + 1000]m16 = 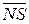
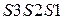 .
.
Через те, що за відсутності переповнення суматора 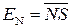 (ENNS дорівнює 01 або 10), різницю
(ENNS дорівнює 01 або 10), різницю 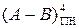 припустимо формувати за співвідно-шенням:
припустимо формувати за співвідно-шенням:

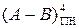 = ЕN S3S2S1,
= ЕN S3S2S1,
яка збігається з відповідним правилом (1.133).
На завершення розглянемо типові приклади віднімання чисел з позитивним нулем (рис.1.45).
Припустімо, що потрібно обчислити різницю 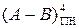 за таких аргументів: А=- 010; В = -110. За цих умов на виходах SMПН(А-В) (рис.1.45) отримаємо:
за таких аргументів: А=- 010; В = -110. За цих умов на виходах SMПН(А-В) (рис.1.45) отримаємо:
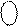



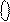


 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 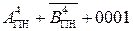 ]5 = [ 0 110 +
]5 = [ 0 110 + 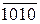 + 0001]5 =
+ 0001]5 =
= [ 0 110 + 0 101 + 0001]5 = 0 1 100;
NS = 1; EN = 0; S3S2S1 = 100; ПП(А-В) = 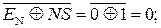


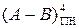 = ЕN S3S2S1 = 0 100 = (-100)
= ЕN S3S2S1 = 0 100 = (-100) 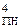 .
.
Припустімо далі, що потрібно обчислити різницю 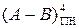 на виходах SMПН(А-В) (рис.1.45) за таких аргументів: А = + 011; В = -111. За цих умов отримаємо:
на виходах SMПН(А-В) (рис.1.45) за таких аргументів: А = + 011; В = -111. За цих умов отримаємо:



 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 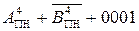 ]5 =[ 1 011 +
]5 =[ 1 011 + 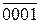 + 0001]5 =
+ 0001]5 =
 = [ 1 011 + 1 110 + 0001]5 = 265 = 1 1 010;
= [ 1 011 + 1 110 + 0001]5 = 265 = 1 1 010;
NS = 1; EN = 1; S3S2S1 = 010;
ПП(А-В) = 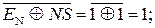
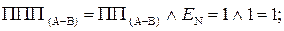
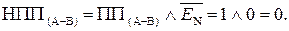
Таким чином, за цих аргументів виникає ознака ППП(А-В)=1 суматора SMПН(А-В).
Нехай операнди суматора SM ПН(А-В) мають значення: А=-101, В= +111. За цих аргументів на виходах SMПН(А-В) (рис.1.45) отримаємо:



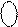

 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 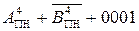 ]5 =[ 0 011 +
]5 =[ 0 011 + 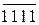 + 0001]5 =
+ 0001]5 =
= [ 0 011 + 0 000 + 0001]5 = ( 0 100)5 = 0 0 100;
NS = 0; EN = 0; S3S2S1 = 100;
ПП(А-В) = 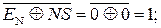
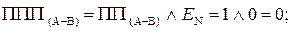
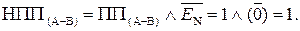
Таким чином, операція віднімання чисел за цих умов призвела до негативного переповнення SMПН(А-В).
1.6 Теоретичні засади та структура арифметичних пристроїв
для додавання і віднімання чисел у кодах з негативним нулем
Розглянемо операції додавання і віднімання чисел з негативним нулем 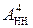 і
і 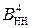 :
:

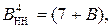
де 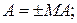
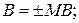 МА, МВ – відповідно модулі чисел А і В.
МА, МВ – відповідно модулі чисел А і В.
Зазначимо, що область значень чотирирозрядних функцій 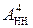 і
і 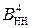 , утворюють множину кодів від 0000 до 1111, а область їх визначення – множину чисел від (-7) до (+8).
, утворюють множину кодів від 0000 до 1111, а область їх визначення – множину чисел від (-7) до (+8).
Побудуємо схеми для обчислення суми (А+В) чисел у кодах з негативним нулем.
Чотирирозрядний код суми чисел (А+В) з негативним нулем визначимо за загальним правилом:
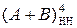 = 7 + (А + В).
= 7 + (А + В).
Звісно, що вираз можна подати також у вигляді:
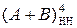 = (7 + А) + (7 + В) – 7 =
= (7 + А) + (7 + В) – 7 =
= ( 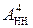 +
+ 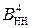 - 7 + 16)m16 =((
- 7 + 16)m16 =(( 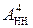 +
+ 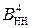 + 1)m16 + 1000) m16 (1.136)
+ 1)m16 + 1000) m16 (1.136)
Очевидно, що за допустимих значень аргументів А і В (які обмежені діапазоном числової осі від (-7) до (+8)) їх сума (А + В) може перевищувати область визначення аргумента функції 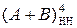 , яке також обмежене мно-жиною чисел від (-7) до (+8). Визначимо ознаки переповнення функції (1.136).
, яке також обмежене мно-жиною чисел від (-7) до (+8). Визначимо ознаки переповнення функції (1.136).
Передусім зазначимо, що за допустимих значень аргументів А і В їх сума (А+В) може змінюватись в межах від (+8) до (+16), тобто перевищувати область визначення функції 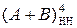 для додатних значень аргументу (А+В). За цих умов при обчисленні функції
для додатних значень аргументу (А+В). За цих умов при обчисленні функції 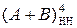 за формулою (1.136) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки.
за формулою (1.136) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки.
Негативне переповнення функції (1.136) (НПП(А+В)) виникає за тих допустимих від’ємних значень аргументів А і В, які сумісно формують множину чисел від (-8) до (-14). За цих умов при обчисленні 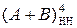 за алгоритмом (1.136) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)) розрядної сітки.
за алгоритмом (1.136) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)) розрядної сітки.
Для виявлення змінних обчислювача за формулою (1.136), які визначають ознаку переповнення розрядної сітки, розглянемо його роботу за умови, коли сума чисел (А + В) утворює ознаку позитивного або негативного переповнення функції 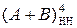 .
.

 У разі позитивного переповнення функції
У разі позитивного переповнення функції 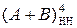 операнди
операнди 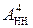 і
і 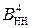 суматора (рис.1.46) являють собою зображення виключно додатних чисел А = + МА і В = + МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків
суматора (рис.1.46) являють собою зображення виключно додатних чисел А = + МА і В = + МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків 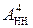 і
і 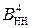 за позитивних операндів А і В набуває значення:
за позитивних операндів А і В набуває значення:

 EN NS S3S2S1 = [
EN NS S3S2S1 = [ 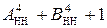 ]5 =
]5 =
=7 + А + 7 + В + 1 =7 + МА + 7 + МВ + 1 =15 + (МА + МВ).
 За умови позитивного переповнення суматора з негативним нулем, коли (А+В) = (9 ¸ 16), отримаємо:
За умови позитивного переповнення суматора з негативним нулем, коли (А+В) = (9 ¸ 16), отримаємо:
 EN NS S3S2S1 = 15 + (МА + МВ) =
EN NS S3S2S1 = 15 + (МА + МВ) =

 = 15 + (9 ¸ 16) = 24 ¸ 30 = 1 1 111 ¸ 1 1 110.
= 15 + (9 ¸ 16) = 24 ¸ 30 = 1 1 111 ¸ 1 1 110.
Таким чином, за умови позитивного переповнення SM НН маємо:
ППП(А+В) = 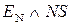 .
.

 При обчисленні суми від’ємних чисел А і В за формулою (1.136) може виникати негативне переповнення суматора (рис.1.46). У цьому випадку операнди А і В мають виключно від’ємні значення (А = - МА, В = - МВ), причому якщо ознака НПП(А+В) = 1, то сума модулів чисел (А+В) являє множину чисел від (-8) до (-14). Звідси отримаємо:
При обчисленні суми від’ємних чисел А і В за формулою (1.136) може виникати негативне переповнення суматора (рис.1.46). У цьому випадку операнди А і В мають виключно від’ємні значення (А = - МА, В = - МВ), причому якщо ознака НПП(А+В) = 1, то сума модулів чисел (А+В) являє множину чисел від (-8) до (-14). Звідси отримаємо:
EN NS S3S2S1 = (7 – МА) +(7 - МВ) + 1 =15 – (МА + МВ) =



 = 15 - (8 ¸ 14) = (7 ¸ 1)5 = 0 0 111 ¸ 0 0 001.
= 15 - (8 ¸ 14) = (7 ¸ 1)5 = 0 0 111 ¸ 0 0 001.
Таким чином, маємо:
НПП(А+В) = 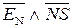 .
.
Отже, згідно з приведених міркувань при додаванні чисел одного знака переповнення суматор з негативним нулем (SMНН) потрібно обчислювати за формулою:
ПП(А+В) = ППП(А+В) 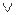 НПП(А+В) =
НПП(А+В) = 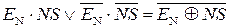 , (1.137)
, (1.137)
причому ППП(А+В) = ПП(А+В) 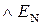 , НПП(А+В) = ПП(А+В)
, НПП(А+В) = ПП(А+В) 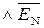 .
.
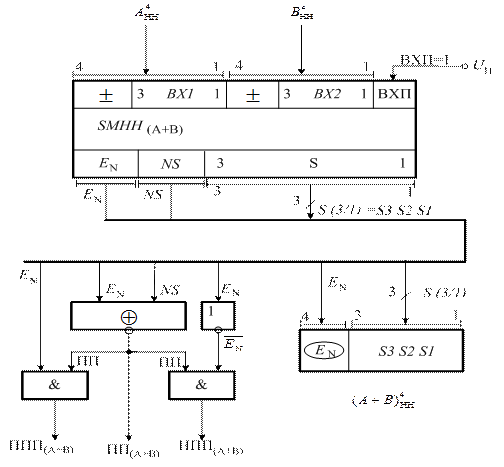
Рисунок 1.46 - Структурна схема для додавання
чисел у кодах з негативним нулем
Остаточна сума чисел 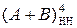 за відсутності переповнення згідно з (1.136) формується за правилом:
за відсутності переповнення згідно з (1.136) формується за правилом:



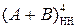 = [(EN NS S3S2S1)m16 + 1000]m16 =
= [(EN NS S3S2S1)m16 + 1000]m16 =
 = [ NS S3S2S1 + 1000]m16 =
= [ NS S3S2S1 + 1000]m16 = 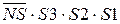 .
.
У зв’язку з тим, що за відсутності переповнення розрядної сітки (ознака ПП=0) на виводах суматора ЕN ¹ NS (ЕN NS дорівнює 01 або 10), остаточну суму (А+В)ПН, можна формувати за правилом:

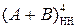 = EN S3S2S1, (1.138)
= EN S3S2S1, (1.138)
 де EN – визначення знакового розряду функції
де EN – визначення знакового розряду функції 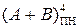 через вихідне перенесення суматора EN.
через вихідне перенесення суматора EN.




 EN NS S3S2S1 = [16 – (МА + МВ)]5=[16 - (8 ¸ 1)]5=
EN NS S3S2S1 = [16 – (МА + МВ)]5=[16 - (8 ¸ 1)]5=
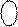

 Тобто за відсутності негативного переповнення на виходах суматора (рис.1.44) формується код:
Тобто за відсутності негативного переповнення на виходах суматора (рис.1.44) формується код: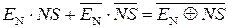 , (1.132)
, (1.132)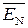 .
.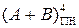 за відсутності переповнення згідно з (1.131) формується за правилом:
за відсутності переповнення згідно з (1.131) формується за правилом:

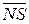 S3S2S1.
S3S2S1.
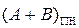 за таких аргументів: А = - 001; В = -101. За цих умов на виходах SMПН(А+В) (рис.1.44) отримаємо:
за таких аргументів: А = - 001; В = -101. За цих умов на виходах SMПН(А+В) (рис.1.44) отримаємо: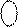

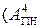 +
+ 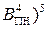 =( 0 111 + 0 010)5 = 0 1 010;
=( 0 111 + 0 010)5 = 0 1 010;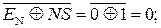

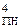 .
.
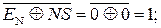
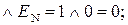
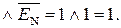
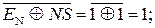
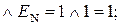
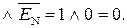
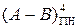 повинна обчислюватися за формулою:
повинна обчислюватися за формулою: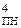 формулу перетворимо наступним чином:
формулу перетворимо наступним чином: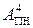 -
- 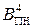 + 8 = = [
+ 8 = = [ 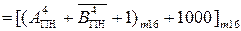 , (1.134)
, (1.134)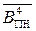 - інверсне значення коду
- інверсне значення коду 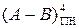 також існує у діапазоні від (-8) до (+7). З урахуванням такого обмеження, очевидно, позитивне переповнення функції
також існує у діапазоні від (-8) до (+7). З урахуванням такого обмеження, очевидно, позитивне переповнення функції 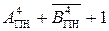 = (8 – МА) +15 - (8 - МВ) + 1 =
= (8 – МА) +15 - (8 - МВ) + 1 =

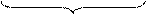


 = [16 + (9 ¸ 16)]5 = [7 ¸ 0]5 = 0 0 111 ¸ 0 0 000.
= [16 + (9 ¸ 16)]5 = [7 ¸ 0]5 = 0 0 111 ¸ 0 0 000.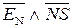 .
.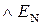 , НПП(А-В) = ПП(А-В)
, НПП(А-В) = ПП(А-В) 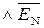 .
.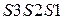 .
.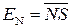 (ENNS дорівнює 01 або 10), різницю
(ENNS дорівнює 01 або 10), різницю 
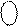
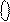

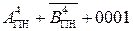 ]5 = [ 0 110 +
]5 = [ 0 110 + 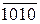 + 0001]5 =
+ 0001]5 =


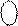
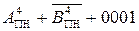 ]5 =[ 1 011 +
]5 =[ 1 011 + 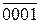 + 0001]5 =
+ 0001]5 =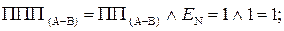
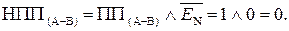
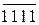 + 0001]5 =
+ 0001]5 =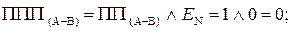
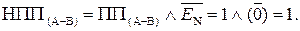
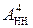 і
і 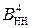 :
:
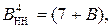
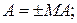
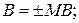 МА, МВ – відповідно модулі чисел А і В.
МА, МВ – відповідно модулі чисел А і В.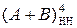 = 7 + (А + В).
= 7 + (А + В). У разі позитивного переповнення функції
У разі позитивного переповнення функції 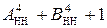 ]5 =
]5 =
 = 15 + (9 ¸ 16) = 24 ¸ 30 = 1 1 111 ¸ 1 1 110.
= 15 + (9 ¸ 16) = 24 ¸ 30 = 1 1 111 ¸ 1 1 110.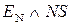 .
.
 При обчисленні суми від’ємних чисел А і В за формулою (1.136) може виникати негативне переповнення суматора (рис.1.46). У цьому випадку операнди А і В мають виключно від’ємні значення (А = - МА, В = - МВ), причому якщо ознака НПП(А+В) = 1, то сума модулів чисел (А+В) являє множину чисел від (-8) до (-14). Звідси отримаємо:
При обчисленні суми від’ємних чисел А і В за формулою (1.136) може виникати негативне переповнення суматора (рис.1.46). У цьому випадку операнди А і В мають виключно від’ємні значення (А = - МА, В = - МВ), причому якщо ознака НПП(А+В) = 1, то сума модулів чисел (А+В) являє множину чисел від (-8) до (-14). Звідси отримаємо:

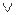 НПП(А+В) =
НПП(А+В) = 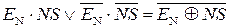 , (1.137)
, (1.137)

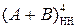 = [(EN NS S3S2S1)m16 + 1000]m16 =
= [(EN NS S3S2S1)m16 + 1000]m16 =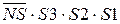 .
.
 де EN – визначення знакового розряду функції
де EN – визначення знакового розряду функції 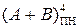 через вихідне перенесення суматора EN.
через вихідне перенесення суматора EN.