Звідси дістанемо:
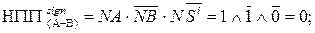
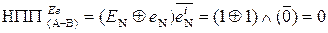 .
.
Припустімо далі, що різницю (А - В) потрібно обчислювати за таких значень аргументів: А = - 110; В = + 001. Очевидно, що у цьому випадку отримаємо:
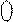






 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 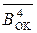 )5 = ( 1 001 +
)5 = ( 1 001 + 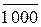 )5 =
)5 =
= ( 1 001 + 1 110)5 = 25 = 1 0 111; (EN=1, NS = 0, eN = 0);

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =

 = ( 0 111 + 0001) = 1 001; (
= ( 0 111 + 0001) = 1 001; ( 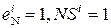 ) .
) .
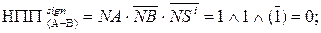
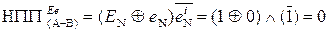 .
.
Розглянемо далі приклад, який ілюструє негативне переповнення розрядної сітки суматора обернених кодів (рис.1.40).
Нехай операнди чисел мають значення: А = - 110; В = + 111. За цих аргументів двійкові коди суматора ( 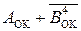 ) та ознаки операції набувають значень:
) та ознаки операції набувають значень:

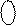
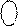

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 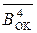 )5 = ( 1 001 +
)5 = ( 1 001 + 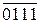 )5 =
)5 =


 = ( 1 001 + 1 000)5 = 17 = 1 0 001 (EN=1, NS = 0, eN = 0);
= ( 1 001 + 1 000)5 = 17 = 1 0 001 (EN=1, NS = 0, eN = 0);

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =

 = ( 0 001 + 0001) = 0 010 (
= ( 0 001 + 0001) = 0 010 ( 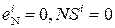 ) .
) .
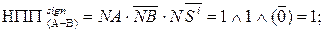
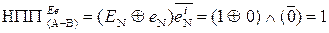 .
.
Таким чином, у даному випадку відбулося негативне переповнення розрядної сітки суматора ( рис.1.40).
Можлива структурна схема пристрою для додавання і віднімання чисел у обернених кодах подана на рис.1.41. Принцип роботи схеми полягає в тому, що спочатку за допомогою мультиплексора MUXB суматор (SM) пристрою налагоджується на виконання операції (1.112) або (1.121), а потім вихідний код SM перетворюється інкрементором (INC) в обернений код результату. Змінюючи кодову комбінацію на адресних входах мільтиплексора А1 і А0, можна отримати результат виду 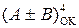 . Результат визначається як пра-вильний за відсутністю сигналу переповнення ПП розрядної сітки інкрементора (тобто за ознакою ПП = 0).
. Результат визначається як пра-вильний за відсутністю сигналу переповнення ПП розрядної сітки інкрементора (тобто за ознакою ПП = 0).
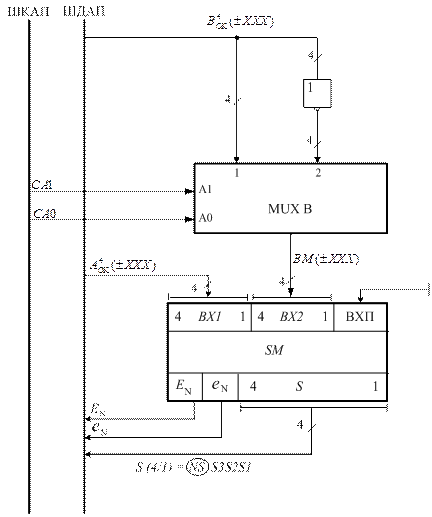
Рисунок 1.41,а – Модуль 1 арифметичного пристрою
для додавання і віднімання чисел у обернених кодах
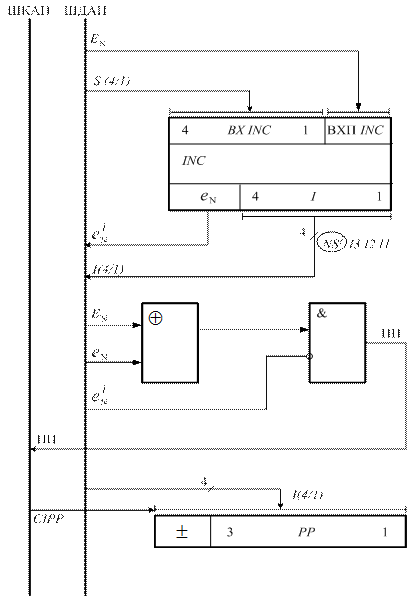
Рисунок 1.41,б – Модуль 2 арифметичного пристрою
для додавання і віднімання чисел у обернених кодах
Для спрощення виявлення переповнення розрядної сітки на практиці застосовується також модифікована форма обернених кодів (МОК), в яких знаковий розряд звичайного оберненого коду (1.110) дублюється.
Формально п’ятипозиційна модифікована форма чотирирозрядних обернених кодів операндів А і В визначається виразами:
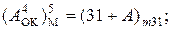
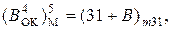
де  = (15 + А)m15,
= (15 + А)m15,  = (15 + В)m15 – відповідно звичайні чотири- розрядні обернені коди операндів А і В, обмежених у діапазоні числової прямої від (-7) до (+7);
= (15 + В)m15 – відповідно звичайні чотири- розрядні обернені коди операндів А і В, обмежених у діапазоні числової прямої від (-7) до (+7);
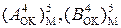 - модифікована форма обернених кодів А і В у п’ятипозиційному форматі з дублюванням знакових розрядів.
- модифікована форма обернених кодів А і В у п’ятипозиційному форматі з дублюванням знакових розрядів.
Модифікована форма оберненого кода суми чисел (А+В) обчислюється за співвідношенням:
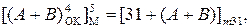
де 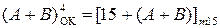 - звичайний обернений код суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7);
- звичайний обернений код суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7);
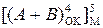 - модифікована форма оберненого коду суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7).
- модифікована форма оберненого коду суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7).
З урахуванням того, що (31)m31 = 0, на практиці для обчислення модифікованої форми оберненого коду суми чисел (А+В) використовується співвідношення:
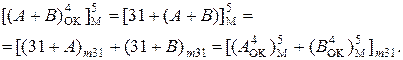 (1.128)
(1.128)
Можлива структурна схема для обчислення суми чисел (А+В) за алгоритмом (1.128) подана на рис.1.42.
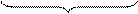
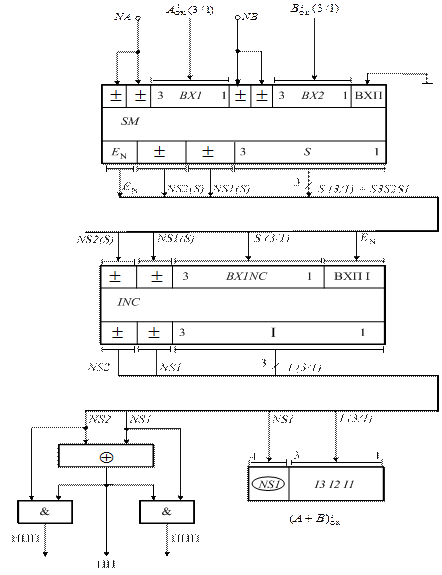
Рисунок 1.42 – Структурна схема арифметичного пристрою
для додавання чисел у модифікованих обернених кодах
Співвідношення (1.128) справедливо, якщо |A + B| ≤ 7, інакше в суматорах модифікованих кодів (рис.1.42) потрібно фіксувати переповнення розрядної сітки. За однакових знаків чотирирозрядних аргументів  і
і  (А=±МА≤ ±7, В=±МВ ≤ ±7) переповнення виникає за умови, коли сума (А+В)= =±(МА+МВ)= ± (8 ¸ 14). Згідно з (1.128) на виходах суматора модифікованих обернених кодів (SM МОК) у цьому випадку (тобто при ПП=1) формуються коди (рис.1.42):
(А=±МА≤ ±7, В=±МВ ≤ ±7) переповнення виникає за умови, коли сума (А+В)= =±(МА+МВ)= ± (8 ¸ 14). Згідно з (1.128) на виходах суматора модифікованих обернених кодів (SM МОК) у цьому випадку (тобто при ПП=1) формуються коди (рис.1.42):

 NS2 NS1 I3 I2 I1 =[
NS2 NS1 I3 I2 I1 =[ 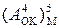 +
+ 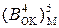 ]m31 =
]m31 =
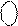
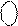
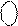
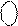 =
= 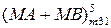 = (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.
= (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.

 NS2 NS1 I3 I2 I1 =[
NS2 NS1 I3 I2 I1 =[ 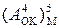 +
+ 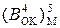 ]m31 =
]m31 =
= (31 – МА + 31 – МВ)m31 = [31 – (MA + MB)]m31 =
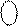 = [31 – (MA + MB)]m31 = [31 – [(-8) ¸ (-14)]]5 =
= [31 – (MA + MB)]m31 = [31 – [(-8) ¸ (-14)]]5 =
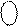
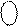
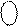 = 23 ¸ 17 = 1 0 111 ¸ 1 0 001.
= 23 ¸ 17 = 1 0 111 ¸ 1 0 001.


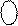 За коректних значень від’ємної суми |А+В| ≤ 7 (тобто за ознакою ПП=0) модифікована форма оберненого коду SM МОК (рис.1.42) відображає правильний код позитивної і негативної суми :
За коректних значень від’ємної суми |А+В| ≤ 7 (тобто за ознакою ПП=0) модифікована форма оберненого коду SM МОК (рис.1.42) відображає правильний код позитивної і негативної суми :
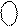
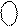
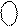 NS2 NS1 I3I2I1 = + (MA + MB) = (0 ¸ 7)= 0 0 000 ¸ 0 0 111;
NS2 NS1 I3I2I1 = + (MA + MB) = (0 ¸ 7)= 0 0 000 ¸ 0 0 111;

 NS2 NS1 I3I2I1 = 31 – (MA + MB) =
NS2 NS1 I3I2I1 = 31 – (MA + MB) =
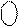
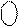
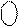
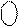 = 31 + [(-1) ¸ (-7)] = 30 ¸ 24 = 1 1 110 ¸ 1 1 000.
= 31 + [(-1) ¸ (-7)] = 30 ¸ 24 = 1 1 110 ¸ 1 1 000.
Узагальнюючи, маємо:
ППП = 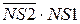 ; НПП =
; НПП = 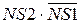 .
.
Таким чином, ознаку переповнення (ПП) суми чисел (А + В) можна обчислювати за формулою:
ПП = ППП 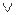 НПП =
НПП = 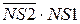
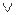
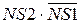 =
= 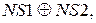 (1.129)
(1.129)
причому :
ППП = ПП 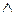 NS1; НПП = ПП
NS1; НПП = ПП 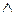 NS2.
NS2.
З урахуванням того, що (А – В) = А + (-В) і згідно з (1.128) справедливо:
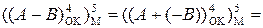
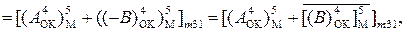 (1.130)
(1.130)
де 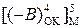 - машинне зображення чисел [-(В)] у модифікованій формі оберненого коду – інвертоване значення коду
- машинне зображення чисел [-(В)] у модифікованій формі оберненого коду – інвертоване значення коду 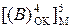 .
.
Отже, для обчислення правильної різниці чисел (А–В) у модифікованій формі оберненого коду досить на інформаційних входах блока підсумовуван-ня чисел (рис.1.42) змінити код 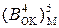 на його інвертоване значення
на його інвертоване значення 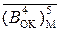 (рис.1.43). При цьому ознака переповнення в суматорі повинна визначатися при (А-В)=+(8¸14) і (А-В)=-(8¸14), тобто за співвідно-шенням (1.129).
(рис.1.43). При цьому ознака переповнення в суматорі повинна визначатися при (А-В)=+(8¸14) і (А-В)=-(8¸14), тобто за співвідно-шенням (1.129).
Для ілюстрації алгоритмів додавання і віднімання чисел на основі суматора модифікованих обернених кодів розглянемо типові приклади згаданих операцій.
Припустімо, що потрібно обчислити суму (А + В) за таких значень аргументів: А = - 010; В = - 001. За цих умов на виходах SMMOK (рис.1.42), отримаємо:







 NS2 NS1 I3 I2 I1 =[
NS2 NS1 I3 I2 I1 =[ 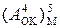 +
+ 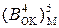 ]m31 =
]m31 =
=[ 1 1 101 + 1 1 110] m31 = 1 1 011;
ПП = 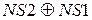 = 1
= 1  1 = 0.
1 = 0.
Розглянемо далі приклади, які ілюструють переповнення розрядної сітки.
Припустімо, що потрібно обчислити суму чисел (А + В) за таких значень аргументів: А = - 101; В = - 110. За цих умов на виходах SMМОК (рис.1.42) отримаємо:

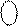





 NS2 NS1 I3 I2 I1 = [
NS2 NS1 I3 I2 I1 = [ 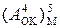 +
+ 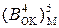 ]m31 =
]m31 =
=[ 1 1 010 + 1 1 001]m31 = 1 0 011;
ПП = 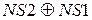 = 1
= 1  0 = 1;
0 = 1;
ППП = ПП 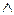 NS1 = 1
NS1 = 1 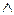 0 = 0;
0 = 0;
НПП = ПП 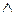 NS2 = 1
NS2 = 1 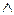 1 = 1.
1 = 1.
Таким чином, у цьому випадку виникає негативне переповнення суматора (рис.1.42).
Припустімо далі, що потрібно обчислити різницю чисел (А - В) за формулою (1.130) (рис.1.43).
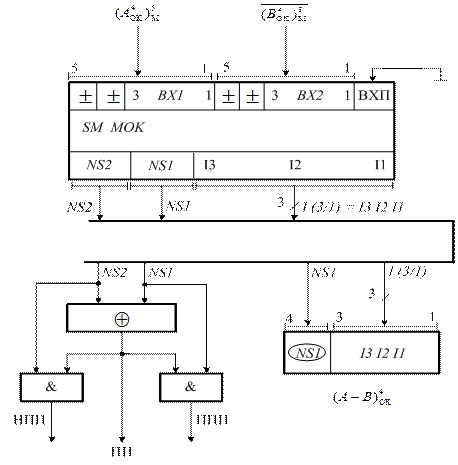
Рисунок 1.43 – Структурна схема арифметичного пристрою для
обчислення різниці чисел (А – В) у модифікованих обернених кодах
Нехай операнди мають значення: А = + 101; В = - 110. За цих аргументів на виходах пристрою для обчислення різниці чисел у модифікованій формі обернених кодів (рис.1.43) дістанемо:

 NS2 NS1 I3 I2 I1 = [
NS2 NS1 I3 I2 I1 = [ 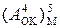 +
+ 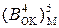 ]m31 =
]m31 =

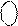
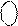
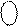
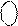

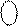

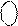
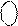 =[ 0 0 101+
=[ 0 0 101+ 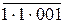 ]m31 = [ 0 0 101 + 0 0 110]m31 = 0 1 011;
]m31 = [ 0 0 101 + 0 0 110]m31 = 0 1 011;
ПП = 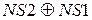 = 0
= 0  1 = 1;
1 = 1;
ППП = ПП 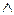 NS1 = 1
NS1 = 1 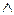 1 = 1;
1 = 1;
НПП = ПП 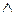 NS2 = 1
NS2 = 1 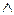 0 = 0.
0 = 0.
Отже, за цих аргументів в арифметичному пристрої для обчислення різниці чисел (рис.1.43) виникає позитивне переповнення розрядної сітки суматора.
1.5 Теоретичні засади та структура арифметичних пристроїв для додавання і віднімання чисел у кодах з позитивним нулем
Для ілюстрації основних функціональних особливостей лічби суми і різниці чисел у зміщених кодах з позитивним нулем розглянемо роботу чотирирозрядного пристрою. У такому пристрої машинні зображення операндів, наприклад А і В, у зміщених кодах з позитивним нулем згідно з (1.17) визначаються виразами:
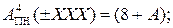
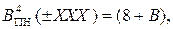
де 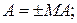
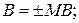 МА, МВ – відповідно модулі чисел А і В;
МА, МВ – відповідно модулі чисел А і В;
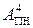 ,
, 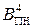 - відповідно зображення чисел А і В у кодах з позитивним нулем за чотирирозрядним форматом.
- відповідно зображення чисел А і В у кодах з позитивним нулем за чотирирозрядним форматом.
Побудуємо схеми для обчислення суми (А + В) з позитивним нулем.
Чотирирозрядний код суми (А + В) з позитивним нулем визначимо за загальним правилом (1.17):
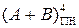 = 8 + (А + В).
= 8 + (А + В).
Звісно, що вираз можна представити також у вигляді:
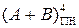 = (8 + А) + (8 + В) – 8 =
= (8 + А) + (8 + В) – 8 = 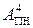 +
+ 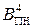 - 8.
- 8.
З урахуванням того, що (16)m16 = 0 справедливо:
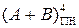 = [
= [ 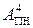 +
+ 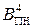 - 8 + 16]m16 =
- 8 + 16]m16 =
= [ 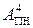 +
+ 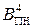 + 1000 ]m16 = [(
+ 1000 ]m16 = [( 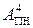 +
+ 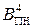 )m16 + 1000 ]m16 . (1.131)
)m16 + 1000 ]m16 . (1.131)
Очевидно, що за допустимих значень аргументів А і В (обмежених проміжком числової осі між (-8) і (+7)) їх сума (А + В) може перевищувати допустиме значення аргументу функції 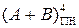 , яке також обмежене діапазоном чисел від (-8) до (+7). Визначимо ознаки переповнення функції (1.131).
, яке також обмежене діапазоном чисел від (-8) до (+7). Визначимо ознаки переповнення функції (1.131).
Передусім зазначимо, що за допустимих значень додатних аргументів А і В їх сума (А+В) може змінюватися в межах від (+8) до (+14), тобто перевищувати область визначення функції 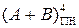 для додатних значень аргумента (А+В). За цих умов при обчисленні
для додатних значень аргумента (А+В). За цих умов при обчисленні 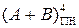 за алгоритмом (1.131) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки.
за алгоритмом (1.131) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки.
Негативне переповнення функції (1.131) (НПП(А+В)) виникає за тих допустимих від’ємних значень аргументів А і В, які сумісно формують множину чисел від (-9) до (-16). За цих умов при обчисленні 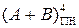 за формулою (1.131) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)) розрядної сітки.
за формулою (1.131) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)) розрядної сітки.
Для виявлення змінних обчислювача (1.131), які визначають ознаку переповнення розрядної сітки, розглянемо його роботу за умови, коли сума чисел (А + В) утворює позитивне переповнення функції 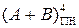 .
.
У разі позитивного переповнення (ознака ППП(А+В)=1) функції 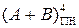 операнди
операнди 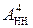 і
і 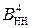 суматора (рис.1.44) являють зображення виключно додатних чисел А = +МА і В = +МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків
суматора (рис.1.44) являють зображення виключно додатних чисел А = +МА і В = +МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків 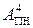 і
і 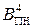 за позитивних операндів А і В набуває значення:
за позитивних операндів А і В набуває значення:



 EN NS S3S2S1= (
EN NS S3S2S1= ( 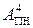 +
+ 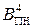 ) =
) =
=(8 + А + 8 + В) = 16 + МА + МВ =16 +( МА + МВ).
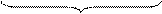
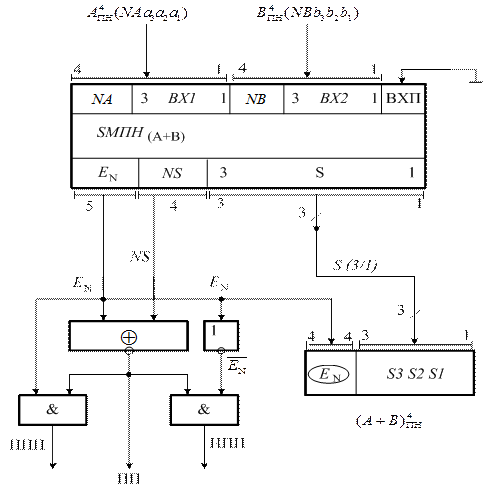
Рисунок 1.44 – Структурна схема суматора для обчислення
суми чисел у кодах з позитивним нулем(SMПН(А+В))
За умови позитивного переповнення суматора, коли (А+В) = (+8)¸(+14), отримаємо:





 EN NS S3S2S1 = 16 +( МА + МВ) =
EN NS S3S2S1 = 16 +( МА + МВ) =
= 16 + (8 ¸ 14) = 24 ¸ 30 = 1 1 000 ¸ 1 1 110.
Таким чином, за наявності позитивного переповнення SMПН (ознака ППП(А+В)=1), маємо:
ППП(А+В) = 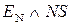 .
.

 Зазначимо, що у випадку, коли ознака ППП(А+В) = 0, тобто при (А+В) = = 0 ¸ (+7), п’ятирозрядна сума EN NS S3S2S1 на виходах суматора (SMПН) (рис.1.44) набуває значення:
Зазначимо, що у випадку, коли ознака ППП(А+В) = 0, тобто при (А+В) = = 0 ¸ (+7), п’ятирозрядна сума EN NS S3S2S1 на виходах суматора (SMПН) (рис.1.44) набуває значення:

 EN NS S3S2S1 = 16 +( МА + МВ) =
EN NS S3S2S1 = 16 +( МА + МВ) =

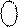
 = 16 + (0 ¸ 7) = 16 ¸ 23 = 1 0 000 ¸ 1 0 111.
= 16 + (0 ¸ 7) = 16 ¸ 23 = 1 0 000 ¸ 1 0 111.

 Отже, за відсутності позитивного переповнення на виводах суматора (рис.1.44) формуються коди:
Отже, за відсутності позитивного переповнення на виводах суматора (рис.1.44) формуються коди:
EN NS = 10.

 При обчисленні суми від’ємних чисел А і В за алгоритмом (1.131) може виникати негативне переповнення (НПП(А+В)) суматора (рис.1.44). У цьому випадку операнди А і В мають виключно від’ємні значення (А= -МА, В= -МВ), причому за ознакою НПП(А+В)= 1 сума чисел (A + B) являє множину чисел від (-9) до (-16). Звідси випливає:
При обчисленні суми від’ємних чисел А і В за алгоритмом (1.131) може виникати негативне переповнення (НПП(А+В)) суматора (рис.1.44). У цьому випадку операнди А і В мають виключно від’ємні значення (А= -МА, В= -МВ), причому за ознакою НПП(А+В)= 1 сума чисел (A + B) являє множину чисел від (-9) до (-16). Звідси випливає:
 EN NS S3S2S1 = (8 – МА) +(8 - МВ) =16 – (МА + МВ)=
EN NS S3S2S1 = (8 – МА) +(8 - МВ) =16 – (МА + МВ)=


 = 16 + (9 ¸ 16) = 7 ¸ 0 = 0 0 111 ¸ 0 0 000.
= 16 + (9 ¸ 16) = 7 ¸ 0 = 0 0 111 ¸ 0 0 000.
Отже, за умови, коли ознака НПП(А+В)= 1, ЕN = 0 і NS = 0. Звідси маємо:
НПП(А+В) = 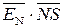 .
.
Зазначимо, що, якщо сума від’ємних чисел (А < 0 і B < 0) являє допустиму множину від’ємних аргументів функції (1.131), тобто (МА + МВ) =8 ¸ 1, то:


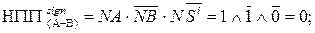
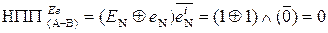 .
.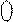



 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 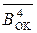 )5 = ( 1 001 +
)5 = ( 1 001 + 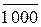 )5 =
)5 =
 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN = = ( 0 111 + 0001) = 1 001; (
= ( 0 111 + 0001) = 1 001; ( 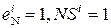 ) .
) .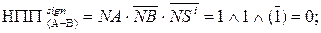
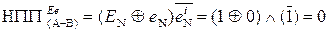 .
.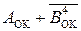 ) та ознаки операції набувають значень:
) та ознаки операції набувають значень:
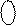
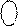

 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 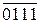 )5 =
)5 =
 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =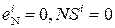 ) .
) .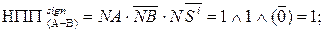
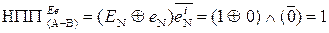 .
.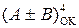 . Результат визначається як пра-вильний за відсутністю сигналу переповнення ПП розрядної сітки інкрементора (тобто за ознакою ПП = 0).
. Результат визначається як пра-вильний за відсутністю сигналу переповнення ПП розрядної сітки інкрементора (тобто за ознакою ПП = 0).

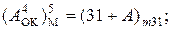
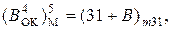
 = (15 + В)m15 – відповідно звичайні чотири- розрядні обернені коди операндів А і В, обмежених у діапазоні числової прямої від (-7) до (+7);
= (15 + В)m15 – відповідно звичайні чотири- розрядні обернені коди операндів А і В, обмежених у діапазоні числової прямої від (-7) до (+7);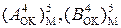 - модифікована форма обернених кодів А і В у п’ятипозиційному форматі з дублюванням знакових розрядів.
- модифікована форма обернених кодів А і В у п’ятипозиційному форматі з дублюванням знакових розрядів.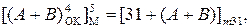
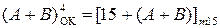 - звичайний обернений код суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7);
- звичайний обернений код суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7);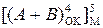 - модифікована форма оберненого коду суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7).
- модифікована форма оберненого коду суми чисел (А+В), обмеженої проміжком числової осі між (-7) і (+7).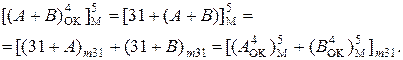 (1.128)
(1.128)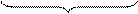


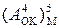 +
+ 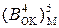 ]m31 =
]m31 =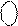
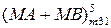 = (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.
= (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.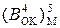 ]m31 =
]m31 = = [31 – (MA + MB)]m31 = [31 – [(-8) ¸ (-14)]]5 =
= [31 – (MA + MB)]m31 = [31 – [(-8) ¸ (-14)]]5 =

 За коректних значень від’ємної суми |А+В| ≤ 7 (тобто за ознакою ПП=0) модифікована форма оберненого коду SM МОК (рис.1.42) відображає правильний код позитивної і негативної суми :
За коректних значень від’ємної суми |А+В| ≤ 7 (тобто за ознакою ПП=0) модифікована форма оберненого коду SM МОК (рис.1.42) відображає правильний код позитивної і негативної суми :
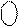
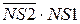 ; НПП =
; НПП = 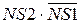 .
.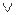 НПП =
НПП = 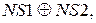 (1.129)
(1.129)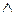 NS1; НПП = ПП
NS1; НПП = ПП 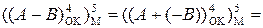
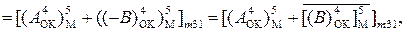 (1.130)
(1.130)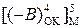 - машинне зображення чисел [-(В)] у модифікованій формі оберненого коду – інвертоване значення коду
- машинне зображення чисел [-(В)] у модифікованій формі оберненого коду – інвертоване значення коду 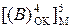 .
.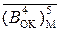 (рис.1.43). При цьому ознака переповнення в суматорі повинна визначатися при (А-В)=+(8¸14) і (А-В)=-(8¸14), тобто за співвідно-шенням (1.129).
(рис.1.43). При цьому ознака переповнення в суматорі повинна визначатися при (А-В)=+(8¸14) і (А-В)=-(8¸14), тобто за співвідно-шенням (1.129).
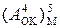 +
+ 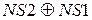 = 1
= 1  1 = 0.
1 = 0.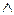 NS1 = 1
NS1 = 1 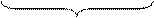

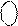
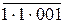 ]m31 = [ 0 0 101 + 0 0 110]m31 = 0 1 011;
]m31 = [ 0 0 101 + 0 0 110]m31 = 0 1 011;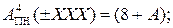
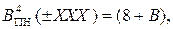
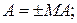
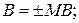 МА, МВ – відповідно модулі чисел А і В;
МА, МВ – відповідно модулі чисел А і В;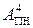 ,
, 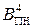 - відповідно зображення чисел А і В у кодах з позитивним нулем за чотирирозрядним форматом.
- відповідно зображення чисел А і В у кодах з позитивним нулем за чотирирозрядним форматом.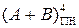 = 8 + (А + В).
= 8 + (А + В).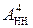 і
і 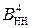 суматора (рис.1.44) являють зображення виключно додатних чисел А = +МА і В = +МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків
суматора (рис.1.44) являють зображення виключно додатних чисел А = +МА і В = +МВ, тому повна п’ятирозрядна сума EN NS S3S2S1 доданків 




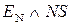 .
.

 = 16 + (0 ¸ 7) = 16 ¸ 23 = 1 0 000 ¸ 1 0 111.
= 16 + (0 ¸ 7) = 16 ¸ 23 = 1 0 000 ¸ 1 0 111.
 При обчисленні суми від’ємних чисел А і В за алгоритмом (1.131) може виникати негативне переповнення (НПП(А+В)) суматора (рис.1.44). У цьому випадку операнди А і В мають виключно від’ємні значення (А= -МА, В= -МВ), причому за ознакою НПП(А+В)= 1 сума чисел (A + B) являє множину чисел від (-9) до (-16). Звідси випливає:
При обчисленні суми від’ємних чисел А і В за алгоритмом (1.131) може виникати негативне переповнення (НПП(А+В)) суматора (рис.1.44). У цьому випадку операнди А і В мають виключно від’ємні значення (А= -МА, В= -МВ), причому за ознакою НПП(А+В)= 1 сума чисел (A + B) являє множину чисел від (-9) до (-16). Звідси випливає: EN NS S3S2S1 = (8 – МА) +(8 - МВ) =16 – (МА + МВ)=
EN NS S3S2S1 = (8 – МА) +(8 - МВ) =16 – (МА + МВ)=
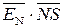 .
.