NA = 0; NB = 0; NS = 1; eN = 1; EN = 0; 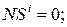
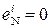 .
.
Зазначимо, що у випадку, коли ознака ППП(А+В) = 0, при додаванні додатних чисел А і В сума модулів (МА + МВ) змінюється в межах від 0 до 7 і на виводах суматора формується рядок двійкових цифр:


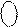


 (
( 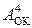 +
+  ) = EN NS S3S2S1 = 0 0 000 ¸ 0 0 111 .
) = EN NS S3S2S1 = 0 0 000 ¸ 0 0 111 .
Отже, змінні суматора знакових розрядів NA і NB (рис.1.39) за коректних значень оберненого коду суми (А + В) мають значення:
NA = 0; NB = 0; NS = 0; 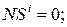 EN = 0; eN = 0;
EN = 0; eN = 0; 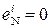 . (1.114)
. (1.114)
Згідно з цих міркувань ознаку позитивного переповнення суматора обернених кодів потрібно обчислювати за булевими формулами:
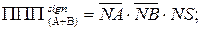 (1.115)
(1.115)
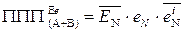 . (1.116)
. (1.116)
За алгоритмом (1.112) при обчисленні суми від’ємних чисел А і В може виникати також негативне переповнення (НПП(А+В)) суматора (рис.1.39). У цьому випадку операнди А і В мають виключно від’ємні значення, тобто А=(-МА)і В=(-МВ), причому за ознакою НПП(А+В) = 1 сума (МА+МВ) являє множину чисел від (- 8) до (- 14). Звідси дістанемо:


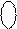

 EN NS S3S2S1 =
EN NS S3S2S1 =  +
+  = (15 – МА) + (15 – МВ) =
= (15 – МА) + (15 – МВ) =
 =30 – (МА + МВ) =30 – (8 ¸ 14) = 22 ¸ 16 = 1 0 110 ¸ 1 0 000.
=30 – (МА + МВ) =30 – (8 ¸ 14) = 22 ¸ 16 = 1 0 110 ¸ 1 0 000.
Таким чином, за умови, коли ознака НПП(А+В)=1, змінні суматора знакових розрядів SMN складають двійковий набір:
NA = 1; NB = 1; NS = 0; EN = 1; eN = 0; 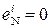
У випадку, коли ознака НПП(А+В)= 0 (при А<0 і В<0) і (А+В) = (-6)¸ (-1) повна сума (  +
+  )m15 складає рядок двійкових цифр:
)m15 складає рядок двійкових цифр:

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =
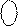

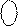
 =[(15 – МА) + (15 – МВ)]5 = [30 – (МА + МВ)]5 =
=[(15 – МА) + (15 – МВ)]5 = [30 – (МА + МВ)]5 =
=[30 – (6 ¸ 1)]5 = (24 ¸ 29)5 = 1 1 000 ¸ 1 1 101;




 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =
 = ( 1 000+ 0001) ¸ ( 1 101 + 0001) = 1 001 ¸ 1 110.
= ( 1 000+ 0001) ¸ ( 1 101 + 0001) = 1 001 ¸ 1 110.
Таким чином, за умови, коли ознака НПП(А+В)= 0 (при А < 0 і В < 0) і (А+В) = (-6)¸ (-1) змінні SMN і SMNi (рис.1.39) формують двійковий набір:
NA = 1; NB = 1; NS = 1; 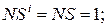 EN = 1; eN = 1;
EN = 1; eN = 1; 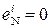 .
.
У випадку, коли ознака НПП(А+В)=0 і (А+В)= -7 при А<0 і В<0, функція 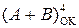 утворює рядок двійкових цифр (рис.1.39):
утворює рядок двійкових цифр (рис.1.39):



 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =
= [30 – (МА + МВ)]5 = [30 – 7]5 = 23 = 1 0 111;


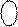
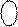 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =
= 0 111 + 0001 = 1 000.
Узагальнюючи можна зазначити, що за ознакою НПП(А+В) = 0 і (А+В) = -7 змінні SMN і (SMN)i (рис. 1.39) мають значення:
NA = 1; NB = 1; NS = 0; 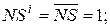 EN = 1; eN = 0;
EN = 1; eN = 0; 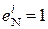 .
.
Таким чином, у загальному випадку ознака негативного переповнення розрядної сітки суматора обернених кодів (рис.1.39) повинна обчислюватися за допомогою однієї із формул:
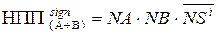 , (1.117)
, (1.117)
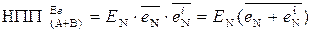 . (1.118)
. (1.118)
Отже, при додаванні чисел одного знаку переповнення суматора обернених кодів (ПП(А+В)) згідно з (1.115 ¸ 1.118) можна здійснювати за допомогою однієї з формул:
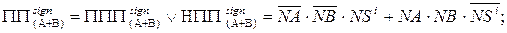 (1.119)
(1.119)
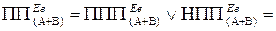
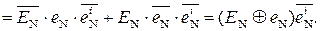 (1.120)
(1.120)
На завершення розглянемо типові приклади додавання чисел у обернених кодах (рис.1.39).
Нехай потрібно обчислити обернений код суми 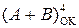 за таких зна-чень аргументів А=-001 і В= - 011. За цих умов на виходах SMOK (рис.1.39) отримаємо:
за таких зна-чень аргументів А=-001 і В= - 011. За цих умов на виходах SMOK (рис.1.39) отримаємо:
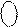

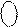
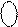

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 = [( 1 110 + 1 100] = 1 1 010 (eN = 1);
)5 = [( 1 110 + 1 100] = 1 1 010 (eN = 1);
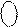
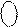

 NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 1 010 + 0001)5 = 1 011 (
NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 1 010 + 0001)5 = 1 011 ( 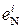 = 0).
= 0).
Звідси дістанемо:
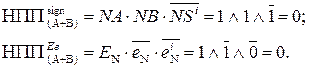
Припустімо далі, що потрібно обчислити суму (А + В) за таких аргументів: А = - 010; В = - 101. Очевидно, що у цьому випадку будуть справедливі такі визначення (рис.1.39):

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =




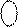 = [( 1 101 + 1 010] = 1 0 111 (eN = 0);
= [( 1 101 + 1 010] = 1 0 111 (eN = 0);
 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =
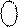
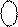 = ( 0 111 + 0001) = 1 000 (
= ( 0 111 + 0001) = 1 000 ( 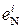 = 1);
= 1);
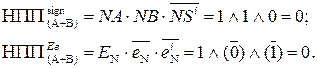
Розглянемо далі приклад, що ілюструє негативне переповнення розрядної сітки суматора при додаванні від’ємних чисел.
Нехай операнди суматора мають значення А = - 110 і В = - 111.
За цих аргументів двійкові коди обернених кодів суматора (рис.1.39) та ознаки операції набувають таких значень:


 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =


 = [( 1 001 + 1 000]5 = 1 0 001 (eN = 0);
= [( 1 001 + 1 000]5 = 1 0 001 (eN = 0);

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =
 = ( 0 001 + 0001) = 0 010 (
= ( 0 001 + 0001) = 0 010 ( 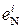 = 0);
= 0);
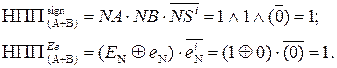
 Таким чином, у цьому разі маємо ознаку НПП(А+В) =1 і (
Таким чином, у цьому разі маємо ознаку НПП(А+В) =1 і (  +
+  )m15 = = 0 010 ¹
)m15 = = 0 010 ¹ 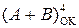 , тобто довжина суми (А + В) перевищує розрядну сітку суматора обернених кодів (рис.1.39).
, тобто довжина суми (А + В) перевищує розрядну сітку суматора обернених кодів (рис.1.39).
Розглянемо тепер правила віднімання чисел у обернених кодах.
Згідно з загальним правилом обчислення оберненого коду різниця чисел 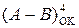 повинна визначатися за формулою:
повинна визначатися за формулою:
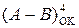 = [15 + (A - B)]m15.
= [15 + (A - B)]m15.
Для спрощення схеми формувача різниці чисел у обернених кодах формула звичайно перетворюється наступним чином:
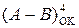 = (15 + А – (15 + В) + 15)m15 =
= (15 + А – (15 + В) + 15)m15 =
= [(15 + A)m15 + 15 – (15 + B)m15]m15 =
= (  + 15 -
+ 15 -  )m15 = (
)m15 = (  +
+ 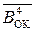 )m15 , (1.121)
)m15 , (1.121)
де  ,
,  - відповідно зображення обернених кодів чисел А і В за чотирипозиційним форматом.
- відповідно зображення обернених кодів чисел А і В за чотирипозиційним форматом.
Через те, що аргументи функцій  і
і  визначені у діапазоні чис-лової прямої від (-7) до (+7), функція
визначені у діапазоні чис-лової прямої від (-7) до (+7), функція 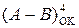 також існує у проміжку між (-7) і (+7). Тоді, очевидно, позитивне переповнення функції
також існує у проміжку між (-7) і (+7). Тоді, очевидно, позитивне переповнення функції 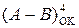 виникає у тому випадку, коли А=+МА, В= - МВ, (А - В) = (МА+МВ) і сумісно (МА+МВ)=(8 ¸ 14). У цьому випадку повна сума (
виникає у тому випадку, коли А=+МА, В= - МВ, (А - В) = (МА+МВ) і сумісно (МА+МВ)=(8 ¸ 14). У цьому випадку повна сума (  +
+ 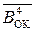 ) складає п’ятипозиційний код (рис.1.40):
) складає п’ятипозиційний код (рис.1.40):

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 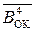 )5 =
)5 =
= (МА + 15 -  )5 = (МА +15 – (15 – МВ))5 =
)5 = (МА +15 – (15 – МВ))5 =



 = (МА + МВ)5 = (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.
= (МА + МВ)5 = (8 ¸ 14)5 = 0 1 000 ¸ 0 1 110.
Таким чином, за наявності ознаки ППП(А-В) = 1 змінні SMN і (SMN)i (рис. 1.40) мають значення:
NA = 0; 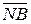 = 0; NS = 1;
= 0; NS = 1; 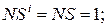 EN = 0; eN = 1;
EN = 0; eN = 1; 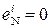 .
.
Якщо при А > 0 і B < 0 (A – B) = (0) ¸(+7), тобто (МА + МВ) =(0) ¸ (7) і ознака ППП(А-В) = 0, повна сума складає код:

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =
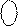

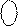
 = (МА + МВ)5 = 0 0 000 ¸ 0 0 111.
= (МА + МВ)5 = 0 0 000 ¸ 0 0 111.
Отже, за умови, коли ознака ППП(А-В) = 0, змінні SMN і (SMN)i (рис.1.40) мають значення:
NA = 0; 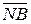 = 0; NS = 0;
= 0; NS = 0; 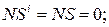 EN = 0; eN = 0;
EN = 0; eN = 0; 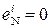 .
.
Виходячи з цих міркувань, маємо наступні способи фіксування позитивного переповнення суматора при відніманні чисел у обернених кодах (рис.1.40):
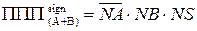 ; (1.122)
; (1.122)
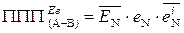 (1.123)
(1.123)
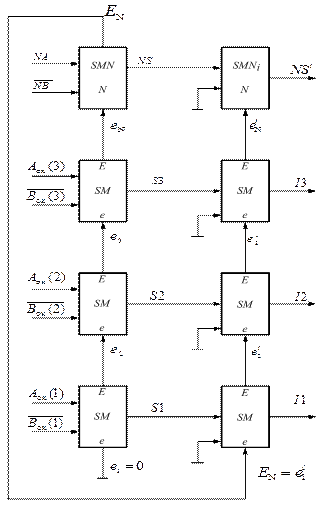
Рисунок 1.40 – Структурна схема суматора для віднімання чисел у обернених кодах
Негативне переповнення функції 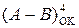 виникає у тому випадку, коли А=-МА, В = + МВ, (А - В)=-( МА + МВ) і сумісно (МА + МВ) утворюють множину чисел від 8 до 14. У цьому випадку повна сума (
виникає у тому випадку, коли А=-МА, В = + МВ, (А - В)=-( МА + МВ) і сумісно (МА + МВ) утворюють множину чисел від 8 до 14. У цьому випадку повна сума (  +
+ 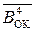 ) складає код (рис.1.40):
) складає код (рис.1.40):

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 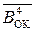 )5 =
)5 =
= [(15 – MA) + 15 – MB]5 = [30 - (МА + МВ)]5 =


 = [30 – (8 ¸ 14)]5 = (22¸16)5 = 1 0 110 ¸ 1 0 000;
= [30 – (8 ¸ 14)]5 = (22¸16)5 = 1 0 110 ¸ 1 0 000;


 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =


 = ( 0 110 + 0001) ¸ 0 001 + 0001) = 0 111 ¸ 0 010.
= ( 0 110 + 0001) ¸ 0 001 + 0001) = 0 111 ¸ 0 010.
Таким чином, за ознакою НПП(А-В) = 1 змінні SMN і (SMN)i (рис. 1.40) мають значення:
NA = 1; 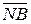 = 1(NB =0); NS = 0; eN = 0;
= 1(NB =0); NS = 0; eN = 0;
EN = 1; 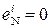 ;
; 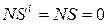 .
.
Якщо при А < 0 і B > 0 (A – B) = (-1) ¸(-6), тобто за (МА + МВ) = 0 ¸ 6 і ознака НПП(А-В) = 0, повна сума функції 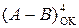 складає код (1.40):
складає код (1.40):

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 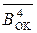 )5 = [(15 – MA) + 15 – MB]5 =
)5 = [(15 – MA) + 15 – MB]5 =

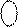 = [30 - (МА + МВ)]5 = [30 – (1 ¸ 6)]5 = (29 ¸ 24)5 =
= [30 - (МА + МВ)]5 = [30 – (1 ¸ 6)]5 = (29 ¸ 24)5 =

 = 1 1 101 ¸ 1 1 000;
= 1 1 101 ¸ 1 1 000;



 NS i I3 I2 I1 = NS S3S2S1 + 000EN = NS S3S2S1 + 0001 =
NS i I3 I2 I1 = NS S3S2S1 + 000EN = NS S3S2S1 + 0001 =
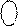
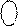
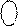 =( 1 101 + 0001) ¸ ( 1 000 + 0001) = 1 110 ¸ 1 001.
=( 1 101 + 0001) ¸ ( 1 000 + 0001) = 1 110 ¸ 1 001.
Таким чином, за умови, коли (А – В) = (-1) ¸ (-6) і ознака НПП(А-В) = 0, змінні SMN і (SMN)i (рис. 1.40) утворюють двійковий набір:
NA = 1; 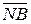 = 1 (NB = 0);
= 1 (NB = 0); 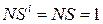 ;
;
NS = 1; EN = 1; eN = 1; 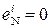 .
.
У випадку, коли (А – В) = -7, повна п’ятирозрядна сума (  +
+  ) складає код (рис.1.40):
) складає код (рис.1.40):



 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =
)5 =
= [30 - (МА + МВ)]5 = [30 – 7]5 = (23)5 = 1 0 111;



 NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 0 111 + 0001) = 1 000 .
NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 0 111 + 0001) = 1 000 .
Отже, якщо (А – В) = -7 і ознака НПП(А-В) = 0, змінні SMN і (SMN)i (рис. 1.40) мають значення:
NA = 1; 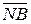 = 1 (NB = 0);
= 1 (NB = 0); 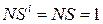 ; NS = 0; EN = 1; eN = 0;
; NS = 0; EN = 1; eN = 0; 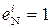 .
.
Узагальнюючі зазначимо, що негативне переповнення функції 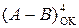 можна обчислювати за допомогою формул:
можна обчислювати за допомогою формул:
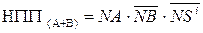 ; (1.124)
; (1.124)
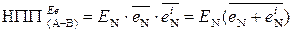 . (1.125)
. (1.125)
 Таким чином, згідно з (1.122) ¸ (1.125) переповнення функції
Таким чином, згідно з (1.122) ¸ (1.125) переповнення функції 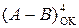 можна здійснювати за допомогою формул:
можна здійснювати за допомогою формул:
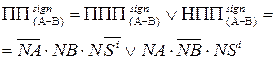
 (1.126)
(1.126)
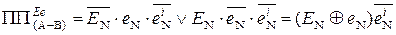 (1.127)
(1.127)
На завершення зазначимо, що згідно з формулами (1.120) і (1.127):
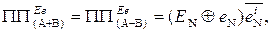
тобто формула для визначення ознаки ПП суматора інваріантна до знака операції, тому залежність (1.127) вважається найпростішим апаратним способом фіксації переповнення розрядної сітки у пристроях для додавання і віднімання чисел у обернених кодах.
Для ілюстрації алгоритмів віднімання чисел із використанням їх обернених кодів розглянемо типові приклади.
Припустімо, що потрібно обчислити різницю чисел за таких значень аргументів: А=-110; В=-111. За цих умов ( 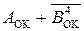 ) (рис.1.40) визначається співвідношенням:
) (рис.1.40) визначається співвідношенням:
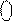
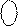
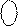
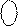

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 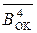 )5 =( 1 001 +
)5 =( 1 001 + 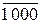 )5 =
)5 =

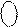 = ( 1 001 + 0 111)5 = 16 = 1 0 000 (EN=1, NS = 0, eN = 1);
= ( 1 001 + 0 111)5 = 16 = 1 0 000 (EN=1, NS = 0, eN = 1);

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =

 = ( 0 000 + 0001) = 0 001 (
= ( 0 000 + 0001) = 0 001 ( 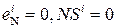 ) .
) .


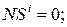
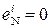 .
.

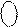

 (
( 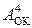 +
+  ) = EN NS S3S2S1 = 0 0 000 ¸ 0 0 111 .
) = EN NS S3S2S1 = 0 0 000 ¸ 0 0 111 .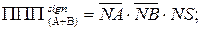 (1.115)
(1.115)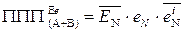 . (1.116)
. (1.116)

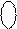
 +
+  =30 – (МА + МВ) =30 – (8 ¸ 14) = 22 ¸ 16 = 1 0 110 ¸ 1 0 000.
=30 – (МА + МВ) =30 – (8 ¸ 14) = 22 ¸ 16 = 1 0 110 ¸ 1 0 000.
 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 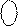

 =[(15 – МА) + (15 – МВ)]5 = [30 – (МА + МВ)]5 =
=[(15 – МА) + (15 – МВ)]5 = [30 – (МА + МВ)]5 =

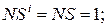 EN = 1; eN = 1;
EN = 1; eN = 1; 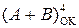 утворює рядок двійкових цифр (рис.1.39):
утворює рядок двійкових цифр (рис.1.39):
 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 

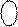
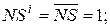 EN = 1; eN = 0;
EN = 1; eN = 0; 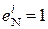 .
.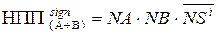 , (1.117)
, (1.117)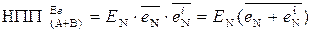 . (1.118)
. (1.118)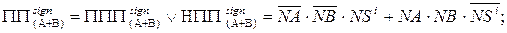 (1.119)
(1.119)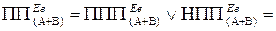
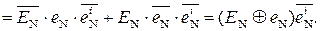 (1.120)
(1.120)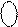

 NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 1 010 + 0001)5 = 1 011 (
NS i I3 I2 I1 = NS S3S2S1 + 000EN = ( 1 010 + 0001)5 = 1 011 ( 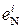 = 0).
= 0).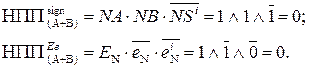
 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 

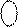 = [( 1 101 + 1 010] = 1 0 111 (eN = 0);
= [( 1 101 + 1 010] = 1 0 111 (eN = 0); NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =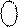
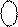 = ( 0 111 + 0001) = 1 000 (
= ( 0 111 + 0001) = 1 000 ( 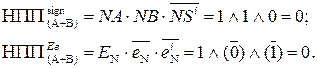

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =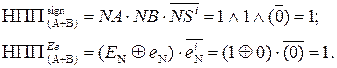
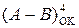 повинна визначатися за формулою:
повинна визначатися за формулою: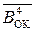 )m15 , (1.121)
)m15 , (1.121)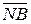 = 0; NS = 1;
= 0; NS = 1; 

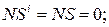 EN = 0; eN = 0;
EN = 0; eN = 0; 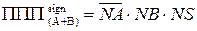 ; (1.122)
; (1.122)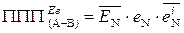 (1.123)
(1.123)

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =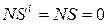 .
.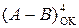 складає код (1.40):
складає код (1.40):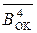 )5 = [(15 – MA) + 15 – MB]5 =
)5 = [(15 – MA) + 15 – MB]5 =
 NS i I3 I2 I1 = NS S3S2S1 + 000EN = NS S3S2S1 + 0001 =
NS i I3 I2 I1 = NS S3S2S1 + 000EN = NS S3S2S1 + 0001 =
 ;
; .
.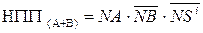 ; (1.124)
; (1.124)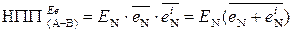 . (1.125)
. (1.125) Таким чином, згідно з (1.122) ¸ (1.125) переповнення функції
Таким чином, згідно з (1.122) ¸ (1.125) переповнення функції 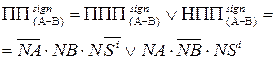
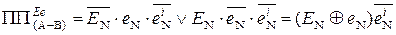 (1.127)
(1.127)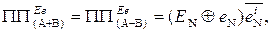
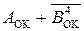 ) (рис.1.40) визначається співвідношенням:
) (рис.1.40) визначається співвідношенням: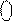

 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 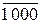 )5 =
)5 =

 NS i I3 I2 I1 = NS S3S2S1 + 000EN =
NS i I3 I2 I1 = NS S3S2S1 + 000EN =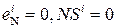 ) .
) .