Рисунок 1.36 – Структурна модель віднімального
пристрою чисел у доповняльних кодах
Таблиця 1.5 - Визначення ознаки ППП функції 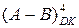

За цієї умови на виводах операційного суматора функції (1.85) формуються коди (  = (16 – МА),
= (16 – МА),  = МА ):
= МА ):

 EN NS S(3/1) = (
EN NS S(3/1) = (  +
+ 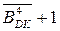 ) =
) =
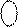

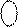 =16 – МА + 16 – МВ = 32 – (МА + МВ) =
=16 – МА + 16 – МВ = 32 – (МА + МВ) =
 =32 – [(-16) ¸ (-9)] = 16 ¸ 23 = 1 0 000 ¸ 1 0 111,
=32 – [(-16) ¸ (-9)] = 16 ¸ 23 = 1 0 000 ¸ 1 0 111,
тобто за умови, коли ознака НПП(А – В) = 1, маємо:
NA = 1; 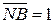 (NB = 0); NS = 0; EN = 1; eN = 0. ( 1.92 )
(NB = 0); NS = 0; EN = 1; eN = 0. ( 1.92 )
За відсутності переповнення функції (1.87) (ознака НПП(А–В)=0) різниця чисел (А – В) = (-8) ¸ (-1). Отже, на виводах операційного суматора функції (1.85) у цьому випадку формуються наступні коди повної суми (рис.1.35):


 EN NS S(3/1) = (
EN NS S(3/1) = (  +
+ 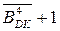 )5 = 32 – (МА + МВ) =
)5 = 32 – (МА + МВ) =

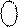
 = 32 – [(-8) ¸ (-1)] = 24 ¸ 31 = 1 1 000 ¸ 1 1 111,
= 32 – [(-8) ¸ (-1)] = 24 ¸ 31 = 1 1 000 ¸ 1 1 111,
тобто за умови, коли НПП(А – В) = 0, маємо:
NA = 1; 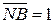 (NB = 0); NS = 1; EN = 1; eN = 1. ( 1.93 )
(NB = 0); NS = 1; EN = 1; eN = 1. ( 1.93 )
Співвідношення (1.92), (1.93) являють собою повну таблицю істинності функції НПП(А – В) (табл. 1.6). Звідкіль дістанемо:
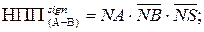
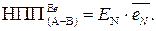 ( 1.94 )
( 1.94 )
Таким чином, при відніманні чисел у доповняльних кодах ознаку переповнення ПП(А–В) функції 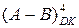 згідно з (1.88), (1.91) потрібно фіксувати за допомогою одного із булевих виразів:
згідно з (1.88), (1.91) потрібно фіксувати за допомогою одного із булевих виразів:
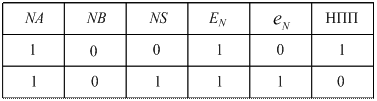
Таблиця 1.6 - Визначення ознаки НПП функції 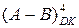
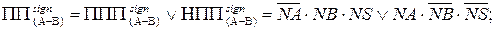 ( 1.95 )
( 1.95 )
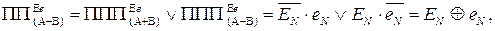 ( 1.96 )
( 1.96 )
причому:
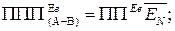 ( 1.97 )
( 1.97 )
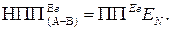 ( 1.98 )
( 1.98 )
Таким чином, із співвідношень (1.84 – 1.86), (1.96) – (1.98) випливає, що як при додаванні, так і при відніманні доповняльних кодів чисел справед-ливі такі визначення:
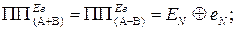 ( 1.99 )
( 1.99 )
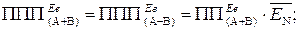 (1.100)
(1.100)
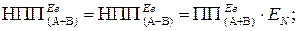 (1.101)
(1.101)
Розглянемо типові приклади віднімання чисел у доповняльних кодах.
Припустімо, що потрібно обчислити різницю чисел (А – В) за таких значень аргументів: А = - 011; В = - 010.
За цих умов згідно з (1.81) отримаємо:

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 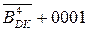 )5 =
)5 =

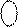 =( 1 101 +
=( 1 101 + 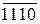 + 0001)5 = ( 1 101 + 0 001 + 0001)5 =
+ 0001)5 = ( 1 101 + 0 001 + 0001)5 =

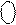 = (15)5 = 0 1 111 ( NS = 1, EN = 0, eN = 0 ).
= (15)5 = 0 1 111 ( NS = 1, EN = 0, eN = 0 ).
Звідки дістанемо:
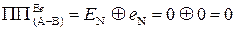 ;
;



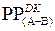 =
= 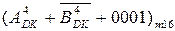 = ( 0 1 111)m16 = 1 111.
= ( 0 1 111)m16 = 1 111.
Розглянемо далі приклад, що ілюструє переповнення розрядної сітки пристрою при відніманні чисел у доповняльних кодах.
Припустімо, що потрібно знайти різницю чисел (А – В) за значень аргументів: А = - 110; В = +111.
За цих умов двійкові коди та ознаки операції 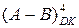 набувають значень:
набувають значень:

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+ 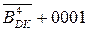 )5 =
)5 =
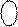
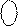
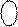
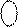 =( 1 010 +
=( 1 010 + 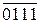 + 0001)5 = ( 1 010 + 1 000 + 0001)5 =
+ 0001)5 = ( 1 010 + 1 000 + 0001)5 =
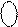
 = 19 = 1 0 011 (EN = 1, NS = 0, eN = 0 );
= 19 = 1 0 011 (EN = 1, NS = 0, eN = 0 );
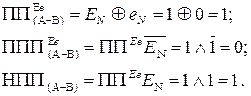
Отже, у цьому випадку виникає негативне переповнення розрядної сітки суматора.
Структурна схема чотирирозрядного суматора для виконання операції додавання (ADD) або віднімання (SUB) чисел у доповняльних кодах (DK) подана на рис.1.37. Функціональна схема являє собою композицію мульти-плексора MUXB і двійкового суматора. Мультиплексор у схемі використо-вується для налагоджування обчислювача на виконання операції 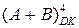 або
або 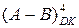 відповідно за сигналами керування CADD чи CSUB. За відсут-ності переповнення правильний результат формується на виводах S суматора.
відповідно за сигналами керування CADD чи CSUB. За відсут-ності переповнення правильний результат формується на виводах S суматора.
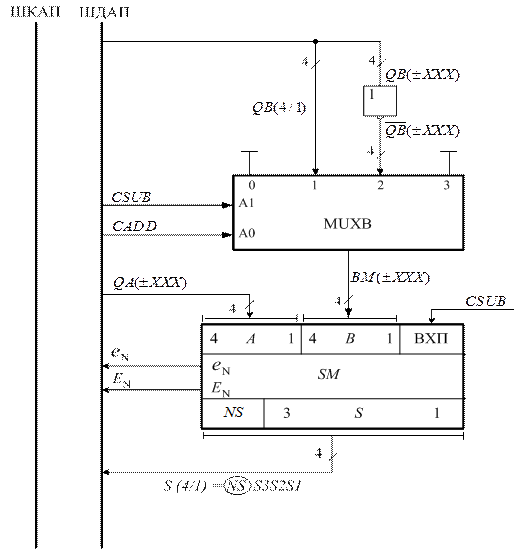
Рисунок 1.37 – Схема операційного суматора для
додавання і віднімання чисел у доповняльних кодах
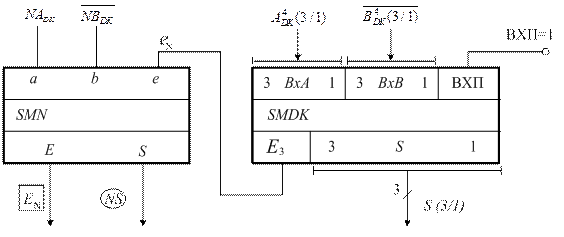
На завершення зазначимо, що для спрощення виявлення ознаки пере-повнення суматора при додаванні і відніманні чисел у доповняльних кодах може застосовуватися модифікована форма доповняльних кодів (МDК). Можливий варіант такої схеми подано на рис.1.38.
Передусім розглянемо роботу суматора з модифікованою формою доповняльного коду при додаванні додатних чисел А і В.
У цьому разі  = МА і
= МА і  = МВ, тому МDK буде визначатися за фор-мулою (рис.1.38):
= МВ, тому МDK буде визначатися за фор-мулою (рис.1.38):
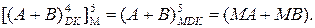
Рисунок 1.38 – Структурна схема арифметичного пристрою для
додавання і віднімання чисел у модифікованих доповняльних кодах
За умови, коли А + В ≤ +7, тобто за ознакою ППП(А+В)= 0, отримаємо:




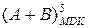 = NS2 NS1 S(3/1) = 0 0 000 ¸ 0 0 111. (1.102)
= NS2 NS1 S(3/1) = 0 0 000 ¸ 0 0 111. (1.102)
Якщо ознака ППП(А+В)= 1, тобто коли А + В =(+8) ¸ (+14), рядок двійкових цифр на виводах SMMDK відповідає множині чисел:
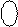
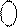
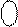


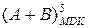 = NS2 NS1 S(3/1) = 0 1 000 ¸ 0 1 110 (8÷14). (1.103)
= NS2 NS1 S(3/1) = 0 1 000 ¸ 0 1 110 (8÷14). (1.103)
У разі додавання від’ємних чисел на входах SMMDK згідно з визначенням MDK формуються коди: (  )М = 32 – МА і (
)М = 32 – МА і (  )М = 32 – МВ (рис.1.38). На виводах SMMDK повна сума при цьому формується за співвідношенням:
)М = 32 – МВ (рис.1.38). На виводах SMMDK повна сума при цьому формується за співвідношенням:
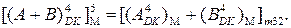 (1.104)
(1.104)
Отже, у випадку коли ознака НПП(А+В) = 0, тобто за умови коли (-1)≥(А + В) ≥ (-8), на виводах SMMDK формується двійковий код (рис.1.38):
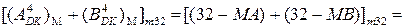
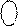
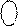
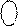
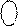 = 32 – (МА + МВ) = 31 ¸ 24 = 1 1 111 ¸ 1 1 000. (1.105)
= 32 – (МА + МВ) = 31 ¸ 24 = 1 1 111 ¸ 1 1 000. (1.105)
За наявності ознаки НПП(А+В) =1, тобто за умови, коли -16 ≤(А + В) ≥ -9, справедливі такі визначення:




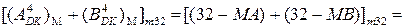
= 32 – (МА + МВ) = 16 ¸ 23 = 1 0 000 ¸ 1 0 111. (1.106)
Віднімання чисел (А - В) у SMMDK виконується звичайним способом обробки доповняльних кодів з урахуванням п’ятирозрядного формату суматора ( рис.1.38):
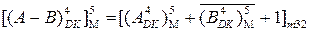 .
.
Очевидно, що результат операції може бути як позитивним, так і негативним у залежності від знаків чисел.
Якщо різниця чисел (А-В) додатна і формує множину чисел (+0) ¸ (+7), то ознака ППП(А+В)=0 і двійкові коди на виводах SM MDK визначаються формулою (1.102) (NS2=NS1=00). У випадку, коли додатна різниця формує множину чисел (МА + МВ) = (+8) ¸ (+14), очевидно, результат на виводах суматора MDK буде визначатися формулою (1.103) і перевищує довжину розрядної сітки суматора.
З цих міркувань випливає, що як при додаванні, так і при відніманні чисел виявлення ознаки позитивного переповнення розрядної сітки резуль-тату 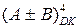 потрібно виконувати за еквівалентною формулою:
потрібно виконувати за еквівалентною формулою:
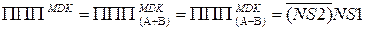 . (1.107)
. (1.107)
Якщо різниця чисел (А - В) від’ємна і формує множину чисел (-8) ¸ (-1), то ознака НПП(А-В) = 0 і двійкові коди на виводах SMMDK визначаються фор-мулою (1.104). У випадку, коли від’ємна різниця формує множину чисел [- (МА + МВ)] = (-9) ¸ (-16), то, очевидно, результат на виходах SMMDK визначається формулою (1.105) і перевищує область визначення функції 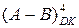 , тобто у цьому разі необхідно створювати ознаку НПП(А-В) = 1.
, тобто у цьому разі необхідно створювати ознаку НПП(А-В) = 1.
Таким чином, як при додаванні, так і при відніманні чисел виявлення ознаки негативного переповнення виразу 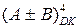 потрібно оцінювати за формулою:
потрібно оцінювати за формулою:
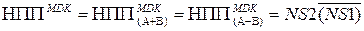 . (1.108)
. (1.108)
Із співвідношень (1.107) і (1.108) випливає, що у загальному випадку переповнення розрядної сітки доповняльного коду результату 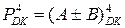 повинно мати активне значення за умови (рис.1.38) :
повинно мати активне значення за умови (рис.1.38) :

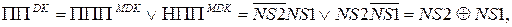 (1.109)
(1.109)
де ППDK – ознака переповнення розрядної сітки регістру доповняльного коду результату.
1.4 Теоретичні засади та структура арифметичних пристроїв
для додавання і віднімання чисел у обернених кодах
Для ілюстрації основних функціональних особливостей лічби суми і різниці чисел у обернених кодах розглянемо роботу чотирирозрядного пристрою.
У такому пристрої машинні зображення операндів, наприклад А і В, у обернених кодах згідно з (1.10) визначаються виразами:
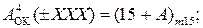
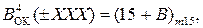 (1.110)
(1.110)
де А = ±МА; В = ±МВ; МА, МВ – відповідно модулі чисел А і В, які обмежені проміжком числової осі між (-7) і (+7);
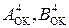 - відповідно обернені коди операндів А і В за чотири- розрядним форматом.
- відповідно обернені коди операндів А і В за чотири- розрядним форматом.
Побудуємо схеми для обчислення суми чисел ( А+В) 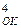 із використан-ням обернених кодів операндів
із використан-ням обернених кодів операндів 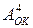 і
і 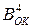 .
.
Обернений код суми чисел (А + В) за чотирирозрядним форматом визначимо за загальним правилом (1.110):
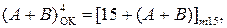 (1.111)
(1.111)
де (А + В) – сума аргументів функцій  і
і  .
.
У зв’язку з тим, що (15)m15 = 0, функцію (1.111) можна подати у такому вигляді:
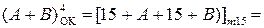
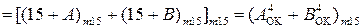 . (1.112)
. (1.112)
Таким чином, для обчислення 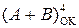 необхідно виконати дві мікрооперації:
необхідно виконати дві мікрооперації:

 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 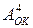 +
+ 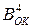 );
);




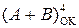 =[ EN NS S3S2S1] m15 ;
=[ EN NS S3S2S1] m15 ;
де EN NS S3S2S1 – повна п’ятирозрядна сума чотирирозрядних обернених кодів  і
і  ;
;

 EN NS - відповідно вихідне перенесення і стан знакового розряду суми (
EN NS - відповідно вихідне перенесення і стан знакового розряду суми (  +
+  );
);
S3S2S1 – рядок цифрових розрядів суми обернених кодів  і
і  .
.
Очевидно, що
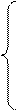





 NS S3S2S1, якщо EN = 0, цих міркувань випливає, що акового розряду суми (, тобто (
NS S3S2S1, якщо EN = 0, цих міркувань випливає, що акового розряду суми (, тобто (  +
+  )≤1510;
)≤1510;
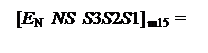


 EN NS S3S2S1 – 1510 = EN NS S3S2S1 – 1610+1 =
EN NS S3S2S1 – 1510 = EN NS S3S2S1 – 1610+1 =

 = EN NS S3S2S1 – 10000 + 0001 =
= EN NS S3S2S1 – 10000 + 0001 =
 = NS S3S2S1+0001, якщо EN = 1, тобто
= NS S3S2S1+0001, якщо EN = 1, тобто
(  +
+  ) ≥ 1610.
) ≥ 1610.
 З цих міркувань випливає, що
З цих міркувань випливає, що
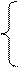
 NS S3S2S1, якщо EN = 0;
NS S3S2S1, якщо EN = 0;
 ( А+В)
( А+В) 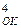 =
=
 NS S3S2S1 + 0001, якщо EN = 1.
NS S3S2S1 + 0001, якщо EN = 1.
Узагальнюючи, маємо:

 EN NS S3S2S1 = (
EN NS S3S2S1 = ( 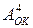 +
+ 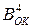 ); (1.113)
); (1.113)


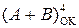 = NS S3S2S1+ 000 EN . (1.114)
= NS S3S2S1+ 000 EN . (1.114)



 Схемну реалізацію співвідношень (1.113) і (1.114) подано на рис.1.39. На суматорах першого рівня в схемі формується повна сума EN NS S3S2S1 обернених кодів
Схемну реалізацію співвідношень (1.113) і (1.114) подано на рис.1.39. На суматорах першого рівня в схемі формується повна сума EN NS S3S2S1 обернених кодів  і
і  . Для реалізації співвідношення (1.114) застосову-ється інкрементування проміжного коду NS S3S2S1 вихідним перенесенням EN суматора першого рівня.
. Для реалізації співвідношення (1.114) застосову-ється інкрементування проміжного коду NS S3S2S1 вихідним перенесенням EN суматора першого рівня.
Очевидно, що за допустимих значень аргументів А і В функцій 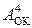 і
і  сума чисел (А+В) може перевищувати гранично-допустиме значення аргумента функції
сума чисел (А+В) може перевищувати гранично-допустиме значення аргумента функції 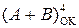 , яка обмежена проміжком числової осі між (-7) і (+7).
, яка обмежена проміжком числової осі між (-7) і (+7).
Передусім зазначимо, що за допустимих додатних значень оригіналів А і В їх сума (А + В) може визначатися проміжком числової осі між (+8) і (+14), тобто може перевищувати область визначення функції 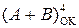 для пози-тивних значень аргументу (А + В). За цих умов згідно з алгоритмом (1.112) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки суматора.
для пози-тивних значень аргументу (А + В). За цих умов згідно з алгоритмом (1.112) потрібно формувати ознаку переповнення (ПП(А+В)) і сигнал позитивного переповнення (ППП(А+В)) розрядної сітки суматора.
Негативне переповнення суматора (ознака НПП(А+В)=1) виникає за допустимих від’ємних значень аргументів А і В функцій 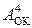 і
і  , які фор-мують множину чисел від (-14) до (-8). За цих умов згідно з алгоритмом (1.112) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і від’ємну ознаку негативного переповнення (НПП(А+В)) суматора обернених кодів.
, які фор-мують множину чисел від (-14) до (-8). За цих умов згідно з алгоритмом (1.112) потрібно сумісно формувати ознаку переповнення (ПП(А+В)) і від’ємну ознаку негативного переповнення (НПП(А+В)) суматора обернених кодів.
Для виявлення змінних суматора (1.112), які визначають переповнення розрядної сітки суматора обернених кодів за алгоритмом (1.112), розглянемо роботу суматора обернених кодів ( 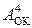 +
+  )m15, тобто суматора за модулем 15, за умови, коли сума чисел (А + В) утворює позитивне або негативне переповнення суматора оберненого коду (рис.1.39).
)m15, тобто суматора за модулем 15, за умови, коли сума чисел (А + В) утворює позитивне або негативне переповнення суматора оберненого коду (рис.1.39).
У разі позитивного переповнення (ознака ППП(А+В) = 1) при додаванні чисел у обернених кодах операнди 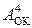 і
і  являють собою зображення виключно додатних чисел, тобто в цьому разі маємо: А = +МА, В = +МВ. Тому у цьому випадку згідно з (1.110)
являють собою зображення виключно додатних чисел, тобто в цьому разі маємо: А = +МА, В = +МВ. Тому у цьому випадку згідно з (1.110) 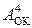 і
і  набувають вигляду:
набувають вигляду:
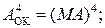
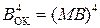 .
.
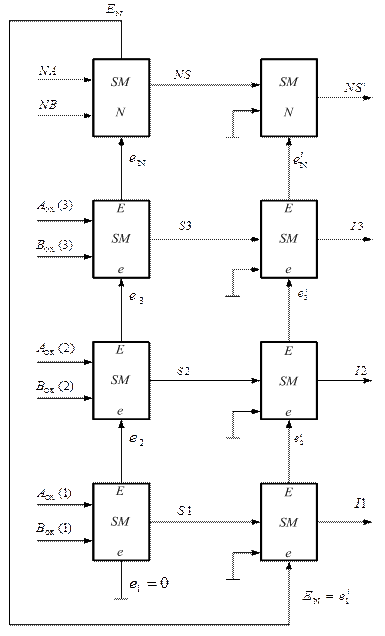
Рисунок 1.39 – Структурна схема суматора
для додавання чисел у обернених кодах:
 NS S3S2S1 = (
NS S3S2S1 = ( 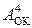 +
+  )m16;
)m16;

 NS i I3I2I1 = NS S3S2S1 + EN = (
NS i I3I2I1 = NS S3S2S1 + EN = ( 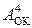 +
+  )m15;
)m15;
EN - вихідне перенесення повної суми обернених кодів 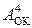 і
і  .
.
За цих умов повна п’ятирозрядна сума обернених кодів (рис.1.39) має значення:

 EN NS S3S2S1 =
EN NS S3S2S1 = 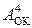 +
+  = (МА + МВ)5.
= (МА + МВ)5.

 За умови позитивного переповнення суматора, коли А+В = (+8)¸(+14) (рис.1.39), дістанемо:
За умови позитивного переповнення суматора, коли А+В = (+8)¸(+14) (рис.1.39), дістанемо:

 EN NS S3S2S1 = (МА + МВ)5 =
EN NS S3S2S1 = (МА + МВ)5 =

 = [(8) ¸ (14)] = 0 1 000 ¸ 0 1 110.
= [(8) ¸ (14)] = 0 1 000 ¸ 0 1 110.
Таким чином, за умови позитивного переповнення суматора ( 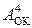 +
+  ) цифри на виводах суматора знакових розрядів NA i NB (рис.1.39) створюють наступну комбінацію булевих змінних:
) цифри на виводах суматора знакових розрядів NA i NB (рис.1.39) створюють наступну комбінацію булевих змінних:



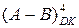

 = (16 – МА),
= (16 – МА),  = МА ):
= МА ):
 EN NS S(3/1) = (
EN NS S(3/1) = ( 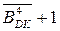 ) =
) =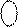

 =32 – [(-16) ¸ (-9)] = 16 ¸ 23 = 1 0 000 ¸ 1 0 111,
=32 – [(-16) ¸ (-9)] = 16 ¸ 23 = 1 0 000 ¸ 1 0 111,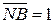 (NB = 0); NS = 0; EN = 1; eN = 0. ( 1.92 )
(NB = 0); NS = 0; EN = 1; eN = 0. ( 1.92 )

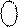
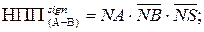
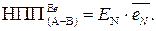 ( 1.94 )
( 1.94 )
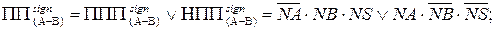 ( 1.95 )
( 1.95 )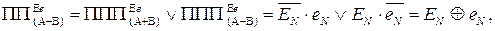 ( 1.96 )
( 1.96 )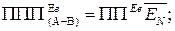 ( 1.97 )
( 1.97 )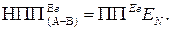 ( 1.98 )
( 1.98 )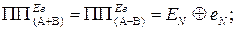 ( 1.99 )
( 1.99 )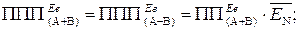 (1.100)
(1.100)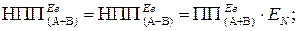 (1.101)
(1.101)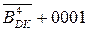 )5 =
)5 =

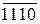 + 0001)5 = ( 1 101 + 0 001 + 0001)5 =
+ 0001)5 = ( 1 101 + 0 001 + 0001)5 =
 = (15)5 = 0 1 111 ( NS = 1, EN = 0, eN = 0 ).
= (15)5 = 0 1 111 ( NS = 1, EN = 0, eN = 0 ).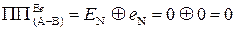 ;
; =
= 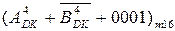 = ( 0 1 111)m16 = 1 111.
= ( 0 1 111)m16 = 1 111.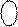
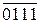 + 0001)5 = ( 1 010 + 1 000 + 0001)5 =
+ 0001)5 = ( 1 010 + 1 000 + 0001)5 =
 = 19 = 1 0 011 (EN = 1, NS = 0, eN = 0 );
= 19 = 1 0 011 (EN = 1, NS = 0, eN = 0 );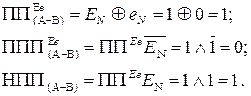
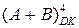 або
або 
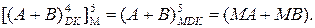


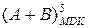 = NS2 NS1 S(3/1) = 0 0 000 ¸ 0 0 111. (1.102)
= NS2 NS1 S(3/1) = 0 0 000 ¸ 0 0 111. (1.102)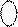
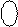
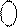
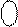


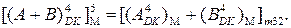 (1.104)
(1.104)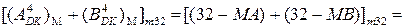
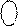

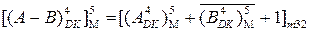 .
.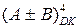 потрібно виконувати за еквівалентною формулою:
потрібно виконувати за еквівалентною формулою: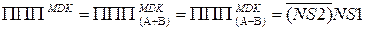 . (1.107)
. (1.107)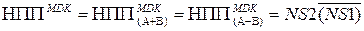 . (1.108)
. (1.108)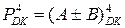 повинно мати активне значення за умови (рис.1.38) :
повинно мати активне значення за умови (рис.1.38) :
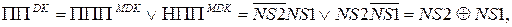 (1.109)
(1.109)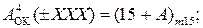
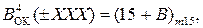 (1.110)
(1.110)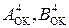 - відповідно обернені коди операндів А і В за чотири- розрядним форматом.
- відповідно обернені коди операндів А і В за чотири- розрядним форматом.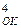 із використан-ням обернених кодів операндів
із використан-ням обернених кодів операндів 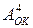 і
і 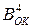 .
.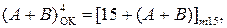 (1.111)
(1.111) і
і  .
.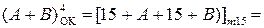
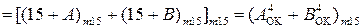 . (1.112)
. (1.112)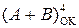 необхідно виконати дві мікрооперації:
необхідно виконати дві мікрооперації:


 EN NS - відповідно вихідне перенесення і стан знакового розряду суми (
EN NS - відповідно вихідне перенесення і стан знакового розряду суми ( 


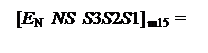
 = NS S3S2S1+0001, якщо EN = 1, тобто
= NS S3S2S1+0001, якщо EN = 1, тобто
 ( А+В)
( А+В)  EN NS S3S2S1 = (
EN NS S3S2S1 = ( 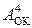 і
і 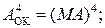
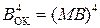 .
.
 NS S3S2S1 = (
NS S3S2S1 = ( 
 NS i I3I2I1 = NS S3S2S1 + EN = (
NS i I3I2I1 = NS S3S2S1 + EN = ( 
 EN NS S3S2S1 = (МА + МВ)5 =
EN NS S3S2S1 = (МА + МВ)5 =
 = [(8) ¸ (14)] = 0 1 000 ¸ 0 1 110.
= [(8) ¸ (14)] = 0 1 000 ¸ 0 1 110.