ААК / 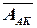
В спрощеному блоці за алгоритмом 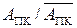 мікрооперації (1.63), (1.69) та (1.72) реалізовані з використанням одного суматора з відповідним допоміжним обрамленням. Можлива структура спрощеного пристрою наведена на рис.1.30.
мікрооперації (1.63), (1.69) та (1.72) реалізовані з використанням одного суматора з відповідним допоміжним обрамленням. Можлива структура спрощеного пристрою наведена на рис.1.30.
У кожному циклі роботи суматор пристрою виконує одну із трьох можливих мікрооперацій, що досягається активізацією відповідних керуючих сигналів, які формуються згідно з мікропрограмою роботи пристрою (рис.1.31). Обчислення результату починається за стартовим сигналом «ADD» або «SUB». Далі суматор має полічити прямий код суми або різниці прямих кодів операндів. Результуюча мікрооперація визначається ознакою DМ, тобто кодом операції над модулями чисел. За кодом DМ = 0 виконується звичайне підсумовування кодів (АПК+МВ) із визначенням ознаки переповнення розрядної сітки модуля результату ППМР. Субоперація віднімання модулів чисел за кодом DМ = 1 виконується значно складніше. У загальному випадку операція виконується покроково. На першому етапі припускається, що МА≥MB і в пристрої виконується мікрооперація 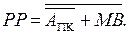 Якщо при цьому утворюється ознака
Якщо при цьому утворюється ознака 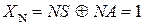 (що еквівалентно ω=1), операція у пристрої закінчується. У протилежному випадку, коли на першому етапі отримуємо XN = 0, виконується наступний крок, в якому обчислюється симетрична різниця модулів чисел. Для цього операційний суматор конфігурується на виконання мікрооперацій:
(що еквівалентно ω=1), операція у пристрої закінчується. У протилежному випадку, коли на першому етапі отримуємо XN = 0, виконується наступний крок, в якому обчислюється симетрична різниця модулів чисел. Для цього операційний суматор конфігурується на виконання мікрооперацій:
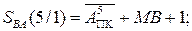
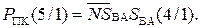
Після отримання правильного результату пристрій керування повертається у початковий стан і очікує наступної інструкції.

Рисунок 1.29,б - Модуль 2 арифметичного пристрою для додавання
і віднімання чисел у прямих кодах за алгоритмом АПК/ 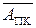
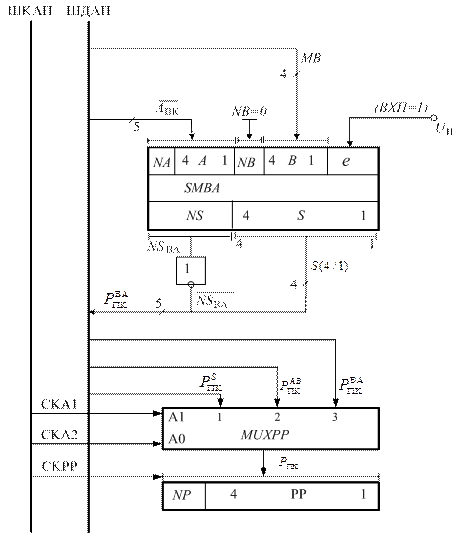
Рисунок 1.29,в - Модуль 3 арифметичного пристрою для додавання
і віднімання чисел у прямих кодах за алгоритмом АПК/ 
1.3 Теоретичні засади та структура арифметичних пристроїв для додавання і віднімання чисел у доповняльних кодах
Для ілюстрації основних особливостей побудови арифметичних пристроїв для додавання чисел у доповняльних кодах розглянемо обчислювачі за чотирирозрядним форматом.
Як вказувалося, доповняльні коди за чотирирозрядним форматом обчислюються за виразами:
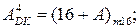
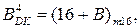 ( 1.74 )
( 1.74 )
де А = ±МА, В = ± МВ, МА, МВ – відповідно модулі операндів А і В;
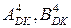 - чотирирозрядні машинні зображення доповняльних кодів відповідно чисел А і В, обмежених у проміжку числової осі між (-8) і (+7);
- чотирирозрядні машинні зображення доповняльних кодів відповідно чисел А і В, обмежених у проміжку числової осі між (-8) і (+7);
16 – кількість станів доповняльного коду за чотирирозрядним форматом (зміщення чотирирозрядного доповняльного коду).
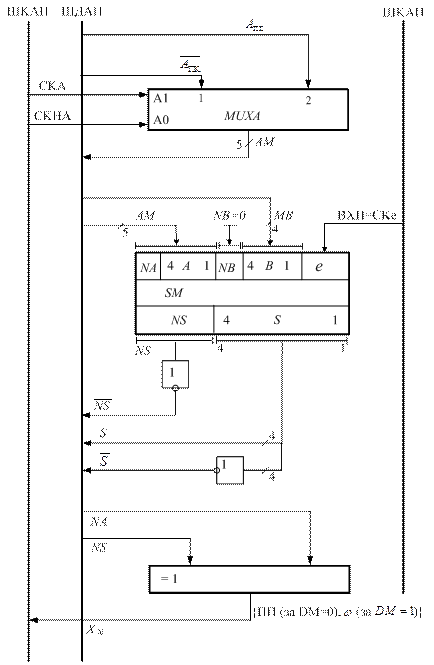
Рисунок 1.30,а – Модуль 1 спрощеного арифметичного пристрою для додавання і віднімання чисел у прямих кодах за алгоритмом АПК/ 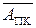
Побудуємо схему для обчислення суми чисел 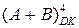 за допомогою доповняльних кодів
за допомогою доповняльних кодів  і
і  .
.
Доповняльний код суми чисел (А+В) визначимо за загальним правилом (1.74) співвідношенням:
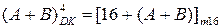 , ( 1.75 )
, ( 1.75 )
де 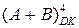 - чотирипозиційний доповняльний код суми чисел (А + В), визначеної в межах числової осі між (-8) і (+7).
- чотирипозиційний доповняльний код суми чисел (А + В), визначеної в межах числової осі між (-8) і (+7).
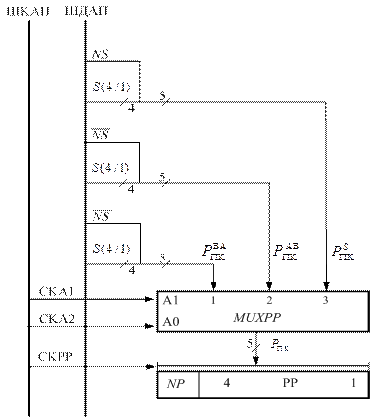
Рисунок 1.30,б – Модуль 2 спрощеного арифметичного пристрою для додавання і віднімання чисел у прямих кодах за алгоритмом АПК/ 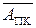
У зв’язку з тим, що (16)m16 = 0, функцію (1.75) можна представити у вигляді:
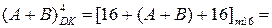

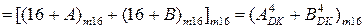 ( 1.76 )
( 1.76 )
Очевидно, що аргументи А і В функцій  та
та  згідно з (1.74) у деяких випадках формують суму (А + В), яка перевищує гранично-допустиме значення аргументу (А + В) функції
згідно з (1.74) у деяких випадках формують суму (А + В), яка перевищує гранично-допустиме значення аргументу (А + В) функції 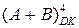 (рис.1.32). Визначимо способи фіксації випадків переповнення функції (1.76).
(рис.1.32). Визначимо способи фіксації випадків переповнення функції (1.76).
Передусім зазначимо, що за допустимих додатних значень аргументів А і В функцій  та
та  (які обмежені проміжком між (0) і (+7)) сума (А+В) переповнює розрядну сітку за умови, коли утворює множину чисел від (+8) до (+14), яка перевищує область визначення функції
(які обмежені проміжком між (0) і (+7)) сума (А+В) переповнює розрядну сітку за умови, коли утворює множину чисел від (+8) до (+14), яка перевищує область визначення функції 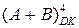 за позитивних значень аргументів. За цих умов суматором доповняльних кодів за алгорит-мом (1.76) (рис.1.33), повинна формуватися ознака переповнення ПП(А+В) і сигнал позитивного переповнення (ППП(А+В)).
за позитивних значень аргументів. За цих умов суматором доповняльних кодів за алгорит-мом (1.76) (рис.1.33), повинна формуватися ознака переповнення ПП(А+В) і сигнал позитивного переповнення (ППП(А+В)).
Негативне переповнення (НПП(А+В)) функції 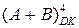 виникає за допустимих від’ємних значень аргументів [А = (-8) ¸ (-1), В=(-8)¸(-1)], які сумісно формують множину чисел між (-9) і (-16). За цих умов суматором доповняльних кодів ( SMDK ) повинна формуватися ознака переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)).
виникає за допустимих від’ємних значень аргументів [А = (-8) ¸ (-1), В=(-8)¸(-1)], які сумісно формують множину чисел між (-9) і (-16). За цих умов суматором доповняльних кодів ( SMDK ) повинна формуватися ознака переповнення (ПП(А+В)) і сигнал негативного переповнення (НПП(А+В)).
Для виявлення змінних SMDK (рис.1.33), які визначають переповнення його розрядної сітки, розглянемо стан SMDK за умови, коли сума аргументів (А+В) перевищує область визначення доповняльного коду суми чисел (А+В).
У разі позитивного переповнення (за ознакою ППП(А+В) =1) при додаванні доповняльних кодів операнди суматора  і
і  являють зображення виключно додатних чисел, тобто у цьому разі ( за ППП(А+В) = 1) маємо А = (+МА), В = (+МВ).
являють зображення виключно додатних чисел, тобто у цьому разі ( за ППП(А+В) = 1) маємо А = (+МА), В = (+МВ).
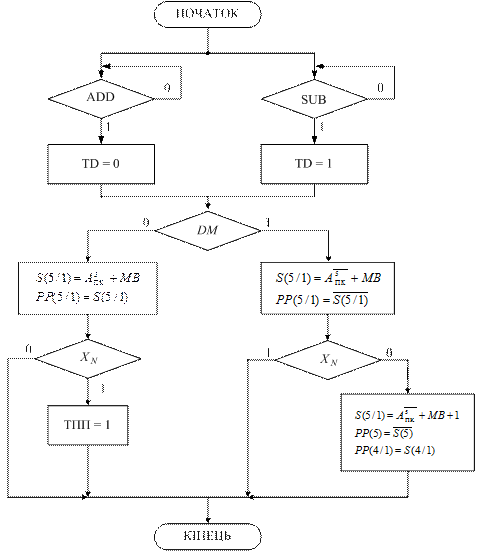
Рисунок 1.31 – Граф мікропрограми спрощеного арифметичного
пристрою для додавання і віднімання чисел у прямих кодах
за алгоритмом АПК/ 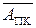
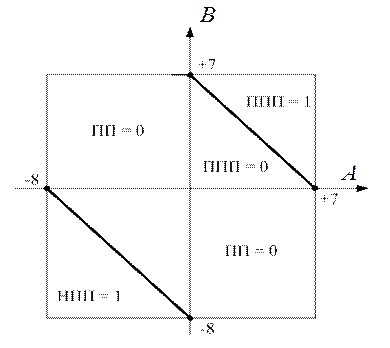
Рисунок 1.32 – Зони переповнення функції 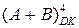 залежно від
залежно від
знаків аргументів А і В:
НПП, ППП – відповідно ознака негативного і позитивного переповнення функції 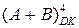 - доповняльного коду суми чисел (А+В) за чотирирозрядним форматом.
- доповняльного коду суми чисел (А+В) за чотирирозрядним форматом.
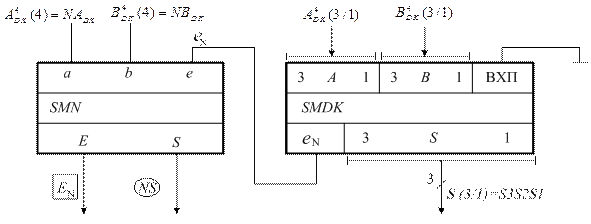
Рисунок 1.33 – Структурна схема суматора доповняльних кодів (SMDK ):
NA, NB – знакові розряди доповняльних кодів;
EN, eN – відповідно вихідне і вхідне перенесення суматора знакових розрядів;

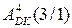 ,
, 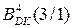 - цифрова частина відповідно доповняльного коду
- цифрова частина відповідно доповняльного коду  і
і  ;
;
 EN NS S(3/1) – повний числовий вираз стану суматора чотирирозрядних доповняльних кодів.
EN NS S(3/1) – повний числовий вираз стану суматора чотирирозрядних доповняльних кодів.
Отже, за згаданих умов коди  і
і  набувають вигляду:
набувають вигляду:
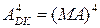 ;
; 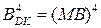 .
.
Тому повна п’ятирозрядна сума доповняльних кодів  і
і  на виходах SMDK (рис.1.33) набуває значення:
на виходах SMDK (рис.1.33) набуває значення:

 EN NS S3S2S1 =
EN NS S3S2S1 = 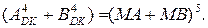
За умови позитивного переповнення, коли (МA + МВ) = [(+8) ¸ (+14)], дістанемо:

 EN NS S3S2S1 =
EN NS S3S2S1 = 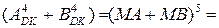

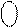

 = 0 1 000 ¸ 0 1 110.
= 0 1 000 ¸ 0 1 110.
Таким чином, за умови позитивного переповнення функції 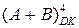 у знакових розрядах NA і NB суматора (рис.1.33) утворюється наступна комбінація булевих змінних:
у знакових розрядах NA і NB суматора (рис.1.33) утворюється наступна комбінація булевих змінних:
NA = 0; NB = 0; NS = 1; EN = 0; eN = 1. ( 1.77 )
У випадку, коли ознака ППП(А+В) = 0, при додаванні додатних чисел А і В сума модулів (МА+МВ) змінюється в межах від 0 до 7 і на виводах суматора (  +
+  ) створюється рядок двійкових цифр:
) створюється рядок двійкових цифр:
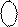

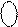


 (
(  +
+  ) = EN NS S3S2S1 = (MA + MB)5 = 0 0 000 ¸ 0 0 111.
) = EN NS S3S2S1 = (MA + MB)5 = 0 0 000 ¸ 0 0 111.
Отже, змінні суматора NA, NB і NS (рис.1.33) за коректного значення доповняльного коду суми (А + В) мають значення:
NA = 0; NB = 0; NS = 0; EN = 0; eN = 0. ( 1.78 )
Таким чином, за алгоритмом (1.76) позитивне переповнення суматора (  +
+  ) потрібно обчислювати за булевими виразами (табл.1.3):
) потрібно обчислювати за булевими виразами (табл.1.3):
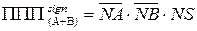 ; ( 1.79 )
; ( 1.79 )
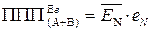 . ( 1.80 )
. ( 1.80 )
Таблиця 1.3 - Визначення ознаки ППП функції 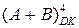

За алгоритмом (1.76) при додаванні від’ємних чисел А і В можливе не-гативне переповнення (ознака НПП(А+В)=1) функції 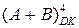 за допустимих значень аргументів доданків
за допустимих значень аргументів доданків  і
і  суматора доповняльних кодів (рис.1.33). У цьому випадку операнди А і В мають виключно від’ємні
суматора доповняльних кодів (рис.1.33). У цьому випадку операнди А і В мають виключно від’ємні
значення, тобто А = -МА і В = -МВ, причому за ознакою НПП(А+В) = 1, очевидно, (МА + МВ) являють собою множину чисел від 9 до 16. Звідси отримаємо (рис.1.33):

 EN NS S(3/1) = (
EN NS S(3/1) = (  +
+  ) = (16 – МА) + (16 – МВ) =
) = (16 – МА) + (16 – МВ) =

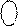

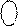 = 32 – (МА + МВ) =32 – (9 ¸ 16) = 23 ¸ 16 = 1 0 111 ¸ 1 0 000.
= 32 – (МА + МВ) =32 – (9 ¸ 16) = 23 ¸ 16 = 1 0 111 ¸ 1 0 000.
Таким чином, за умови, коли ознака НПП(А=В) = 1, змінні суматора NA і NB доповняльних кодів  і
і  складають двійковий набір (рис.1.33): NA = 1; NB = 1; NS = 0; EN = 1; eN = 0.
складають двійковий набір (рис.1.33): NA = 1; NB = 1; NS = 0; EN = 1; eN = 0.
У випадку, коли при додаванні від’ємних чисел А і В ознака НПП(А+В)=0, тобто, якщо (МА+МВ)=1¸ 8, повна сума суматора доповняльних кодів (рис.1.33) оцінюється співвідношенням:
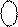

 EN NS S(3/1) = (
EN NS S(3/1) = (  +
+  ) = (16 – МА) + (16 – МВ) =
) = (16 – МА) + (16 – МВ) =

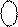
 =32 – (МА + МВ) =32 – (8 ¸ 1) = 24 ¸ 31 = 1 1 000 ¸ 1 1 111.
=32 – (МА + МВ) =32 – (8 ¸ 1) = 24 ¸ 31 = 1 1 000 ¸ 1 1 111.
Отже, за відсутності переповнення суматора змінні SMN (рис.1.33) набувають значень: NA = 1; NB = 1; NS = 1; EN = 1; eN = 1.
Таким чином ознака НПП(А+В) функції (1.76) визначається наступними виразами (табл.1.4):
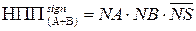 ; ( 1.81 )
; ( 1.81 )
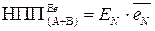 . ( 1.82 )
. ( 1.82 )
Таблиця 1.4 - Визначення ознаки НПП функції 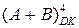
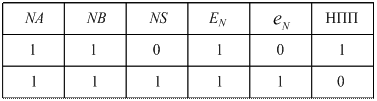
Отже, при додаванні чисел одного знаку (перший і третій квадрант змінних А і В на рис. 1.32) ознаку переповнення (ПП(А+В)) функції 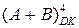 згідно з (1.79) ¸ (1.82) потрібно фіксувати за допомогою одного із булевих виразів:
згідно з (1.79) ¸ (1.82) потрібно фіксувати за допомогою одного із булевих виразів:
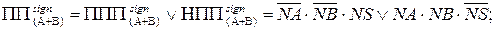 ( 1.83 )
( 1.83 )
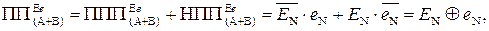 ( 1.84 )
( 1.84 )
причому
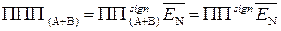 ; ( 1.85 )
; ( 1.85 )
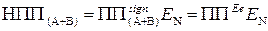 . ( 1.86 )
. ( 1.86 )
Структурна схема пристрою для додавання чисел у доповняльних кодах подана на рис.1.34. Схема містить :
- РА, РВ – регістри для зберігання доповняльних кодів чисел А і В;
- РР – регістр результату для завантаження і зберігання суми чисел у доповняльному коді;
- ТПП – тригер переповнення розрядної сітки РР;
- НПП і ППП – схеми для вироблення негативного і позитивного переповнення розрядної сітки пристрою;
- SMDK – суматор доповняльних кодів операндів;
- СS,СПП, СРР – сигнали керування місцевого пристрою управління арифметичного модуля;
- КА, КВ, КР – керуючі сигнали центрального пристрою керування комп’ютера.
Для ілюстрації роботи арифметичного пристрою розглянемо типові приклади додавання чисел у доповняльних кодах.
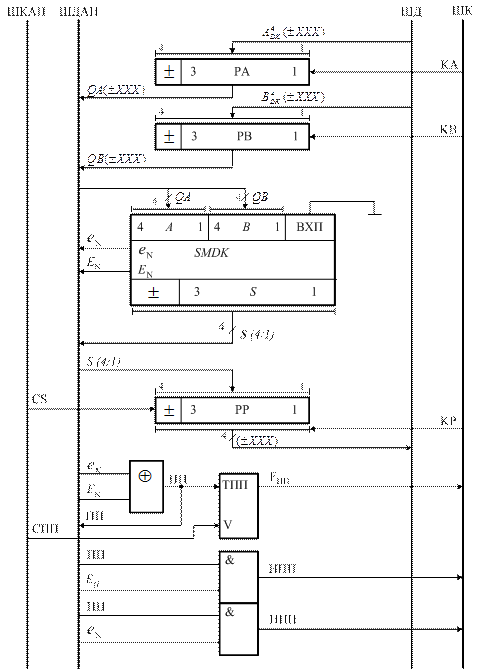
Рисунок 1.34 – Структурна схема арифметичного
пристрою для додавання чисел у доповняльних кодах
Припустімо, що потрібно обчислити суму (А + В) у доповняльному коді за таких значень аргументів: А = - 011; В = - 010.
За цих умов у арифметичному пристрої доповняльних кодів (рис.1.33, 1.34) отримаємо:





 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5 =( 1 101 + 1 110 )5 = 1 1 011 (eN = 1);
)5 =( 1 101 + 1 110 )5 = 1 1 011 (eN = 1);




 PP =
PP = 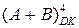 = ( EN NS S3S2S1)m16= [ 1 1 011]m16 = 1 011 =
= ( EN NS S3S2S1)m16= [ 1 1 011]m16 = 1 011 = 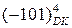 ;
;
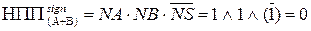 ;
;

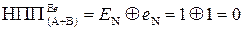 .
.
Розглянемо далі приклад, що ілюструє негативне переповнення розрядної сітки при додаванні від’ємних чисел.
Припустімо, що потрібно знайти суму (А + В) за таких значень аргументів: А = - 110, В = - 111.
За цих умов двійкові коди та ознаки операції додавання чисел у арифметичному пристрої доповняльних кодів (рис.1.33,1.34) набувають таких значень:

 EN NS S3S2S1 = (
EN NS S3S2S1 = (  +
+  )5m16 =
)5m16 =

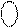

 = ( 1 010 + 1 001)5m16= 1 0 011 (еN = 0);
= ( 1 010 + 1 001)5m16= 1 0 011 (еN = 0);
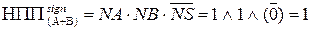 ;
;


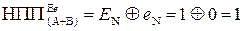 .
.
 Таким чином, у цьому разі (
Таким чином, у цьому разі (  +
+  )m16 = 0 011 ¹
)m16 = 0 011 ¹ 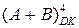 , тобто довжина суми (А + В) перевищує розрядну сітку регістра результату (РР).
, тобто довжина суми (А + В) перевищує розрядну сітку регістра результату (РР).
Побудуємо тепер схему для обчислення різниці чисел 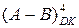 за допомогою доповняльних кодів
за допомогою доповняльних кодів  і
і  .
.
При застосуванні чотирирозрядних доповняльних кодів згідно з загальним правилом обчислення доповняльного коду різниця чисел (А-В) у доповняльному коді повинна обчислюватися за формулою:
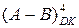 = [16 + (A - B)]m16.
= [16 + (A - B)]m16.
Для спрощення обчислювача коду 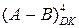 формулу далі перетворимо наступним чином:
формулу далі перетворимо наступним чином:
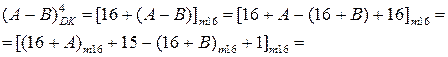
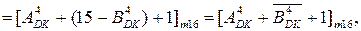 ( 1.87 )
( 1.87 )
де 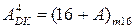 ,
, 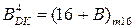 - відповідно зображення чисел А і В у доповняльних кодах;
- відповідно зображення чисел А і В у доповняльних кодах;
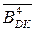 - інвертоване значення
- інвертоване значення  .
.
Як відомо, функції  і
і  визначені у проміжку числової осі між (-8) і (+7). Тому формула (1.87) дійсна тільки для тих зображень А і В, які
визначені у проміжку числової осі між (-8) і (+7). Тому формула (1.87) дійсна тільки для тих зображень А і В, які
сумісно не перевищують область визначення функції 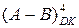 , тобто їх різниця змінюється в межах від (-8) до (+7). Таким чином, позитивне переповнення функції
, тобто їх різниця змінюється в межах від (-8) до (+7). Таким чином, позитивне переповнення функції 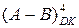 виникає за умови, коли А = +МА, В = -МВ і (А – В) = =+(МА + МВ) = (+8) ¸ (+14). Негативне переповнення функції (1.87) виникає за умови, коли А =-МА, В = + МВ і (А–В) = -(МА + МВ) = (-9) ¸ (-16). На рис.1.35 ці зони переповнення визначені трикутниками в четвертому і другому квадрантах змінних А і В.
виникає за умови, коли А = +МА, В = -МВ і (А – В) = =+(МА + МВ) = (+8) ¸ (+14). Негативне переповнення функції (1.87) виникає за умови, коли А =-МА, В = + МВ і (А–В) = -(МА + МВ) = (-9) ¸ (-16). На рис.1.35 ці зони переповнення визначені трикутниками в четвертому і другому квадрантах змінних А і В.
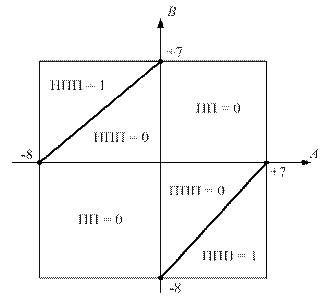
Рисунок 1.35 – Зони переповнення розрядної сітки чотирирозрядного
доповняльного коду різниці чисел (А-В) залежно від знаків аргументів А і В:
ППП, НПП – відповідно зони позитивного і негативного переповнення
функції 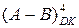
За умови позитивного переповнення (ознака ППП(А-В) =1), коли (А -В) = =(+8) ¸ (+14), повна сума на виходах суматора складає код:
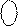
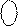

 EN NS S3S2S1 =
EN NS S3S2S1 =  +
+ 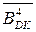 + 1 = МА + 15 -
+ 1 = МА + 15 -  + 1 =
+ 1 =

 = MA + 16 - (16 – МВ) = МА + МВ) = (8 ¸ 14) = ( 0 1 000 ¸ 0 1 110.
= MA + 16 - (16 – МВ) = МА + МВ) = (8 ¸ 14) = ( 0 1 000 ¸ 0 1 110.
Таким чином, за ознакою ППП(А-В) = 1 змінні SMN (рис.1.36) прий-мають значення:
NA = 0; 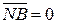 (NB = 1); NS = 1; EN = 0; eN = 1. ( 1.88 )
(NB = 1); NS = 1; EN = 0; eN = 1. ( 1.88 )
Якщо при А > 0 і В < 0 ознака ППП(А-В) = 0, то (А – В) = (0) ¸ (+7) і повна сума на виводах суматора утворює код:

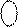
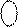


 EN NS S3S2S1) = (
EN NS S3S2S1) = (  +
+ 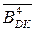 + 1) =(МА + МВ)5 = 0 0 000 ¸ 0 0 111.
+ 1) =(МА + МВ)5 = 0 0 000 ¸ 0 0 111.
Отже, за умови, коли ознака ППП(А-В) = 0, змінні суматора знакових розрядів  і
і  набувають значень (рис.1.36):
набувають значень (рис.1.36):
NA = 0; 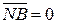 (NB = 1); NS = 0; EN = 0; eN = 0.
(NB = 1); NS = 0; EN = 0; eN = 0.
Виходячи з цих міркувань, побудована таблиця істинності функції ППП(А-В) (табл. 1.5). Звідкіль дістанемо:
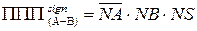 ; ( 1.90 )
; ( 1.90 )
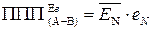 . ( 1.91 )
. ( 1.91 )
Ознака негативного переповнення функції (1.85) виникає виключно у другому квадранті змінних А і В (рис.1.35) за умови, коли:
(А – В) = - (МА + МВ) = (-16) ¸ (-9).


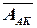
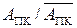 мікрооперації (1.63), (1.69) та (1.72) реалізовані з використанням одного суматора з відповідним допоміжним обрамленням. Можлива структура спрощеного пристрою наведена на рис.1.30.
мікрооперації (1.63), (1.69) та (1.72) реалізовані з використанням одного суматора з відповідним допоміжним обрамленням. Можлива структура спрощеного пристрою наведена на рис.1.30.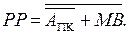 Якщо при цьому утворюється ознака
Якщо при цьому утворюється ознака 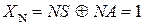 (що еквівалентно ω=1), операція у пристрої закінчується. У протилежному випадку, коли на першому етапі отримуємо XN = 0, виконується наступний крок, в якому обчислюється симетрична різниця модулів чисел. Для цього операційний суматор конфігурується на виконання мікрооперацій:
(що еквівалентно ω=1), операція у пристрої закінчується. У протилежному випадку, коли на першому етапі отримуємо XN = 0, виконується наступний крок, в якому обчислюється симетрична різниця модулів чисел. Для цього операційний суматор конфігурується на виконання мікрооперацій: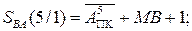
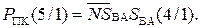

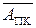

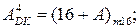
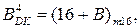 ( 1.74 )
( 1.74 )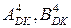 - чотирирозрядні машинні зображення доповняльних кодів відповідно чисел А і В, обмежених у проміжку числової осі між (-8) і (+7);
- чотирирозрядні машинні зображення доповняльних кодів відповідно чисел А і В, обмежених у проміжку числової осі між (-8) і (+7);
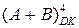 за допомогою доповняльних кодів
за допомогою доповняльних кодів  і
і  .
.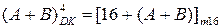 , ( 1.75 )
, ( 1.75 )
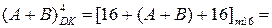

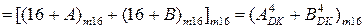 ( 1.76 )
( 1.76 )



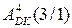 ,
, 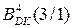 - цифрова частина відповідно доповняльного коду
- цифрова частина відповідно доповняльного коду  EN NS S(3/1) – повний числовий вираз стану суматора чотирирозрядних доповняльних кодів.
EN NS S(3/1) – повний числовий вираз стану суматора чотирирозрядних доповняльних кодів.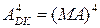 ;
; 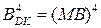 .
.
 EN NS S3S2S1 =
EN NS S3S2S1 = 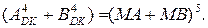

 EN NS S3S2S1 =
EN NS S3S2S1 = 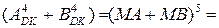





 (
( 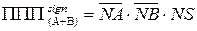 ; ( 1.79 )
; ( 1.79 )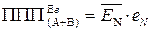 . ( 1.80 )
. ( 1.80 )

 EN NS S(3/1) = (
EN NS S(3/1) = ( 
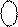

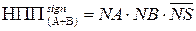 ; ( 1.81 )
; ( 1.81 )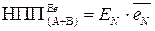 . ( 1.82 )
. ( 1.82 )
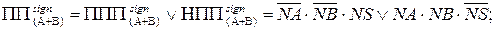 ( 1.83 )
( 1.83 )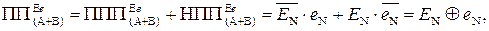 ( 1.84 )
( 1.84 )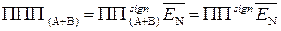 ; ( 1.85 )
; ( 1.85 )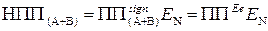 . ( 1.86 )
. ( 1.86 )

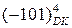 ;
;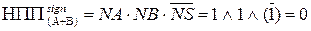 ;
;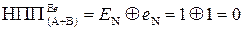 .
. EN NS S3S2S1 = (
EN NS S3S2S1 = ( 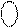
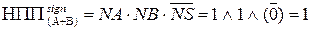 ;
;
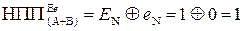 .
. Таким чином, у цьому разі (
Таким чином, у цьому разі ( 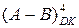 за допомогою доповняльних кодів
за допомогою доповняльних кодів 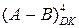 формулу далі перетворимо наступним чином:
формулу далі перетворимо наступним чином: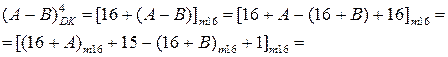
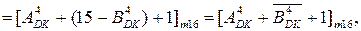 ( 1.87 )
( 1.87 )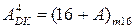 ,
, 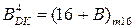 - відповідно зображення чисел А і В у доповняльних кодах;
- відповідно зображення чисел А і В у доповняльних кодах;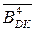 - інвертоване значення
- інвертоване значення 
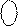
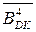 + 1 = МА + 15 -
+ 1 = МА + 15 - 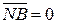 (NB = 1); NS = 1; EN = 0; eN = 1. ( 1.88 )
(NB = 1); NS = 1; EN = 0; eN = 1. ( 1.88 )
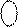

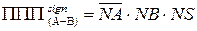 ; ( 1.90 )
; ( 1.90 )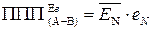 . ( 1.91 )
. ( 1.91 )