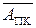ААК / 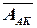
Згідно із загальним алгоритмом за кодом операції над модулями DМ =0 п’ятирозрядний прямий код результату слід визначати за формулою:
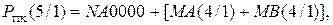 ( 1.62 )
( 1.62 )
де 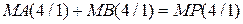 - чотирирозрядний модуль результату у нормальній формі;
- чотирирозрядний модуль результату у нормальній формі;
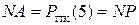 - правильний знак результату за DМ = 0.
- правильний знак результату за DМ = 0.
У зв’язку з тим, що згідно з визначенням прямого коду
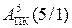 = NA 0000 + MA(4/1),
= NA 0000 + MA(4/1),
 вираз (1.62) можна подати у вигляді:
вираз (1.62) можна подати у вигляді:
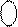
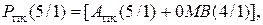 ( 1.63 )
( 1.63 )
де 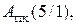
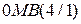 - відповідно п’ятирозрядний прямий код операнда А і п’ятипозиційний код модуля операнда В.
- відповідно п’ятирозрядний прямий код операнда А і п’ятипозиційний код модуля операнда В.
При цьому, згідно з (1.62) і (1.63) знаковий розряд результату буде формуватися за формулою:
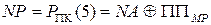 ( 1.64 )
( 1.64 )
де ППМР – ознака переповнення розрядної сітки модуля результату МР(4/1) при додаванні модулів МА(4/1) + МВ(4/1).
Таким чином, загалом при визначенні результату за співвідношенням (1.63) отримаємо:
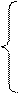 NA, якщо МА(4/1)+МВ(4/1) ≤ 15;
NA, якщо МА(4/1)+МВ(4/1) ≤ 15;
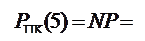
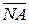 , якщо МА(4/1)+МВ(4/1) ≥ 16, тобто
, якщо МА(4/1)+МВ(4/1) ≥ 16, тобто
при переповненні розрядної сітки (довжини) модуля результату МР(4/1).
Отже, ознаку переповнення розрядної повної сітки модуля результату МР(4/1) у суматорі (1.63) остаточно можна подати у вигляді:
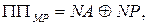 ( 1.65 )
( 1.65 )
де 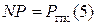 - значення п’ятого розряду повної суми
- значення п’ятого розряду повної суми 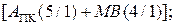
NA – позначення знакового розряду операнда А.
Покажемо застосування алгоритму (1.63) на деяких типових прикладах.
Припустімо, що треба виконати додавання чисел у прямих кодах (А  +В
+В  ) у випадку, коли
) у випадку, коли
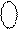 А
А  = 1 0110 (NA=1, MA=0110),
= 1 0110 (NA=1, MA=0110),
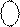 B
B  = 1 0111 (NB =1, MD = 0111).
= 1 0111 (NB =1, MD = 0111).
Очевидно, що за цих умов
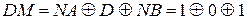 = 0.
= 0.
Тоді згідно з (1.63) маємо:
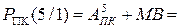 1 0110 + 0 0111 = 1 1101,
1 0110 + 0 0111 = 1 1101,
де NP = PПК(5) = 1; МР(4/1) = 1101.
 Звідси згідно з (1.65) отримаємо:
Звідси згідно з (1.65) отримаємо:
ППМР = 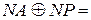 1
1  1 = 0.
1 = 0.
Припустімо тепер, що треба виконати віднімання прямих кодів (А5ПК -В5ПК) у випадку, коли
 А
А  = 1 1101 (NA=1, MA=1101),
= 1 1101 (NA=1, MA=1101),
 B
B  = 0 0111 (NВ=0, MВ=0111).
= 0 0111 (NВ=0, MВ=0111).


 Очевидно, що за цих умов
Очевидно, що за цих умов
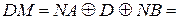 1
1  1
1  0 = 0.
0 = 0.
Тоді результат можна визначити за формулою (1.63):
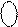
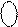
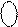
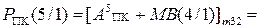 [ 1 1101+ 0 0111]m16 = 0 0100,
[ 1 1101+ 0 0111]m16 = 0 0100,
де NP = PПК(5) = 0.
 Звідси згідно з (1.65) отримаємо
Звідси згідно з (1.65) отримаємо
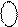 ППМР =
ППМР = 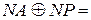 1
1  0 = 1.
0 = 1.
Це означає, що результат PПК(5/1) за цих значень аргументів є помилковим.
Згідно із загальними правилами арифметики за кодом операції над модулями DМ = 1 і за умови МА(4/1) ≥ МВ(4/1) (тобто за ознакою ω = 1) результат у прямому коді визначається рівнянням:
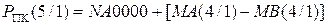 ( 1.66 )
( 1.66 )
де 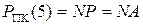 - знак результату за умови ω = 1;
- знак результату за умови ω = 1;
МР(4/1) = МА(4/1) – МВ(4/1) – модуль результату;
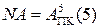 - знак прямого коду числа А.
- знак прямого коду числа А.
У зв’язку з тим, що згідно з визначенням прямого коду
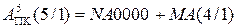
вираз (1.66) можна подати у вигляді:
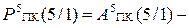 0 МВ(4/1). ( 1.67 )
0 МВ(4/1). ( 1.67 )
Для спрощення схемної реалізації виразу (1.67) утворимо функцію:
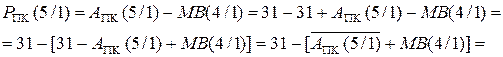
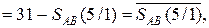 ( 1.68 )
( 1.68 )
де 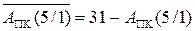 ;
;

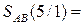 NSAB SAB(4/1) =
NSAB SAB(4/1) = 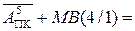
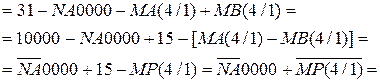
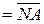
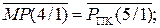
 NA MP(4/1) – прямий код результату за умови, коли МА(4/1) ≥ МВ(4/1);
NA MP(4/1) – прямий код результату за умови, коли МА(4/1) ≥ МВ(4/1);
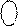
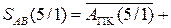 0 МВ(4/1);
0 МВ(4/1);
РПК(5/1) = 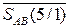 - порозрядна інверсія коду
- порозрядна інверсія коду 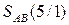 ;
;
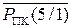 - порозрядна інверсія п’ятирозрядного коду
- порозрядна інверсія п’ятирозрядного коду 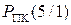 .
.
У зв’язку з тим, що:
SAB(4/1) = 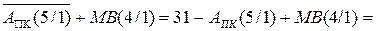
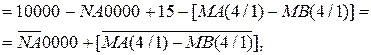
маємо
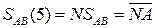 ,
,
Таким чином, при виконанні (за DМ = 1) мікрооперації
 SAB(5/1) =
SAB(5/1) = 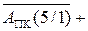 0 МВ(4/1), ( 1.69 )
0 МВ(4/1), ( 1.69 )
згідно з (1.68) ознака відношення модулів визначається за формулою
ω = 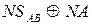 , ( 1.70 )
, ( 1.70 )
де 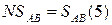 - позначення знакового розряду повної суми операції (1.69).
- позначення знакового розряду повної суми операції (1.69).
Звісно, що за кодом операції над модулями DМ=1 і за умови МВ(4/1)>МА(4/1), результат операції 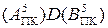 у прямому коді визначається формулою:
у прямому коді визначається формулою:
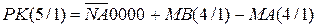 ( 1.71 )
( 1.71 )
де 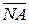 - правильний знак результату;
- правильний знак результату;
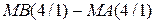 - правильний модуль результату;
- правильний модуль результату;
Для спрощення схемної реалізації перетворимо (1.71) наступним чином:
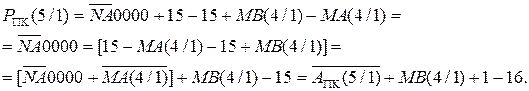
Якщо 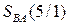 визначити за формулою
визначити за формулою

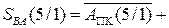 0 МВ(4/1) + 1, ( 1.72 )
0 МВ(4/1) + 1, ( 1.72 )
то
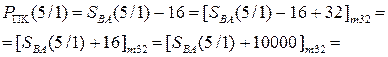
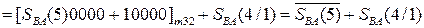 , ( 1.73 )
, ( 1.73 )
де 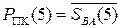 - знак прямого коду результату;
- знак прямого коду результату;
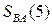 - значення п’ятого розряду суматора (1.72);
- значення п’ятого розряду суматора (1.72);
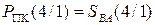 - модуль результату ;
- модуль результату ;
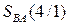 - чотирирозрядний рядок молодших цифр суматора (1.72);
- чотирирозрядний рядок молодших цифр суматора (1.72);
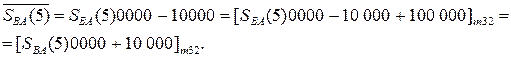
Покажемо застосування цих алгоритмів за деяких значень прямих кодів.
Припустімо, що треба виконати операцію (А  + В
+ В  ) у випадку, коли
) у випадку, коли
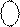
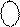 А
А  (5/1) = 1 1101 (NA=1, MA=1101),
(5/1) = 1 1101 (NA=1, MA=1101),
B  (5/1) = 0 0111 (NВ=0, MВ=0111).
(5/1) = 0 0111 (NВ=0, MВ=0111).
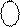
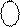
 Очевидно, що у цьому разі
Очевидно, що у цьому разі
 1
1  0
0  0 = 1.
0 = 1.
Тоді згідно з алгоритмом спочатку визначимо ознаку ω за допомогою суматора (1.69) :
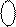
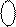
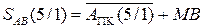 = 0 0010 + 0 0111 = 0 1001.
= 0 0010 + 0 0111 = 0 1001.
 Таким чином маємо
Таким чином маємо 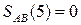 , тому згідно з (1.70) отримаємо:
, тому згідно з (1.70) отримаємо:
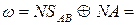 0 + 1 = 1.
0 + 1 = 1.
Отже, МА > MB, і згідно з (1.68) маємо:
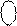
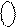
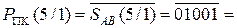 1 0110.
1 0110.
Нехай тепер треба виконати віднімання прямих кодів (А  - В
- В  ) у випадку, коли
) у випадку, коли
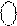 А
А  (5/1) = 1 0011 (NA=1, MA=0011),
(5/1) = 1 0011 (NA=1, MA=0011),
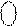 B
B  (5/1) = 1 1011 (NВ=1, MВ=1011).
(5/1) = 1 1011 (NВ=1, MВ=1011).
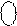
 Очевидно, що у цьому випадку маємо
Очевидно, що у цьому випадку маємо
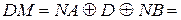 1
1  1
1  1 = 1.
1 = 1.
Тоді згідно з алгоритмом у першому такті потрібно визначити ознаку ω. Для цього отримаємо суму:
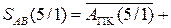 0 МВ(4/1) =
0 МВ(4/1) =
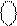
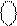
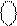
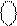
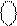
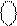 =
= 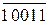 + 0 1011 = 0 1100 + 0 1011 = 1 0111,
+ 0 1011 = 0 1100 + 0 1011 = 1 0111,
де NSAB = 1 , 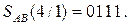
 Таким чином, маємо:
Таким чином, маємо:
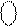
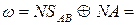 1
1  1 = 0.
1 = 0.
Це означає, що правильний результат необхідно обчислювати за формулою (1.72):
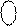
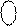
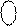
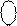
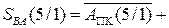 0 МВ(4/1) + 1 = 0 1100 + 0 1011 + 1 = 1 1000,
0 МВ(4/1) + 1 = 0 1100 + 0 1011 + 1 = 1 1000,
де SBA(5) = 1; SBA(4/1) = 1000.
Звідси згідно з (1.73) отримаємо:
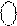
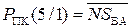
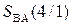 = 0 1000.
= 0 1000.
Можлива структура блока за визначеним алгоритмом 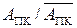 подана на рис.1.29.
подана на рис.1.29.
Схема вміщує:
- суматор SM для обчислення суми модулів чисел;
- суматор SMAB для визначення правильної різниці модулів за умови, коли МА ≥ МВ;
- суматор SMBA для обчислення правильної різниці модулів за умови, коли МА<MB;
- допоміжні схеми для визначення необхідних ознак результату, інвертування кодів та фіксації коректного результату операції.
На завершення можна сказати, що основною перевагою побудованої схеми є потенційно висока швидкодія через те, що обчислення ознак поточної операції і фіксація правильного результату відбувається в пристрої за один такт за будь-яких значень операндів.

Рисунок 1.29,а - Модуль 1 арифметичного пристрою для додавання
і віднімання чисел у прямих кодах за алгоритмом АПК/ 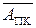
1.2.8 Структура спрощеного арифметичного пристрою для


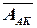
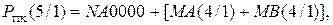 ( 1.62 )
( 1.62 )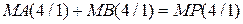 - чотирирозрядний модуль результату у нормальній формі;
- чотирирозрядний модуль результату у нормальній формі;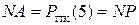 - правильний знак результату за DМ = 0.
- правильний знак результату за DМ = 0.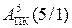 = NA 0000 + MA(4/1),
= NA 0000 + MA(4/1), вираз (1.62) можна подати у вигляді:
вираз (1.62) можна подати у вигляді: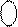
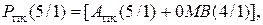 ( 1.63 )
( 1.63 )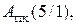
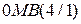 - відповідно п’ятирозрядний прямий код операнда А і п’ятипозиційний код модуля операнда В.
- відповідно п’ятирозрядний прямий код операнда А і п’ятипозиційний код модуля операнда В.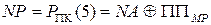 ( 1.64 )
( 1.64 ) NA, якщо МА(4/1)+МВ(4/1) ≤ 15;
NA, якщо МА(4/1)+МВ(4/1) ≤ 15;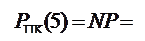
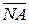 , якщо МА(4/1)+МВ(4/1) ≥ 16, тобто
, якщо МА(4/1)+МВ(4/1) ≥ 16, тобто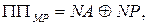 ( 1.65 )
( 1.65 )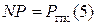 - значення п’ятого розряду повної суми
- значення п’ятого розряду повної суми 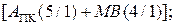
 +В
+В  А
А  B
B 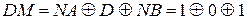 = 0.
= 0.
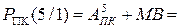 1 0110 + 0 0111 = 1 1101,
1 0110 + 0 0111 = 1 1101,
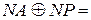 1
1  1 = 0.
1 = 0. А
А  B
B 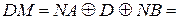 1
1 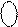
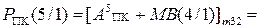 [ 1 1101+ 0 0111]m16 = 0 0100,
[ 1 1101+ 0 0111]m16 = 0 0100,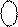 Звідси згідно з (1.65) отримаємо
Звідси згідно з (1.65) отримаємо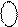 ППМР =
ППМР = 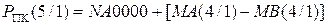 ( 1.66 )
( 1.66 )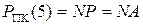 - знак результату за умови ω = 1;
- знак результату за умови ω = 1;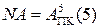 - знак прямого коду числа А.
- знак прямого коду числа А.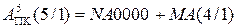
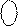
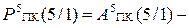 0 МВ(4/1). ( 1.67 )
0 МВ(4/1). ( 1.67 )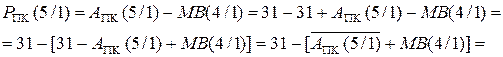
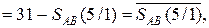 ( 1.68 )
( 1.68 )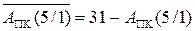 ;
;
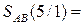 NSAB SAB(4/1) =
NSAB SAB(4/1) = 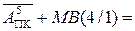
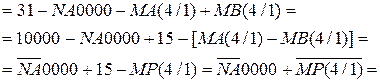
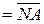
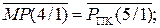
 NA MP(4/1) – прямий код результату за умови, коли МА(4/1) ≥ МВ(4/1);
NA MP(4/1) – прямий код результату за умови, коли МА(4/1) ≥ МВ(4/1);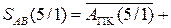 0 МВ(4/1);
0 МВ(4/1);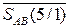 - порозрядна інверсія коду
- порозрядна інверсія коду 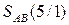 ;
;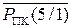 - порозрядна інверсія п’ятирозрядного коду
- порозрядна інверсія п’ятирозрядного коду 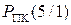 .
.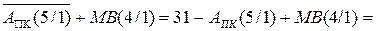
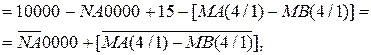
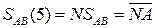 ,
, SAB(5/1) =
SAB(5/1) = 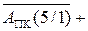 0 МВ(4/1), ( 1.69 )
0 МВ(4/1), ( 1.69 )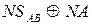 , ( 1.70 )
, ( 1.70 )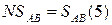 - позначення знакового розряду повної суми операції (1.69).
- позначення знакового розряду повної суми операції (1.69).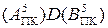 у прямому коді визначається формулою:
у прямому коді визначається формулою: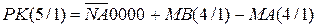 ( 1.71 )
( 1.71 )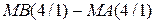 - правильний модуль результату;
- правильний модуль результату;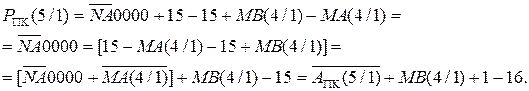
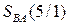 визначити за формулою
визначити за формулою
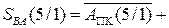 0 МВ(4/1) + 1, ( 1.72 )
0 МВ(4/1) + 1, ( 1.72 )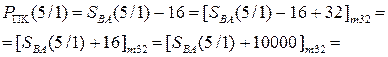
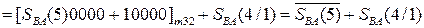 , ( 1.73 )
, ( 1.73 )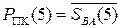 - знак прямого коду результату;
- знак прямого коду результату;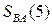 - значення п’ятого розряду суматора (1.72);
- значення п’ятого розряду суматора (1.72);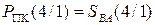 - модуль результату ;
- модуль результату ;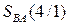 - чотирирозрядний рядок молодших цифр суматора (1.72);
- чотирирозрядний рядок молодших цифр суматора (1.72);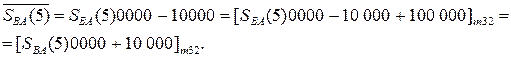
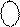 А
А 
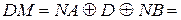 1
1 
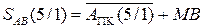 = 0 0010 + 0 0111 = 0 1001.
= 0 0010 + 0 0111 = 0 1001.
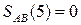 , тому згідно з (1.70) отримаємо:
, тому згідно з (1.70) отримаємо: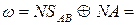 0 + 1 = 1.
0 + 1 = 1.
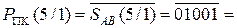 1 0110.
1 0110. А
А  B
B 
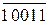 + 0 1011 = 0 1100 + 0 1011 = 1 0111,
+ 0 1011 = 0 1100 + 0 1011 = 1 0111,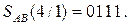
 Таким чином, маємо:
Таким чином, маємо:
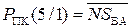
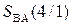 = 0 1000.
= 0 1000.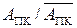 подана на рис.1.29.
подана на рис.1.29.