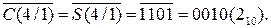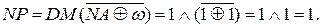МА/ 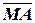
Основним недоліком розглянутої вище структури за алгоритмом МА/ 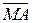 є відносно великі апаратурні витрати. Для мінімізації схеми, очевидно, у пристрої можна застосувати тільки один суматор із динамічним конфігуруванням його інформаційних каналів. Можлива схема такого мінімального операційного блока подана на рис.1.27. Налагоджування суматора на потрібний режим роботи виконується за допомогою сигналів керування СКА і СКНА, за якими до першого входу А суматора через мультиплексор MUXA надходять коди МА/
є відносно великі апаратурні витрати. Для мінімізації схеми, очевидно, у пристрої можна застосувати тільки один суматор із динамічним конфігуруванням його інформаційних каналів. Можлива схема такого мінімального операційного блока подана на рис.1.27. Налагоджування суматора на потрібний режим роботи виконується за допомогою сигналів керування СКА і СКНА, за якими до першого входу А суматора через мультиплексор MUXA надходять коди МА/ 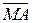 . Формування коду МА відбувається за кодом операції над модулями DМ = 0, а коду
. Формування коду МА відбувається за кодом операції над модулями DМ = 0, а коду 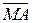 - за ознакою DМ = 1, тобто при відніманні модулів чисел.
- за ознакою DМ = 1, тобто при відніманні модулів чисел.
Якщо СКА = 1, СКНА = 0, СКе(ВХП) = 0, то на виводах суматора утворюється сума модулів (МА+МВ+0) та ознака переповнення ПП (на виводі вихідного переносу суматора ЕS). Шляхом зміни керуючих сигналів забезпечується настроювання суматора на виконання мікрооперації 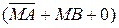 або мікрооперації
або мікрооперації 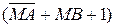 , тобто обчислення правильної різниці модулів відповідно як за умови МА ≥ МВ, так і за умови МВ > МА. При цьому суматор одночасно виконує функції формувача ознаки співвідношення модулів чисел. За мікрооперацією
, тобто обчислення правильної різниці модулів відповідно як за умови МА ≥ МВ, так і за умови МВ > МА. При цьому суматор одночасно виконує функції формувача ознаки співвідношення модулів чисел. За мікрооперацією 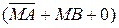 на виводі вихідного переносу суматора ЕS утворюється ознака
на виводі вихідного переносу суматора ЕS утворюється ознака 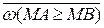 . У випадку, коли
. У випадку, коли 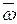 =0, згідно з алгоритмом МА/
=0, згідно з алгоритмом МА/ 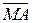 при виконанні мікрооперації
при виконанні мікрооперації 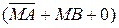 до регістра результату через мультиплексор MUXPP записується інверсне значення кода суми
до регістра результату через мультиплексор MUXPP записується інверсне значення кода суми 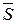 . За станом
. За станом 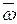 =1 правильна різниця модулів обчислюється за формулою
=1 правильна різниця модулів обчислюється за формулою 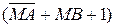 , яка реалізується у наступному такті за керуючими сигналами СКНА = СКе = 1. Таким чином, правильна різниця модулів у мінімальному пристрої за алгоритмом МА/
, яка реалізується у наступному такті за керуючими сигналами СКНА = СКе = 1. Таким чином, правильна різниця модулів у мінімальному пристрої за алгоритмом МА/ 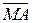 обчислюється за один або два такти. Можлива мікропрограма керуючого автомата мінімального пристрою (рис.1.27) за алгоритмом МА/
обчислюється за один або два такти. Можлива мікропрограма керуючого автомата мінімального пристрою (рис.1.27) за алгоритмом МА/ 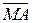 наведена на рис.1.28.
наведена на рис.1.28.
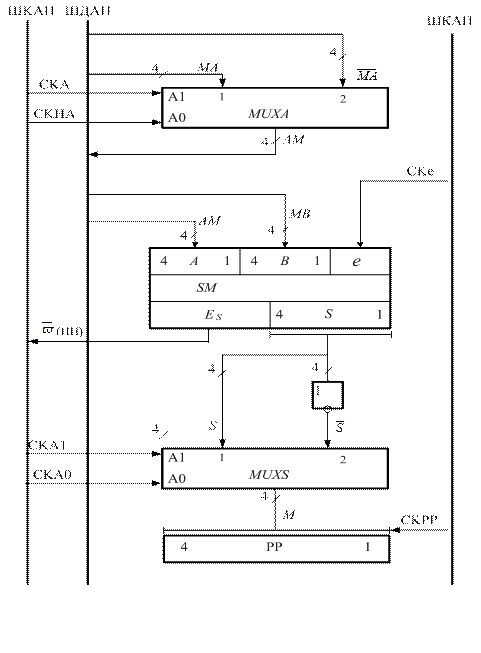
Рисунок 1.27 – Структура спрощеного операційного
пристрою для додавання і віднімання чисел у прямих
кодах за алгоритмом МА/ 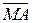
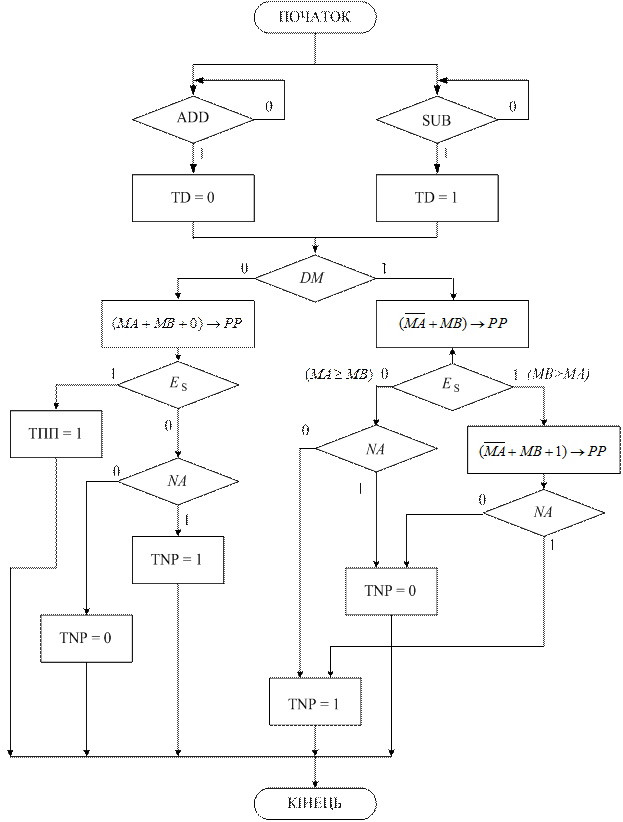
Рисунок 1.28 – Граф змістовної мікропрограми спрощеного
операційного пристрою для додавання і віднімання чисел у
прямих кодах за алгоритмом МА/ 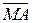
На завершення розглянемо типові приклади, які ілюструють застосування алгоритма МА/ 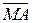 .
.
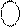
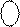 Припустімо, що треба виконати операцію додавання чисел у прямому коді А5ПК + В5ПК (D = 0), причому А5ПК = 0 0111 (NA = 0, MA = 0111), B5ПК= 1 1001 (NB = 1, MB = 1001).
Припустімо, що треба виконати операцію додавання чисел у прямому коді А5ПК + В5ПК (D = 0), причому А5ПК = 0 0111 (NA = 0, MA = 0111), B5ПК= 1 1001 (NB = 1, MB = 1001).
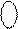
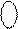
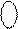 Передусім згідно з алгоритмом в операційному пристрої визначимо код операції над модулями чисел
Передусім згідно з алгоритмом в операційному пристрої визначимо код операції над модулями чисел
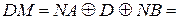 0
0  0
0  1 = 1.
1 = 1.
Далі з урахуванням того, що модулі чисел необхідно віднімати (DМ=1), визначимо ознаку співвідношення модулів ω (МА ≥ МВ). Із цією метою обчислимо код повної суми
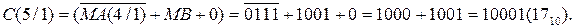
Отже, маємо С(5/1)>16, тому на виході суматора отримаємо ЕS = 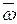 =1. Це означає, що МВ > МА, тому правильну чотирирозрядну різницю модулів МР(4/1) = |МА – МВ| потрібно обчислювати за співвідношенням:
=1. Це означає, що МВ > МА, тому правильну чотирирозрядну різницю модулів МР(4/1) = |МА – МВ| потрібно обчислювати за співвідношенням:
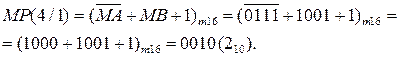
Згідно з алгоритмом (рис.1.28) знак результату NP набуває значення:
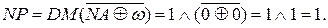
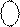 Розглянемо далі операцію віднімання прямих кодів А5ПК і В5ПК (за D=1) за значень аргументів:
Розглянемо далі операцію віднімання прямих кодів А5ПК і В5ПК (за D=1) за значень аргументів:
А5ПК = 1 1001 (NA=1, MA=1001),
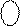 B5ПК = 1 0111 (NB=1, MB=0111).
B5ПК = 1 0111 (NB=1, MB=0111).
Згідно із загальним алгоритмом додавання і віднімання прямих кодів спочатку потрібно визначити ознаку дії над модулями чисел
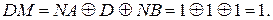
Таким чином, у даному випадку модулі чисел необхідно віднімати, тому передусім визначимо ознаку співвідношення модулів чисел ω. Із цією метою обчислимо повну суму слів:
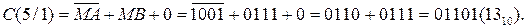
Із урахуванням того, що С(5)=0, на виводі вихідного переносу суматора ЕS = 0, тому 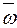 = 0. Таким чином, у даному випадку МА > МВ і правильна різниця МР(4/1) визначається рядком цифр
= 0. Таким чином, у даному випадку МА > МВ і правильна різниця МР(4/1) визначається рядком цифр
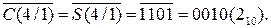
Знак результату згідно з правилами арифметики за цих умов набуває значення:
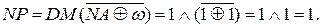
1.2.7 Теоретичні засади та структура арифметичних пристроїв


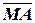
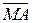 є відносно великі апаратурні витрати. Для мінімізації схеми, очевидно, у пристрої можна застосувати тільки один суматор із динамічним конфігуруванням його інформаційних каналів. Можлива схема такого мінімального операційного блока подана на рис.1.27. Налагоджування суматора на потрібний режим роботи виконується за допомогою сигналів керування СКА і СКНА, за якими до першого входу А суматора через мультиплексор MUXA надходять коди МА/
є відносно великі апаратурні витрати. Для мінімізації схеми, очевидно, у пристрої можна застосувати тільки один суматор із динамічним конфігуруванням його інформаційних каналів. Можлива схема такого мінімального операційного блока подана на рис.1.27. Налагоджування суматора на потрібний режим роботи виконується за допомогою сигналів керування СКА і СКНА, за якими до першого входу А суматора через мультиплексор MUXA надходять коди МА/ 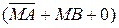 або мікрооперації
або мікрооперації 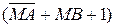 , тобто обчислення правильної різниці модулів відповідно як за умови МА ≥ МВ, так і за умови МВ > МА. При цьому суматор одночасно виконує функції формувача ознаки співвідношення модулів чисел. За мікрооперацією
, тобто обчислення правильної різниці модулів відповідно як за умови МА ≥ МВ, так і за умови МВ > МА. При цьому суматор одночасно виконує функції формувача ознаки співвідношення модулів чисел. За мікрооперацією 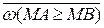 . У випадку, коли
. У випадку, коли 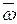 =0, згідно з алгоритмом МА/
=0, згідно з алгоритмом МА/ 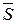 . За станом
. За станом 

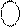
 Припустімо, що треба виконати операцію додавання чисел у прямому коді А5ПК + В5ПК (D = 0), причому А5ПК = 0 0111 (NA = 0, MA = 0111), B5ПК= 1 1001 (NB = 1, MB = 1001).
Припустімо, що треба виконати операцію додавання чисел у прямому коді А5ПК + В5ПК (D = 0), причому А5ПК = 0 0111 (NA = 0, MA = 0111), B5ПК= 1 1001 (NB = 1, MB = 1001).
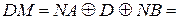 0
0  0
0 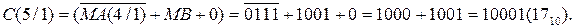
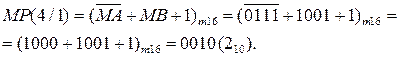
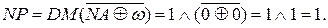
 Розглянемо далі операцію віднімання прямих кодів А5ПК і В5ПК (за D=1) за значень аргументів:
Розглянемо далі операцію віднімання прямих кодів А5ПК і В5ПК (за D=1) за значень аргументів: B5ПК = 1 0111 (NB=1, MB=0111).
B5ПК = 1 0111 (NB=1, MB=0111).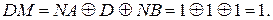
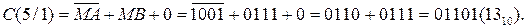
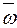 = 0. Таким чином, у даному випадку МА > МВ і правильна різниця МР(4/1) визначається рядком цифр
= 0. Таким чином, у даному випадку МА > МВ і правильна різниця МР(4/1) визначається рядком цифр