Основним недоліком розглянутої структури (рис.1.23) є великі апаратні витрати в операційному блоці. Для зменшення апаратних витрат у мінімальній схемі на основі доповнення модулів чисел для додадання і віднімання модулів чисел застосовується один суматор (рис.1.24), за допомогою якого виконується як додавання, так і непряме віднімання модулів чисел. Налагоджування суматора на відповідний режим роботи у схемі виконується за допомогою сигналів керування СКА (СКНА) і СКВ (СКНВ), за яких до інформаційних входів А і В суматора подаються модулі слів або їх порозрядна інверсія. Із цією метою схема операційного пристрою доповнена мультиплексорами MUXA і MUXB, які прибудовані відповідно до входів А і В суматора. Входи керування мультиплексорів А1 і А0 (А1А0 – адреса інформаційних входів мультиплексорів) налагоджуються сигналами керування (СК) місцевого керуючого пристрою відповідно СКА (СКНА) і СКВ (СКНВ). Згідно з алгоритмом, якщо СКА = 1, СКВ = 1 та СКе = 0 (ВХП=0), то на виводах суматора утворюються коди суми модулів чисел (МА + МВ) та сигнал переповнення ПП розрядної сітки (на виводі вихідного переносу суматора). Шляхом зміни комбінації сигналів керування суматор налагоджується на виконання операцій непрямого віднімання модулів 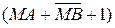 або
або 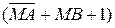 і, таким чином, обчислюється правильна різниця модулів за будь-яких значень модулів МА і МВ. При цьому вихідний сигнал переносу ЕS суматора являє собою багатофункціональний вивід. При виконанні операції додавання модулів МА і МВ (за DМ = 0) на виводі ЕS суматора формується сигнал переповнення вихідного коду S(4/1) суматора. При відніманні модулів чисел (МА – МВ), яке відбувається за DМ=1 шляхом підсумовування кодів
і, таким чином, обчислюється правильна різниця модулів за будь-яких значень модулів МА і МВ. При цьому вихідний сигнал переносу ЕS суматора являє собою багатофункціональний вивід. При виконанні операції додавання модулів МА і МВ (за DМ = 0) на виводі ЕS суматора формується сигнал переповнення вихідного коду S(4/1) суматора. При відніманні модулів чисел (МА – МВ), яке відбувається за DМ=1 шляхом підсумовування кодів 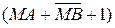 , вивід ЕS суматора являє собою ознаку відношення модулів ω(МА ≥ МВ). При цьому ЕS = ω тільки у тому разі, якщо на інформаційних входах суматора формуються коди
, вивід ЕS суматора являє собою ознаку відношення модулів ω(МА ≥ МВ). При цьому ЕS = ω тільки у тому разі, якщо на інформаційних входах суматора формуються коди 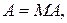
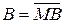 і ВХП= 1, тобто за активних значень сигналів керування СКА=СКНВ=Ске = 1.
і ВХП= 1, тобто за активних значень сигналів керування СКА=СКНВ=Ске = 1.
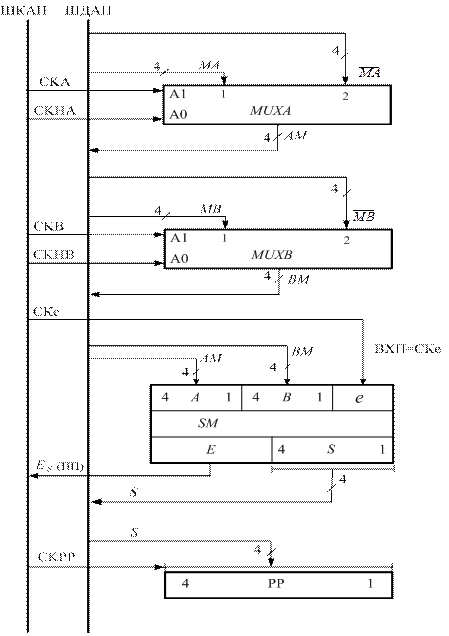
Рисунок 1.24 – Структура спрощеного операційного блока
для додавання і віднімання чисел у прямих кодах на основі
доповнення модулів чисел
За сигналом ЕS = ω = 0 при виконанні мікрооперації 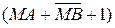 код суми не являє собою правильну різницю модулів чисел МА і МВ. Правильне значення різниці модулів МА і МВ у цьому випадку визначається у другому такті шляхом виконання мікрооперації
код суми не являє собою правильну різницю модулів чисел МА і МВ. Правильне значення різниці модулів МА і МВ у цьому випадку визначається у другому такті шляхом виконання мікрооперації 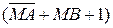 . Таким чином, при виконанні операції віднімання модулів чисел розрахунок правильної різниці модулів МР = |МА - МВ| загалом здійснюється за два такти. Це зумовлено тим, що за умови МВ > МА у першому такті не визначається правильна різниця модулів. Для обчислення правильноїрізниці чисел у цьому разі повинен бути ще один такт для виконання дії (МВ – МА) за допомогою мікрооперації РР=
. Таким чином, при виконанні операції віднімання модулів чисел розрахунок правильної різниці модулів МР = |МА - МВ| загалом здійснюється за два такти. Це зумовлено тим, що за умови МВ > МА у першому такті не визначається правильна різниця модулів. Для обчислення правильноїрізниці чисел у цьому разі повинен бути ще один такт для виконання дії (МВ – МА) за допомогою мікрооперації РР= 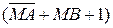 . Для ілюстрації зазначених функціональних особливостей операційного блока на рис.1.25 подано змістовну мікропро-граму мінімального операційного пристрою.
. Для ілюстрації зазначених функціональних особливостей операційного блока на рис.1.25 подано змістовну мікропро-граму мінімального операційного пристрою.
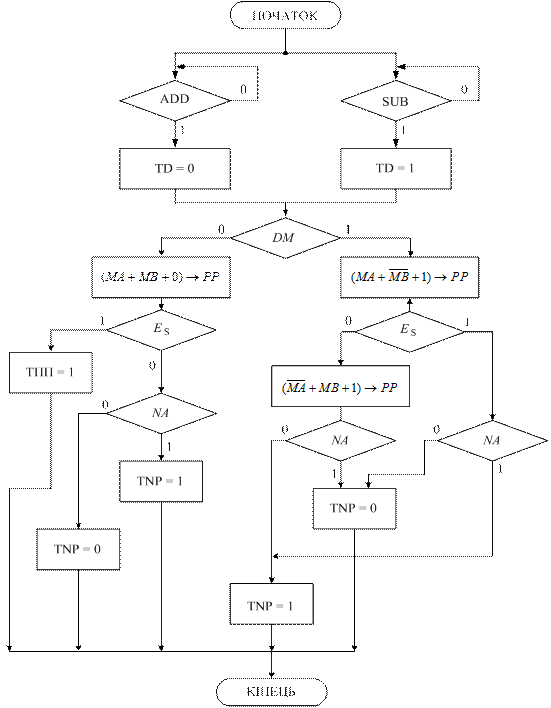
Рисунок 1.25 - Граф змістовної мікропрограми спрощеного
арифметичного пристрою для додавання і віднімання чисел у
прямих кодах на основі доповнення модулів чисел (рис.1.24)
Як випливає з наведеного, як первинна (рис.1.23), так і мінімальна (рис.1.24) схема операційного блока мають певні недоліки і переваги і кожна варта уваги. В первинній схемі за будь-яких значень операндів модуль результату обчислюється за один такт завдяки тому, що у блоці одночасно (паралельно) виконуються операції МА + МВ, МА – МВ і МВ – МА, тобто обчислюється правильний результат за будь-яких обставин. У спрощеному блоці апаратні витрати зменшені в три рази, але час виконання операції в найгіршому випадку дорівнює двом тактам.
1.2.5 Структура канонічного арифметичних пристроїв для додавання
і віднімання чисел у прямих кодах за алгоритмом МА/ 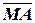
Згідно з правилами арифметики за кодом операції над модулями DМ =1 (тобто при обчисленні результату шляхом віднімання модулів чисел) і за умови МА ≥ МВ правильна різниця модулів, наприклад, за чотирирозрядним форматом визначається за співвідношенням:
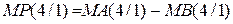 , ( 1.55 )
, ( 1.55 )
де МР(4/1) – різниця чотирипозиційних модулів МА(4/1) і МВ(4/1) п’ятирозрядних прямих кодів А5ПК і В5ПК.
Щоб уникнути операції прямого віднімання модулів рівняння (1.55) перетворимо наступним чином:
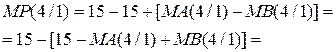
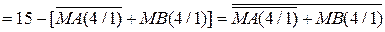 . ( 1.56 )
. ( 1.56 )
Таким чином, для обчислення різниці (1.55) згідно з (1.56) необхідно виконати дві мікрооперації:
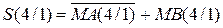 ; ( 1.57 )
; ( 1.57 )
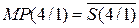 . ( 1.58 )
. ( 1.58 )
Зазначимо, що згідно з (1.56) функція
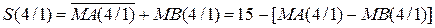 ,
,
тобто за ознакою відношення модулів ω (МА ≥ МВ) = 1 код повної суми набуває значення S(4/1) ≤ 15.
Отже, код повної суми SAB суматора SMAB (рис.1.26) не перевищує чотирьох біт, тому вихідний сигнал переносу суматора SMAB за умови ω(МА ≥ МВ) =1 приймає нульове значення. Звідси маємо
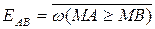 . ( 1.59 )
. ( 1.59 )
За умови, коли МА < МВ правильна різниця модулів визначається формулою:
МР(4/1) = МВ(4/1) – МА(4/1). ( 1.60 )
Щоб уникнути операції прямого віднімання модулів вираз (1.60) запишемо у вигляді:
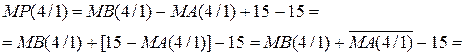
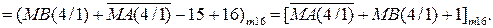 ( 1.61 )
( 1.61 )
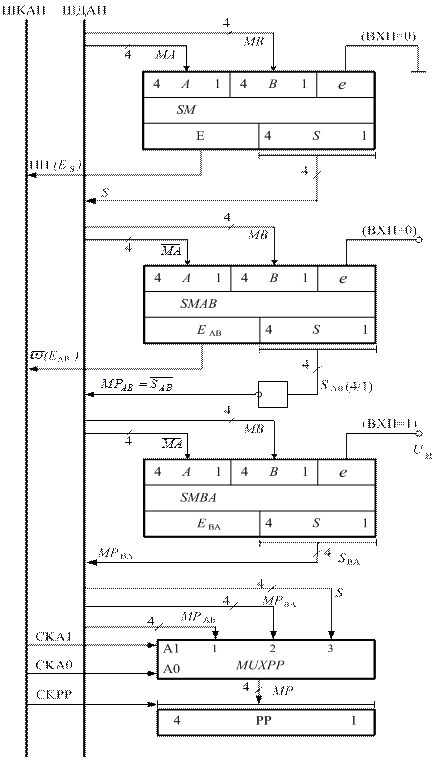
Рисунок 1.26 – Структура арифметичного пристрою для додавання
і віднімання чисел у прямих кодах за алгоритмом МА/ 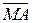
Це означає, що за умови ω (МВ > МА) = 0 різниця модулів чисел (МВ - МА), власне, еквівалентна цифровому рядку суми SBA(4/1) суматора SMBA (рис.1.26), який налагоджено на виконання операції:
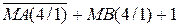 .
.
Згідно з наведених міркувань для обчислення суми і різниці модулів за алгоритмом МА/ 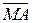 на рис.1.26 побудована можлива структурна схема арифметичного пристрою, яка вміщує:
на рис.1.26 побудована можлива структурна схема арифметичного пристрою, яка вміщує:
- суматор SM для формування суми модулів (МА + МВ) і ознаки переповнення суматора ( ПП = ЕS );
- суматор SMAB і інвертор 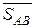 для формування правильної різниці модулів чисел за умови МА ≥ МВ та інверсного значення ознаки відношення модулів (
для формування правильної різниці модулів чисел за умови МА ≥ МВ та інверсного значення ознаки відношення модулів ( 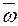 );
);
- суматор SMBA для формування коректної різниці модулів чисел за умови МВ > МА;
- мультиплексор MUXPP для комутації правильного результату обчислень до інформаційних входів регістра результату;
- допоміжний сигнал напруги високого рівня Uн для формування одиниці на контакті вхідного перенесення суматора SMBA.
Операційні пристрої SM, SMAB, SMBA у схемі спрацьовують паралельно, тому коректний результат та ознаки операцій у побудованому арифметич-ному пристрої за будь-яких значень операндів обчислюються за один такт.
1.2.6 Структура спрощеного арифметичного пристрою для


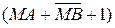 або
або 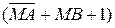 і, таким чином, обчислюється правильна різниця модулів за будь-яких значень модулів МА і МВ. При цьому вихідний сигнал переносу ЕS суматора являє собою багатофункціональний вивід. При виконанні операції додавання модулів МА і МВ (за DМ = 0) на виводі ЕS суматора формується сигнал переповнення вихідного коду S(4/1) суматора. При відніманні модулів чисел (МА – МВ), яке відбувається за DМ=1 шляхом підсумовування кодів
і, таким чином, обчислюється правильна різниця модулів за будь-яких значень модулів МА і МВ. При цьому вихідний сигнал переносу ЕS суматора являє собою багатофункціональний вивід. При виконанні операції додавання модулів МА і МВ (за DМ = 0) на виводі ЕS суматора формується сигнал переповнення вихідного коду S(4/1) суматора. При відніманні модулів чисел (МА – МВ), яке відбувається за DМ=1 шляхом підсумовування кодів 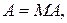
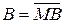 і ВХП= 1, тобто за активних значень сигналів керування СКА=СКНВ=Ске = 1.
і ВХП= 1, тобто за активних значень сигналів керування СКА=СКНВ=Ске = 1.
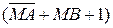 . Таким чином, при виконанні операції віднімання модулів чисел розрахунок правильної різниці модулів МР = |МА - МВ| загалом здійснюється за два такти. Це зумовлено тим, що за умови МВ > МА у першому такті не визначається правильна різниця модулів. Для обчислення правильноїрізниці чисел у цьому разі повинен бути ще один такт для виконання дії (МВ – МА) за допомогою мікрооперації РР=
. Таким чином, при виконанні операції віднімання модулів чисел розрахунок правильної різниці модулів МР = |МА - МВ| загалом здійснюється за два такти. Це зумовлено тим, що за умови МВ > МА у першому такті не визначається правильна різниця модулів. Для обчислення правильноїрізниці чисел у цьому разі повинен бути ще один такт для виконання дії (МВ – МА) за допомогою мікрооперації РР= 
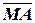
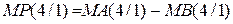 , ( 1.55 )
, ( 1.55 )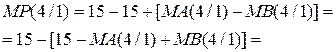
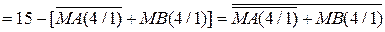 . ( 1.56 )
. ( 1.56 )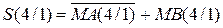 ; ( 1.57 )
; ( 1.57 )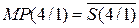 . ( 1.58 )
. ( 1.58 )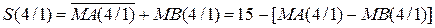 ,
,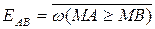 . ( 1.59 )
. ( 1.59 )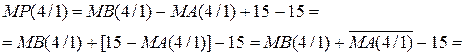
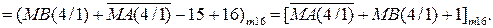 ( 1.61 )
( 1.61 )
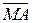
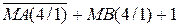 .
.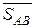 для формування правильної різниці модулів чисел за умови МА ≥ МВ та інверсного значення ознаки відношення модулів (
для формування правильної різниці модулів чисел за умови МА ≥ МВ та інверсного значення ознаки відношення модулів ( 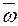 );
);