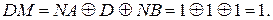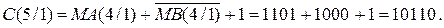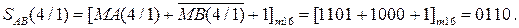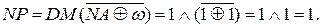Операція додавання і віднімання чисел у прямих кодах полягає в тому, що спочатку визначається дія над модулями чисел (DМ), а потім формується модуль результату (МР) і код знака результату (NP). Припустімо, що модуль результату МР за кодом DМ = 0 визначається сумою модулів чисел МА + МВ, а за кодом DМ = 1 – різницею модулів чисел |MA – MB| .
Для утворення суми і додатної різниці модулів в обчислювачі, який подано на рис. 1.23, пристосовані суматори. До складу обчислювача входять:
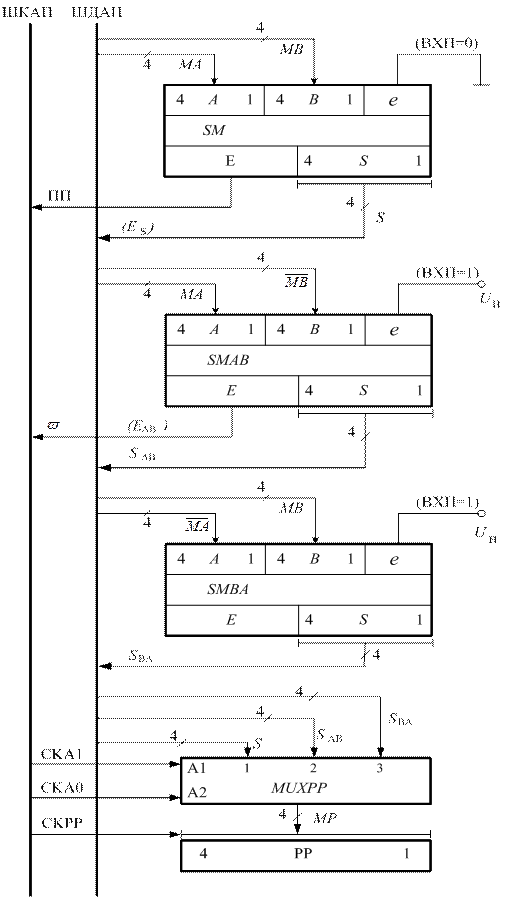
Рисунок 1.23 – Структура арифметичного пристрою для додавання і
віднімання чисел у прямих кодах на основі доповнення модулів операндів
- суматор SM для утворення суми модулів МА + МВ;
- віднімач на основі суматора SMАВ для обчислення різниці модулів МР у тому разі, коли МА ≥ МВ;
- віднімач на основі суматора SMВА для формування різниці модулів МР у тому випадку, коли МВ>МА;
- мультиплексор MUXPP для комутації виходів операційних арифметичних вузлів SM, SMАВ та SMВА до інформаційних входів регістра модуля результату РР згідно з кодом операції над модулями чисел DМ та ознакою відношення модулів чисел ω;
- сигнали керування СКА1, СКА2 і СКРР для налагодження необхідної адреси мультиплексора MUXPP та дозволяючого входу регістра РР;
- ознаку переповнення (ПП) розрядної сітки (довжини) регістра результату;
- сигнал верхнього рівня напруги Uн для формування логічних одиниць на виводах вхідного переносу ВХП АВ та ВХП ВА віднімачів на основі SMАВ та SMВА.
Операція додавання чотирирозрядних модулів MА(4/1) і MВ(4/1) (за DМ=0) в обчислювачі (рис.1.23) виконується типовим чотирирозрядним суматором SM(4/1) за формулами:
S(4/1) = [MA(4/1) + MB(4/1)]m16 ; ( 1.38 )
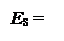
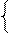 0, якщо MA(4/1) + MB(4/1) ≤ 15; ( 1.39 )
0, якщо MA(4/1) + MB(4/1) ≤ 15; ( 1.39 )
1, якщо MA(4/1) + MB(4/1) ≥16, ( 1.40 )
де MA(4/1), MB(4/1), S(4/1) –чотирирозрядна низка двійкових розрядів від-повідно на першому А і другому В входах та на виході S суматору SM;
ES - позначення вихідного переносу чотирирозрядного суматора з ваговим коефіцієнтом 16, тобто стан п’ятого розряду повної суми чотирирозрядних кодів на інформаційних входах А і В суматора.
Згідно з (1.40) за сигналом ES = 1 (рис.1.23) повна сума модулів чисел (МА+МВ) більша 16, тобто у цьому випадку виникає переповнення чотири-розрядної сітки (довжини) вихідного чотирирозрядного коду S(4/1) суматора SM. Таким чином, вихідне перенесення ES обчислювача, поданого на рис.1.23, являє собою сигнал переповнення результату за кодом операції над модулями DМ=0(+). За наявністю переповнення (ПП) результат не фіксується у регістрі результату РР і в центральному пристрої керування комп’ютера (ЦПК) тригер переповнення перемикається в одиницю.
Операція прямого віднімання чотирирозрядних модулів MA(4/1) і MB(4/1) в обчислювачі (рис.1.23) замінюється складанням цифрового ряду більшого модуля і коду доповнення модуля меншого операнда. Для обчис-лення правильної різниці модулів зазначеним способом за умови MA ≥ MB в обчислювачі використовується SMАВ, а за умови MB > MA – SMВА (рис.1.23).
У чотирирозрядному SMВА різниця модулів розраховується наступним чином:
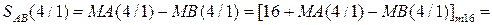

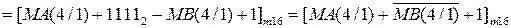 ( 1.41 )
( 1.41 )
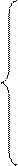 1, якщо
1, якщо 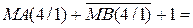
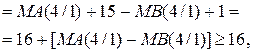 ( 1.42 )
( 1.42 )
EАВ = тобто за умови MA ≥ MB;
0, якщо 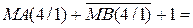
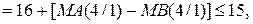 ( 1.43 )
( 1.43 )
тобто за умови MB > MA,
де SAB(4/1) – чотирирозрядна низка двійкових цифрових розрядів коду суми суматора SMАВ;
16(24) – вагова характеристика двійкового розряду зліва від найстаршого розряду суми SAB(4/1) суматора;
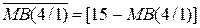 - порозрядна інверсія чотирирозрядного слова МВ(4/1);
- порозрядна інверсія чотирирозрядного слова МВ(4/1);
[ 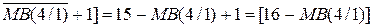 - ( 1.44 )
- ( 1.44 )
- доповнення чотирипозиційного модуля МВ(4/1) до 16;
-[ 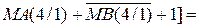 СAB(5/1) - ( 1.45 )
СAB(5/1) - ( 1.45 )
- повна п’ятипозиційна сума чотирирозрядних слів МА(4/1), МВ(4/1) та сигнала перенесення в наймолодший розряд суматора SMАВ;
EАВ – позначення вихідного перенесення суматора SMАВ, яке згідно з (1.42), (1.43) та (1.45) визначає ознаку відношення модулів МА і МВ:
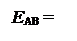
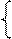 1, якщо МА ≥ МВ (С(5)=1); ( 1.46 )
1, якщо МА ≥ МВ (С(5)=1); ( 1.46 )
0, якщо МВ > МА (С(5)=0). ( 1.47 )
У разі, коли МВ(4/1)>МА(4/1), правильна додатна різниця модулів обчислюється суматором SBA (рис.1.23) за формулами:
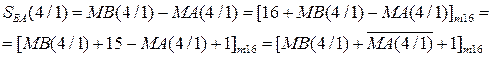 ( 1.48 )
( 1.48 )
 1, якщо
1, якщо 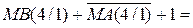
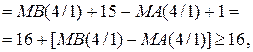 ( 1.49 )
( 1.49 )
EВА = тобто за умови MB ≥ MA;
0, якщо 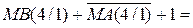
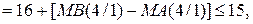 ( 1.50 )
( 1.50 )
тобто за умови MA > MB,
де SBA(4/1) – чотирирозрядний рядок двійкових розрядів на виводах S суматора SMВА;
16(24) – вагова характеристика двійкового розряду зліва від найстаршо-го розряду суми SBA (4/1) суматора;
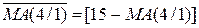 - порозрядна інверсія чотирипозиційного слова МА(4/1);
- порозрядна інверсія чотирипозиційного слова МА(4/1);
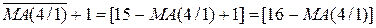 - ( 1.51 )
- ( 1.51 )
- доповнення чотирирозрядного цілого безвід’ємного коду МА(4/1) до 16;
-[ 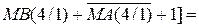 СBA (5/1) - ( 1.52 )
СBA (5/1) - ( 1.52 )
- повна сума чотирирозрядних слів МВ(4/1), 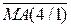 та сигнала перенесення в наймолодший розряд суматора SMВА;
та сигнала перенесення в наймолодший розряд суматора SMВА;
EВА – позначення вихідного перенесення суматора SMВА, яке згідно з (1.49) визначає ознаку відношення модулів чисел:
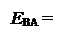
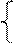 1, якщо МВ ≥ МА; ( 1.53 )
1, якщо МВ ≥ МА; ( 1.53 )
0, якщо МВ < МА. ( 1.54 )
Таким чином, з наведених вище міркувань випливає, що сигнал EАВ суматора SMАВ (рис.1.23) тотожний змінній ω в операційному пристрої на основі віднімачів, тобто визначає ознаку співвідношення модулів чисел. Тому у випадку, коли ЕАВ = ω = 1, за кодом операції над модулями DМ = 1 необхідно фіксувати двійковий код SAB(4/1), а за умови ЕАВ=ω= 0 – двійковий код SBA(4/1).
На завершення розглянемо застосування цього алгоритму на деяких типових прикладах.
 Припустімо, що треба виконати операцію додавання чисел у прямих кодах А5ПК + В5ПК, де А5ПК = 0 1011 (NA = 0, MA = 1011), В5ПК = 1 1101 (NB = 1, MB = 1101).
Припустімо, що треба виконати операцію додавання чисел у прямих кодах А5ПК + В5ПК, де А5ПК = 0 1011 (NA = 0, MA = 1011), В5ПК = 1 1101 (NB = 1, MB = 1101).
Передусім, згідно з алгоритмом в операційному пристрої визначається код операції над модулями чисел за співвідношенням:
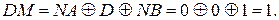
Далі з урахуванням того, що модулі необхідно віднімати, визначається ознака співвідношення модулів ЕАВ шляхом обчислення повної суми С(5/1) на виході суматора SMАВ :
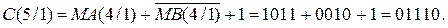
Із урахуванням того, що С(5/1) < 16, маємо С(5) = ЕАВ = 0. Це означає, що у даному випадку МВ > МА, тобто правильна різниця модулів | МА - МВ | формується суматором SMВА, в якому результат визначається наступним чином:
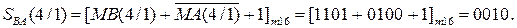
Знак результату у цьому випадку (за DМ = 1) набуває значення:
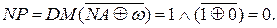
 Розглянемо далі операцію віднімання прямих кодів А5ПК - В5ПК (за D=1). При цьому застосуємо такі дані:
Розглянемо далі операцію віднімання прямих кодів А5ПК - В5ПК (за D=1). При цьому застосуємо такі дані:
А5ПК = 1 1101 ( NA = 1, MA = 1101);
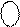 В5ПК = 1 0111( NB = 1, MB = 0111).
В5ПК = 1 0111( NB = 1, MB = 0111).
Із урахуванням коду операції Dспочатку визначимо код операції над модулями чисел:
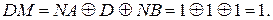
Таким чином, модулі чисел необхідно віднімати, тому далі за алгоритмом визначимо ознаку співвідношення модулів ЕАВ = ω. З цією метою обчислимо повну суму С на виході SMАВ :
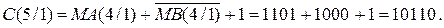
Із урахуванням того, що сума С(5/1) > 16, маємо ЕАВ = 1. Це означає, що у даному випадку МА > МВ. Як було зауважено, правильна різниця модулів при цьому створюється на виходах суматора SMАВ за співвідношенням:
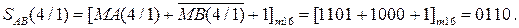
Знак результату NP за даних аргументів набуває значення:
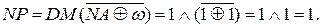
1.2.4 Алгоритми та структура спрощеного арифметичного



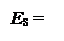
 0, якщо MA(4/1) + MB(4/1) ≤ 15; ( 1.39 )
0, якщо MA(4/1) + MB(4/1) ≤ 15; ( 1.39 )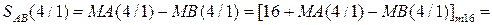

 ( 1.41 )
( 1.41 ) 1, якщо
1, якщо 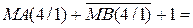
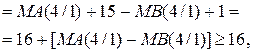 ( 1.42 )
( 1.42 )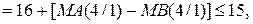 ( 1.43 )
( 1.43 )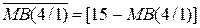 - порозрядна інверсія чотирирозрядного слова МВ(4/1);
- порозрядна інверсія чотирирозрядного слова МВ(4/1);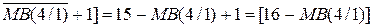 - ( 1.44 )
- ( 1.44 )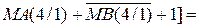 СAB(5/1) - ( 1.45 )
СAB(5/1) - ( 1.45 )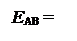
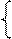 1, якщо МА ≥ МВ (С(5)=1); ( 1.46 )
1, якщо МА ≥ МВ (С(5)=1); ( 1.46 )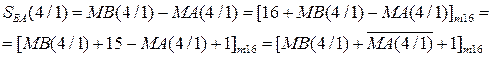 ( 1.48 )
( 1.48 )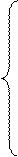 1, якщо
1, якщо 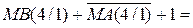
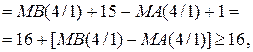 ( 1.49 )
( 1.49 )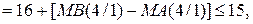 ( 1.50 )
( 1.50 )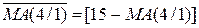 - порозрядна інверсія чотирипозиційного слова МА(4/1);
- порозрядна інверсія чотирипозиційного слова МА(4/1);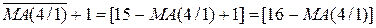 - ( 1.51 )
- ( 1.51 )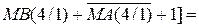 СBA (5/1) - ( 1.52 )
СBA (5/1) - ( 1.52 )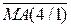 та сигнала перенесення в наймолодший розряд суматора SMВА;
та сигнала перенесення в наймолодший розряд суматора SMВА;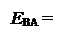
 1, якщо МВ ≥ МА; ( 1.53 )
1, якщо МВ ≥ МА; ( 1.53 )
 Припустімо, що треба виконати операцію додавання чисел у прямих кодах А5ПК + В5ПК, де А5ПК = 0 1011 (NA = 0, MA = 1011), В5ПК = 1 1101 (NB = 1, MB = 1101).
Припустімо, що треба виконати операцію додавання чисел у прямих кодах А5ПК + В5ПК, де А5ПК = 0 1011 (NA = 0, MA = 1011), В5ПК = 1 1101 (NB = 1, MB = 1101).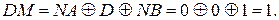
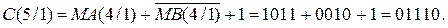
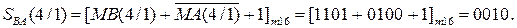
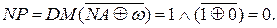
 Розглянемо далі операцію віднімання прямих кодів А5ПК - В5ПК (за D=1). При цьому застосуємо такі дані:
Розглянемо далі операцію віднімання прямих кодів А5ПК - В5ПК (за D=1). При цьому застосуємо такі дані: В5ПК = 1 0111( NB = 1, MB = 0111).
В5ПК = 1 0111( NB = 1, MB = 0111).