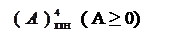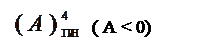Зміщений, наприклад, чотирипозиційний код з позитивним нулем цілих чисел А із знаком визначається співвідношенням:
( А )4ПН = 810 + А , ( 1.17 )
де 410 – довжина розрядної сітки машинного коду з позитивним нулем (ХХХХ);
810 = 2(4-1) – параметр відображення (зміщення) коду з позитивним нулем за чотирипозиційним форматом.
Із “арифметичного” виразу (1.17) випливає область визначення чотири-позиційного зміщеного коду з позитивним нулем:
А = (А ) 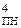 - 810 = ( 0 ¸ 1510) – 810 = (- 810) ¸ (+ 710). ( 1.18 )
- 810 = ( 0 ¸ 1510) – 810 = (- 810) ¸ (+ 710). ( 1.18 )
У графічній формі функцію (1.17) у проміжку її визначення подано на рис. 1.12.
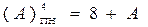
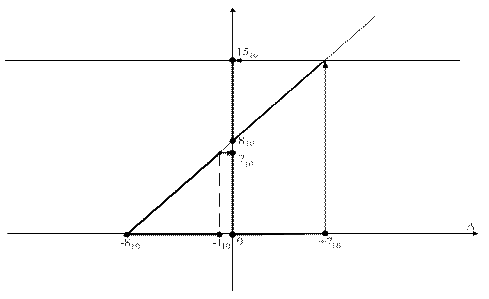
Рисунок 1.12 – Графічна інтерпретація подання чотирипозиційними
кодами з позитивним нулем чисел А із знаком
Розглянемо типові приклади перетворення цілих чисел із знаком у зміщений код з позитивним нулем на основі “арифметичного” виразу (1.17).
Нехай А = - 1012 (-510 ). Тоді згідно з ( 1.17 ) маємо:
 (А )
(А ) 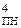 = (810 + А)4 = [ 810 + (- 510)]4 = (310)4 = 0 0112.
= (810 + А)4 = [ 810 + (- 510)]4 = (310)4 = 0 0112.
Нехай тепер В = + 1102 ( + 610 ). Тоді згідно з ( 1.17 ) отримаємо:
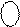 (В )
(В ) 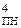 = (810 + В )4 = [ 810 + (+ 610)]4 = (1410)4 = 1 1102.
= (810 + В )4 = [ 810 + (+ 610)]4 = (1410)4 = 1 1102.
На основі “арифметичного” виразу функції (1.17) визначимо “логічний” алгоритм утворення зміщеного коду з позитивним нулем:
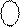 (А )
(А ) 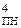 (+ 010 ≤ А ≤ (+ 710 ) = (810 + А)4 =
(+ 010 ≤ А ≤ (+ 710 ) = (810 + А)4 =
= (10002 + | А |3 )4 = 1 | А |3 ; ( 1.19 ) (А ) 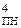 (- 10002 ≤ А ≤ (- 00012 ) = (810 + А)4 =
(- 10002 ≤ А ≤ (- 00012 ) = (810 + А)4 =
= (1610 - | А |4 + 810)m16 = [1510 - | А |4 + 1 + 810]m16 =
= [ 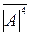 + 1 + 810 ]m16 = [
+ 1 + 810 ]m16 = [ 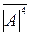 + 1 + 10002] m16 . ( 1.20 )
+ 1 + 10002] m16 . ( 1.20 )
де 1× 23 = 810 = 23 – вага старшого (знакового) розряду функції (1.17).
Розглянемо приклади перетворення чисел із знаком у зміщений код з позитивним нулем на основі “логічних” алгоритмів ( 1.19 ) і ( 1.20 ).
Нехай А = - 0100 (- 410). Тоді згідно з (1.20), машинне зображення чисел А у коді з позитивним нулем буде мати вигляд:
(А )4ПН = [ 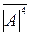 + 1 + 810 ]m16 = (
+ 1 + 810 ]m16 = ( 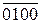 + 1 + 1000 )m16 =
+ 1 + 1000 )m16 =
= (1011+1+1000)m16 = ( 1100+1000 )m16 =

1100
1000 




 ( 1 0100 )m16 = 0 100 .
( 1 0100 )m16 = 0 100 .
Нехай тепер В = + 1102 (+ 610). Тоді згідно з (1.19) машинне зображення чисел В із знаком у зміщеному коді з позитивним нулем буде мати інший вигляд:
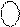
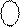 (В )
(В ) 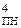 = 1 | В |3 = 1 1102. ( 1.21 )
= 1 | В |3 = 1 1102. ( 1.21 )
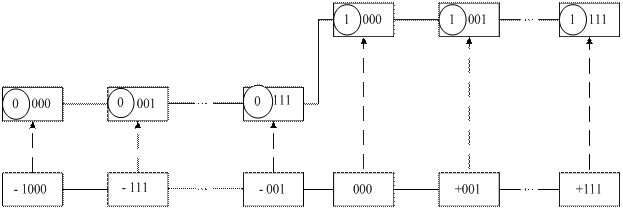
Приклади машинного зображення чисел А із знаком у зміщеному коді з позитивним нулем для області визначення функції ( 1.17 ) подано на рис.1.13.
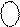
 Із рисунка випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А)
Із рисунка випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А) 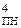 (крайній зліва розряд коду (А )
(крайній зліва розряд коду (А ) 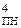 ), а множина від’ємних чисел А – цифрою 0 у знаковому розряді. Зазначимо, що нульове значення оригіналу А (А = 0) відображається у знаковому розряді (А)
), а множина від’ємних чисел А – цифрою 0 у знаковому розряді. Зазначимо, що нульове значення оригіналу А (А = 0) відображається у знаковому розряді (А) 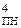 двійковою цифрою 1 , тобто як додатне ціле число (+000). Таким чином, числова множина ( 1 000) ¸ ( 1 111) функції (А)
двійковою цифрою 1 , тобто як додатне ціле число (+000). Таким чином, числова множина ( 1 000) ¸ ( 1 111) функції (А) 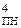 відображає множину додатних двійкових чисел між (+000) і (+111), а числова множина ( 0 000) ¸ ( 0 111) функції (А)
відображає множину додатних двійкових чисел між (+000) і (+111), а числова множина ( 0 000) ¸ ( 0 111) функції (А) 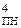 – множину від’ємних чисел у проміжку між (-1000) і (- 0001).
– множину від’ємних чисел у проміжку між (-1000) і (- 0001).
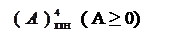
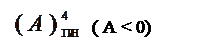
A < 0 A ≥ 0
Рисунок 1.13 – Приклади подання цілих чисел А у проміжку між (-810) і (+710) чотирипозиційними кодами з позитивним нулем


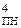 - 810 = ( 0 ¸ 1510) – 810 = (- 810) ¸ (+ 710). ( 1.18 )
- 810 = ( 0 ¸ 1510) – 810 = (- 810) ¸ (+ 710). ( 1.18 )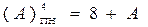

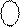 (А )
(А ) 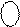 (В )
(В ) 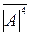 + 1 + 810 ]m16 = [
+ 1 + 810 ]m16 = [ 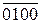 + 1 + 1000 )m16 =
+ 1 + 1000 )m16 =




 ( 1 0100 )m16 = 0 100 .
( 1 0100 )m16 = 0 100 .
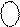
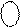
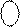 Із рисунка випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А)
Із рисунка випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А)