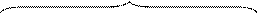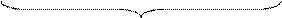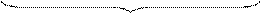У загальному випадку обернений код (ОК) цілих чисел А із знаком можна пов’язати із звичайним зображенням чисел А наступним співвідношенням:
А 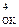 = (1510 + А ) m15, ( 1.10 )
= (1510 + А ) m15, ( 1.10 )
де А  – чотирипозиційний формат (ХХХХ,) оберненого коду чисел А із знаком;
– чотирипозиційний формат (ХХХХ,) оберненого коду чисел А із знаком;
15 = (2410 – 1) – параметр відображення (зміщення) оберненого чотирипозиційного коду;
(1510 + А)m15 – неподільна чотирипозиційна остача ділення безвід’ємних зміщених кодів (15+ А) на 15;
4 – довжина розрядної сітки машинного зображення оберненого коду.
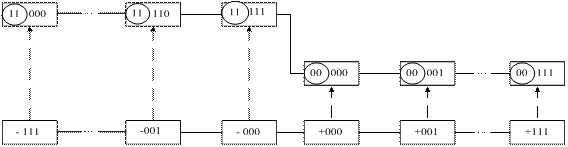
Очевидно, що залежність (1.10) являє собою періодичну функцію з періодом Т=±1510, ±3010 і т.д., тобто є неоднозначною. Однозначність функції (1.10) протягом основного періоду Т=±1510 існує тільки у скороченому інтервалі зміни аргументу А між (-710) і (+710), який може бути визначеним як зона повної однозначності між числом та його машинним зображенням (рис.1.8). У цій зоні (рис.1.8) функції (1.10) кожному додатному числу А у проміжку між (+010) і (+710) відповідає один образ функції (1.10) між (0000) і (0111), а кожному від’ємному числу А у проміжку між (- 010 ) і (-710) – одне значення оберненого коду А4ОК між (1111) і (1000).
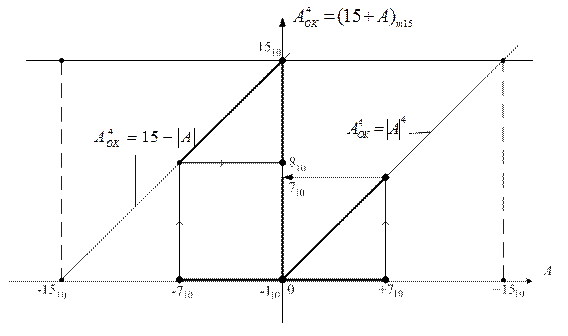
Рисунок 1.8 – Графічна інтерпретація подання чисел А із знаком
у проміжку між (-710) і (+710) чотирипозиційними оберненими
кодами 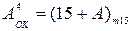
Узагальнюючи, маємо:
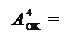
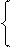 0 ХХХ, якщо (+010 ) ≤ А ≤ (+710);
0 ХХХ, якщо (+010 ) ≤ А ≤ (+710);
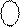
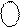
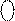 1 ХХХ, якщо (- 710 ) ≤ А ≤ ( - 010 ),
1 ХХХ, якщо (- 710 ) ≤ А ≤ ( - 010 ),
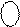 де 0 , 1 - відповідно ознака у обернених кодах позитивного і негативного стану числа – оригіналу А = ± ХХХ.
де 0 , 1 - відповідно ознака у обернених кодах позитивного і негативного стану числа – оригіналу А = ± ХХХ.
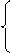 Слід звернути увагу на важливу властивість оберненого коду, яка полягає в тому, що число нуль ( 0 ) у оберненому коді згідно з ( 1.10 ) має два зображення:
Слід звернути увагу на важливу властивість оберненого коду, яка полягає в тому, що число нуль ( 0 ) у оберненому коді згідно з ( 1.10 ) має два зображення:
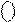
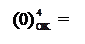 0 000, що трактується як А = (+000);
0 000, що трактується як А = (+000);
1 111, що трактується як А = ( -000).
Розглянемо типові приклади подання чисел А із знаком у обернених кодах за “арифметичним” алгоритмом (1.10).
Нехай А = - 0112 ( А = -310 ). Тоді, згідно з ( 1.10 ) маємо:
 А
А 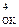 = [1510 + ( - 3)10] m15 = [ 1210] = 1 1002,
= [1510 + ( - 3)10] m15 = [ 1210] = 1 1002,
де 1 - значення знакового розряду в оберненому коді числа А=-310 (А<0).
Нехай тепер А = + 0112 (А = +310 ). Тоді згідно з (1.10 ) маємо:
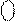
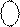 А
А 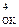 = [1510 + ( + 3)10] m15 = [ 1810]m15 = |310 |4 = 0 0112,
= [1510 + ( + 3)10] m15 = [ 1810]m15 = |310 |4 = 0 0112,
де 0 - значення знакового розряду в оберненому коді числа А=+310 (А>0). На основі “арифметичного” виразу (1.10) можна визначити також так звані «логічні» алгоритми утворення оберненого коду чисел:
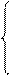 (1510 + А )4 m16 = | А |4, якщо (+710) ≥ А ≥ (+010 ); ( 1.11 )
(1510 + А )4 m16 = | А |4, якщо (+710) ≥ А ≥ (+010 ); ( 1.11 )
( А ) 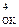 = (1510 + А )4 m16 = 1510 - | А |4 =
= (1510 + А )4 m16 = 1510 - | А |4 =
= 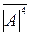 , якщо (- 710) ≤ А ≤ (- 010 ), ( 1.12 )
, якщо (- 710) ≤ А ≤ (- 010 ), ( 1.12 )
де ( А ) 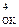 - чотирипозиційний обернений код чисел А у проміжку між (-710) і (+ 710);
- чотирипозиційний обернений код чисел А у проміжку між (-710) і (+ 710);
|А|4, 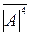 - відповідно пряме та інверсне чотирипозиційне зображення модуля аргументу А.
- відповідно пряме та інверсне чотирипозиційне зображення модуля аргументу А.
Розглянемо приклади подання цілих чисел у обернених кодах на основі «логічних» алгоритмів ( 1.11 ) і ( 1.12 ).
Нехай А = - 0012 (А = - 1). Тоді, згідно з (1.12) маємо:
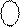
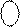 ( А )
( А ) 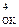 =
= 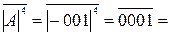 1 110, ( 1.13 )
1 110, ( 1.13 )
де 1 - стан знакового розряду оберненого коду від’ємного числа А.
 Нехай тепер А = + 1012 (А = + 510). Тоді згідно з (1.12) маємо:
Нехай тепер А = + 1012 (А = + 510). Тоді згідно з (1.12) маємо:
 ( А )
( А )  = | А |4 = | + 101 |4 = 0 101,
= | А |4 = | + 101 |4 = 0 101,
де 0 - стан знакового розряду оберненого коду числа А>0.
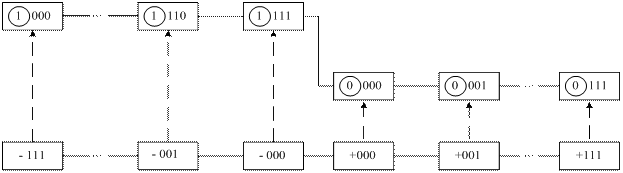
Приклади подання чисел А у проміжку між (-7) і (+7) за логічними алгоритмами ( 1.11 ) і ( 1.12) наведено на рис. 1.9.
Для спрощення виявлення випадків переповнення розрядної сітки при виконанні арифметичних операцій на суматорах використовують також модифіковане зображення звичайного оберненого коду - модифікований обернений код (МОК).
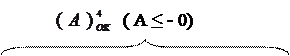
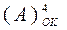 ( А ≥ + 0) ( А ≥ + 0)
| |

A ≤ - 0 A ≥ + 0
Рисунок 1.9 – Приклади подання чисел із знаком у проміжку між
(-710) і (+710) чотирипозиційними оберненими кодами 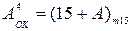
Наприклад, для чотирипозиційного формату оберненого коду ( А ) 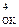 його модифіковане зображення визначається п’ятирозрядним форматом і обчислюється за формулою:
його модифіковане зображення визначається п’ятирозрядним форматом і обчислюється за формулою:
( А ) 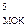 = ( 3110 + А )m31 ( 1.14 )
= ( 3110 + А )m31 ( 1.14 )
На основі “арифметичного” виразу ( 1.14 ) можна визначити «логічні» способи перетворення звичайного оберненого коду в його модифіковане зображення:
 ( А )
( А ) 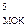 (+ 0 ≤ А ≤ + 710 ) = ( 3110 + А )m31 =
(+ 0 ≤ А ≤ + 710 ) = ( 3110 + А )m31 =
= ( 3110 + | А |3 ) m31 = 00 | А |3 = 0 А 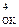 ; ( 1.15 )
; ( 1.15 )
( А ) 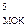 (- 710 ≤ А ≤ - 0 ) = ( 3110 + А )m31=
(- 710 ≤ А ≤ - 0 ) = ( 3110 + А )m31=
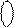 = ( 1610 + 1510 - | А |4 ) m31 = 1610 + А4ОК = 1 А
= ( 1610 + 1510 - | А |4 ) m31 = 1610 + А4ОК = 1 А 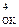 , ( 1.16 )
, ( 1.16 )
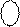
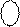 де А
де А 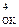 = 1510 - | А |4 = ( 1510 + А )m15, якщо А < 0;
= 1510 - | А |4 = ( 1510 + А )m15, якщо А < 0;
0 , 1 - стан знакового розряду звичайного чотирипозиційного обер- неного коду А 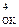 відповідно для додатних і від’ємних чисел А .
відповідно для додатних і від’ємних чисел А .
Таким чином, «логічний» алгоритм перетворення звичайного чотири-позиційного формату оберненого коду А 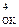 у його модифіковане зображення (А)
у його модифіковане зображення (А) 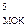 зводиться до наступного. Чотири молодших розряди модифікованого оберненого коду числа А заміщуються розрядами чотирипозиційного А
зводиться до наступного. Чотири молодших розряди модифікованого оберненого коду числа А заміщуються розрядами чотирипозиційного А 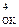 і знаковий розряд звичайного оберненого коду А
і знаковий розряд звичайного оберненого коду А 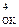 додатково дублюється у найстаршому (п’ятому) розряді модифікованого оберненого коду.
додатково дублюється у найстаршому (п’ятому) розряді модифікованого оберненого коду.
У графічній формі відображення чисел довільного знаку у проміжку між (- 710 ) і (+ 710) в МОК подано на рис. 1.10.
Приклади двійкового подання чисел у модифікованому оберненому коді за алгоритмами ( 1.15 ) і ( 1.16 ) подано на рис. 1.11.
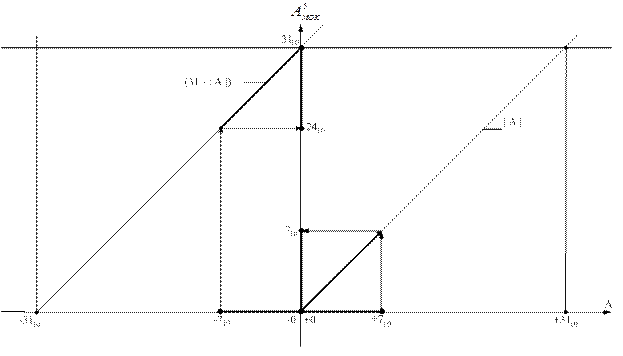
Рисунок 1.10 – Графічна інтерпретація подання чисел А із знаком
у проміжку між (-710) і (+710) п’ятипозиційними модифікованими
оберненими кодами (МОК)
| | | | |
| | 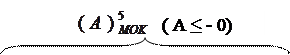 |
| | | 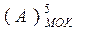 ( А ≥ + 0) ( А ≥ + 0)
| |
| |
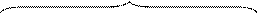
A ≤ - 0 A ≥ + 0
Рисунок 1.11 – Приклади подання цілих чисел А із знаком у проміжку
між (-710) і (+710) п’ятипозиційними модифікованими оберненими кодами


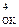 = (1510 + А ) m15, ( 1.10 )
= (1510 + А ) m15, ( 1.10 )
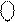
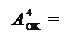
 0 ХХХ, якщо (+010 ) ≤ А ≤ (+710);
0 ХХХ, якщо (+010 ) ≤ А ≤ (+710);
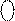 1 ХХХ, якщо (- 710 ) ≤ А ≤ ( - 010 ),
1 ХХХ, якщо (- 710 ) ≤ А ≤ ( - 010 ),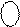 де 0 , 1 - відповідно ознака у обернених кодах позитивного і негативного стану числа – оригіналу А = ± ХХХ.
де 0 , 1 - відповідно ознака у обернених кодах позитивного і негативного стану числа – оригіналу А = ± ХХХ.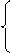 Слід звернути увагу на важливу властивість оберненого коду, яка полягає в тому, що число нуль ( 0 ) у оберненому коді згідно з ( 1.10 ) має два зображення:
Слід звернути увагу на важливу властивість оберненого коду, яка полягає в тому, що число нуль ( 0 ) у оберненому коді згідно з ( 1.10 ) має два зображення: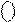
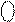
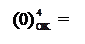 0 000, що трактується як А = (+000);
0 000, що трактується як А = (+000);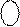
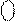
 А
А  (1510 + А )4 m16 = | А |4, якщо (+710) ≥ А ≥ (+010 ); ( 1.11 )
(1510 + А )4 m16 = | А |4, якщо (+710) ≥ А ≥ (+010 ); ( 1.11 )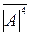 , якщо (- 710) ≤ А ≤ (- 010 ), ( 1.12 )
, якщо (- 710) ≤ А ≤ (- 010 ), ( 1.12 ) ( А )
( А ) 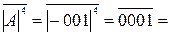 1 110, ( 1.13 )
1 110, ( 1.13 ) Нехай тепер А = + 1012 (А = + 510). Тоді згідно з (1.12) маємо:
Нехай тепер А = + 1012 (А = + 510). Тоді згідно з (1.12) маємо:
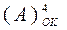 ( А ≥ + 0)
( А ≥ + 0)


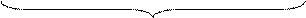
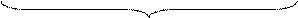
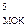 = ( 3110 + А )m31 ( 1.14 )
= ( 3110 + А )m31 ( 1.14 ) ( А )
( А )  = ( 1610 + 1510 - | А |4 ) m31 = 1610 + А4ОК = 1 А
= ( 1610 + 1510 - | А |4 ) m31 = 1610 + А4ОК = 1 А 

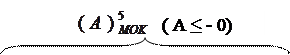
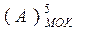 ( А ≥ + 0)
( А ≥ + 0)