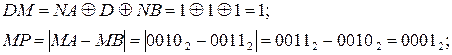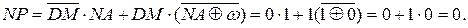Для визначенності розглянемо подання чисел у чотирирозрядному процесорі.
Зміщений код цілих чисел А із знаком у формі з негативним нулем у цьому випадку буде визначатися співвідношенням:
(А ) 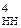 = 710 + А , ( 1.22 )
= 710 + А , ( 1.22 )
де 4 – довжина розрядної сітки машинного коду з негативним нулем (ХХХХ);
710 = (2310 – 1 ) = (2(4-1)-1) – параметр відображення (зміщення) коду з негативним нулем за чотирипозиційним форматом.
Із “арифметичного” виразу (1.22) випливає область визначення чотири-позиційного зміщеного коду з негативним кодуванням нуля:
А = (А ) 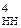 - 710 = (00002 ¸ 11112) – 710 =
- 710 = (00002 ¸ 11112) – 710 =
= (0 ¸1510 ) – 710 = (- 710) ¸ (+ 810) . ( 1.23 )
У графічній формі функцію (1.22) для інтервалу її визначення подано на рис.1.14.
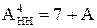
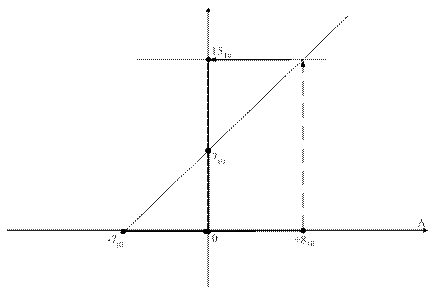
Рисунок 1.14 – Графічна інтерпретація подання чотирипозиційними кодами з негативним нулем цілих чисел А у проміжку між (-710) і (+810)
Розглянемо типові приклади перетворення цілих чисел із знаком у змі-щений код з негативним кодуванням нуля на основі “арифметичного” алгоритму (1.22).
Нехай А = + 1012 ( +510 ). Тоді згідно з ( 1.22 ) маємо:
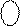 (А )
(А ) 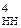 = [710 + А]4 = [ 710 + (+1012)]4 = [ 710 + (+510)]4 = [1210]4 = 1 1002.
= [710 + А]4 = [ 710 + (+1012)]4 = [ 710 + (+510)]4 = [1210]4 = 1 1002.
Нехай тепер В = - 1012. Тоді згідно з (1.23 ) маємо :
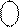 (В )
(В ) 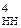 = [710 + В]4 = [ 710 + (- 1012)]4 = [ 710 + (-510)]4 = [210]4 = 0 0102.
= [710 + В]4 = [ 710 + (- 1012)]4 = [ 710 + (-510)]4 = [210]4 = 0 0102.
На основі “арифметичного” виразу функції ( 1.22 ) можна визначити “логічнi” алгоритми утворення зміщеного коду з негативним нулем цілих чисел А:
(А ) 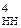 [(+ 00012) ≤ А ≤ (+ 10002)] = (710 + А)4 =
[(+ 00012) ≤ А ≤ (+ 10002)] = (710 + А)4 =
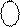
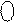 = [810 + (A – 1)]4 = 1 [A – 1]3 = 1 [|A| – 1]3 ; ( 1.24 )
= [810 + (A – 1)]4 = 1 [A – 1]3 = 1 [|A| – 1]3 ; ( 1.24 )
(А ) 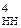 [(- 1112) ≤ А ≤ (- 0002)] = (710 + А)4 =
[(- 1112) ≤ А ≤ (- 0002)] = (710 + А)4 =
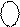 = [ 710 - | A |3 ]4 = 0
= [ 710 - | A |3 ]4 = 0 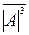 , ( 1.25 )
, ( 1.25 )
де [|A| – 1]3 – трипозиційний код декремента модуля додатних цілих чисел А у проміжку між (+ 0012) і (+ 10002);
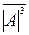 - трипозиційний код порозрядної інверсії модуля від’ємних чисел А у проміжку між (- 1112) і (- 0002);
- трипозиційний код порозрядної інверсії модуля від’ємних чисел А у проміжку між (- 1112) і (- 0002);
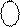
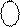 1 , 0 - стан знакового розряду коду з негативним нулем відповідно для додатного і від’ємного значення аргументу А функції (1.22).
1 , 0 - стан знакового розряду коду з негативним нулем відповідно для додатного і від’ємного значення аргументу А функції (1.22).
Розглянемо приклади перетворення цілих чисел у зміщений код з нега-тивним нулем на основі побудованих «логічних» алгоритмів (1.24) і (1.25).
Нехай А = - 0112 ( - 310 ). Тоді згідно з ( 1.25 ) маємо:
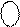
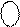
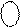
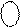 (А )
(А ) 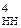 = 0
= 0 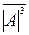 = 0
= 0 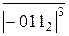 = 0
= 0 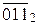 = 0 1002. ( 1.26 )
= 0 1002. ( 1.26 )
Нехай В = + 1102 (В = + 610 ). Тоді згідно з ( 1.24 ) маємо:
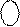
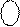
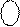
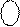 (В )
(В ) 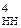 = 1 [|B| - 1]4 = 1 [1102 - 1]3 = 1 [1012]3 = 1 1012.
= 1 [|B| - 1]4 = 1 [1102 - 1]3 = 1 [1012]3 = 1 1012.
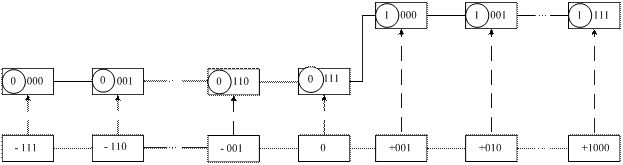
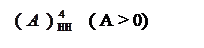 Приклади двійкового зображення чисел А із знаком у зміщеному коді з негативним кодуванням нуля для області визначення функції (1.22) подано на рис.1.15.
Приклади двійкового зображення чисел А із знаком у зміщеному коді з негативним кодуванням нуля для області визначення функції (1.22) подано на рис.1.15.
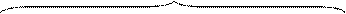
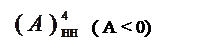
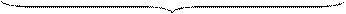
A < 0 A > 0
Рисунок 1.15 – Приклади подання цілих чисел А із знаком у проміжку між (-710) і (+810) чотирипозиційними зміщеними кодами
 Із рис.1.15 випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А)
Із рис.1.15 випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А) 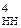 (крайній зліва розряд у коді (А)
(крайній зліва розряд у коді (А) 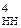 ), а множина від’ємних чисел А – цифрою 0 у знаковому розряді коду з негатив-ним нулем. Зазначимо, що нульове значення аргументу А (А=0) відображає-ться у знаковому розряді (А)
), а множина від’ємних чисел А – цифрою 0 у знаковому розряді коду з негатив-ним нулем. Зазначимо, що нульове значення аргументу А (А=0) відображає-ться у знаковому розряді (А) 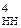 цифрою 0, тобто як негативне ціле число (- 0). Таким чином, числова множина ( 0 0002 ¸ 0 1112) функції (А)
цифрою 0, тобто як негативне ціле число (- 0). Таким чином, числова множина ( 0 0002 ¸ 0 1112) функції (А) 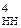 відображає проміжок чисел між (-710) і (- 0), а числова множина ( 1 0002 ¸ 1 1112) функції (А)
відображає проміжок чисел між (-710) і (- 0), а числова множина ( 1 0002 ¸ 1 1112) функції (А) 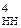 – проміжок чисел між (+110 ) і (+810 ).
– проміжок чисел між (+110 ) і (+810 ).
1.2 Теоретичні засади та структура арифметичних пристроїв
для додавання і віднімання чисел у прямих кодах
1.2.1 Алгоритми додавання і віднімання чисел у прямих кодах
У загальному випадку операція додавання і віднімання, наприклад, п’ятипозиційних прямих кодів визначається формулою:
P  = А
= А  (D) B
(D) B  , ( 1.27 )
, ( 1.27 )
де А  , B
, B  - зображення чисел із знаком у прямих кодах за п’ятипози-ційним форматом, які беруть участь в операції алгебричного додавання (за D = 0) або віднімання (за D = 1);
- зображення чисел із знаком у прямих кодах за п’ятипози-ційним форматом, які беруть участь в операції алгебричного додавання (за D = 0) або віднімання (за D = 1);
P  – результат операції у прямому коді.
– результат операції у прямому коді.
 Припустімо, що :
Припустімо, що :

 АПК = NA MA; BПК = NB MB;
АПК = NA MA; BПК = NB MB;  PПК = NP MP,
PПК = NP MP,

 де NA , NВ , NР - стан знакового розряду відповідно операндів А і В та результату Р алгебричної дії;
де NA , NВ , NР - стан знакового розряду відповідно операндів А і В та результату Р алгебричної дії;
МA(4/1), МВ(4/1), МР(4/1) - модулі операндів А і В та результату Р операції (1.27) за чотирипозиційним форматом.
Звичайні правила виконання операцій алгебричного додавання і віднімання чисел у прямих кодах подано в табл.1.1.
Таблиця 1.1 - Алгоритм додавання (за D = 0) і віднімання (за D = 1) чисел
у прямих кодах
|
NA
|
D
|
NB
|
DM
|
MP
| NP
|
| MA ≥ MB
(ω = 1)
| MA < MB
(ω = 0)
|
|
|
|
|
| MA = MB
| 0 (NA)
| 0 (NB)
|
|
|
|
|
| |MA – MB|
| 0 (NA)
| 1 (NB)
|
|
|
|
|
| |MA – MB|
| 1 (NA)
| 0 (NB)
|
|
|
|
|
| MA + MB
| 1 (NA)
| 1 (NB)
|
|
|
|
|
| |MA – MB|
| 0 (NA)
| 1( 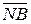 ) )
|
|
|
|
|
| MA + MB
| 0 (NA)
| 0( 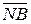 ) )
|
|
|
|
|
| MA + MB
| 1 (NA)
| 1( 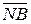 ) )
|
|
|
|
|
| |MA – MB|
| 1 (NA)
| 0( 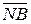 ) )
|
Згідно з табл.1.1 і карти Карно (рис.1.16) логічний вираз для обчислення кода операції над модулями (DМ ) операндів має вигляд:
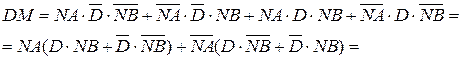
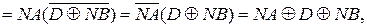 ( 1.28 )
( 1.28 )
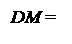
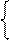 де 0, якщо МР = МА + МВ ; ( 1.29 )
де 0, якщо МР = МА + МВ ; ( 1.29 )
1, якщо МР = |МА - МВ|. ( 1.30 )
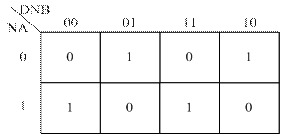
DМ
Рисунок 1.16 - Карта Карно для визначення коду операції
над модулями чисел у прямих кодах (табл.1.1):
DM – визначає відповідно операцію додавання (за DM = 0) і віднімання (за DМ = 1)модулів чисел у прямих кодах;
D – логічна змінна для кодування операції додавання (за D = 0) і віднімання (за D = 1) чисел А і В у прямих кодах;
NA, NB – відповідно знакові розряди першого (А) та другого (В) оперaнда в прямих кодах.
Для обчислення знакового розряду результату NP запровадимо ознаку відношення модулів операндів (табл.1.1) :
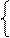
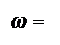 1, якщо МА ≥ МВ;
1, якщо МА ≥ МВ;
0, якщо МА < MВ. ( 1.31 )
Тоді алгоритм обчислення правильного знака результату (табл.1.1) приймає вигляд таблиці 1.2. Відповідна карта Карно для мінімізації функції знака результату NP показана на рис.1.17. Із побудованої карти Карно можна отримати дві форми рівняння для обчислення знака результату NP :
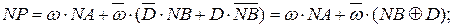 ( 1.32 )
( 1.32 )
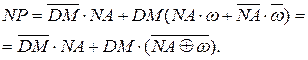 ( 1.33 )
( 1.33 )
Слід вказати на відмінність виразів ( 1.32 ) і ( 1.33 ).
Логічне рівняння (1.32) визначає стан знакового розряду результату залежно від чотирьох змінних: NA, NB, ω та D. Для обчислення знака результату за формулою ( 1.33 ) необхідно опрацьовувати тільки три змінні: 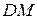 , ω та NA. Очевидно, співвідношення (1.33) можна записати також у спрощеному вигляді:
, ω та NA. Очевидно, співвідношення (1.33) можна записати також у спрощеному вигляді:
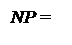
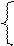 NA, якщо
NA, якщо 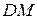 = 0 або
= 0 або 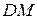 = 1 і ω = 1;
= 1 і ω = 1;
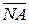 , якщо
, якщо 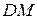 =1 і ω =0. ( 1.34 )
=1 і ω =0. ( 1.34 )
Таблиця 1.2 - Алгоритм формування знака результату при додаванні
(за D = 0) і відніманні (за D = 1) чисел у прямих кодах
| NA
| D
| NB
| DM
| ω
| NP (знаковий біт результату)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| *
| *
| *
| *
| *
| *
|
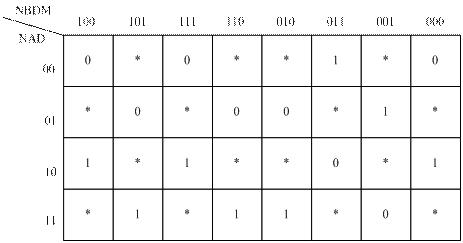
NP
Рисунок 1.17 – Карта Карно для мінімізації функції
визначення знака результату (табл.1.2):
* - заборонені комбінації вхідних змінних D, ω, NA, NB, DM;
NP - знаковий біт результату.
Обчислення модуля результату МР зводиться до додавання (за 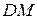 =0) або віднімання (за
=0) або віднімання (за 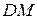 = 1) модулів операндів (табл.1.1):
= 1) модулів операндів (табл.1.1):

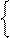 МA + МВ, якщо
МA + МВ, якщо 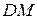 = 0;
= 0;
|МA - МВ|, якщо 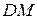 =1,
=1,
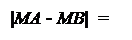
 де МA – МВ, якщо МA ≥ МВ ;
де МA – МВ, якщо МA ≥ МВ ;
МВ - МA, якщо МA < МВ.
Узагальнюючи, маємо:
 (МA + МВ), якщо
(МA + МВ), якщо 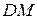 = 0; ( 1.35 )
= 0; ( 1.35 )
МP = (МA – МВ), якщо 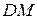 =1 і (МA ≥ МВ); ( 1.36 ) (МВ - МА), якщо
=1 і (МA ≥ МВ); ( 1.36 ) (МВ - МА), якщо 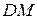 =1 і (МA < МВ ). ( 1.37 )
=1 і (МA < МВ ). ( 1.37 )
Таким чином, згідно з (1.35) – (1.37) алгоритм обчислення модуля результату МР вимагає виконання в арифметичному пристрої як операції підсумовування модулів операндів за формулою (1.36), так і обчислення різниці модулів, тобто віднімання модулів операндів за формулою (1.36) або (1.37) залежно від значення ознаки відношення модулів операндів ( ω ).
Розглянемо типові приклади виконання операцій додавання та віднімання прямих кодів чисел А і В за побудованим алгоритмом.
Нехай D = 0, NA = 0, MA = 00102, NB =1, MB = 00112. Тоді маємо:
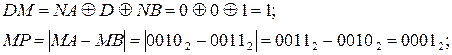
ω( MB > MA ) = 0;
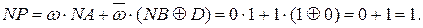
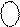 Таким чином, остаточно маємо
Таким чином, остаточно маємо 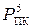 = 1 0001.
= 1 0001.
Нехай тепер D = 1, NA = 1, MA = 00102, NB =1, MB = 00112. Тоді маємо:
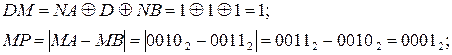
ω( MB > MA ) = 0;
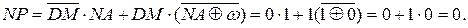
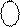 Таким чином, остаточно маємо
Таким чином, остаточно маємо 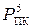 = 0 0001.
= 0 0001.


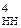 = 710 + А , ( 1.22 )
= 710 + А , ( 1.22 )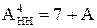

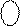 (А )
(А ) 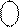 (В )
(В ) 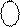
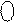 = [810 + (A – 1)]4 = 1 [A – 1]3 = 1 [|A| – 1]3 ; ( 1.24 )
= [810 + (A – 1)]4 = 1 [A – 1]3 = 1 [|A| – 1]3 ; ( 1.24 )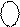 = [ 710 - | A |3 ]4 = 0
= [ 710 - | A |3 ]4 = 0 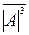 , ( 1.25 )
, ( 1.25 )
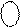
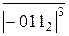 = 0
= 0 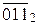 = 0 1002. ( 1.26 )
= 0 1002. ( 1.26 )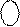
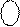
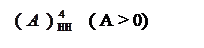 Приклади двійкового зображення чисел А із знаком у зміщеному коді з негативним кодуванням нуля для області визначення функції (1.22) подано на рис.1.15.
Приклади двійкового зображення чисел А із знаком у зміщеному коді з негативним кодуванням нуля для області визначення функції (1.22) подано на рис.1.15.
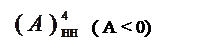

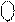
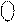 Із рис.1.15 випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А)
Із рис.1.15 випливає, що множина додатних чисел А характеризується цифрою 1 у знаковому розряді (А) 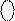
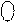
 = А
= А  Припустімо, що :
Припустімо, що :
 АПК = NA MA; BПК = NB MB;
АПК = NA MA; BПК = NB MB;  PПК = NP MP,
PПК = NP MP,
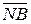 )
)
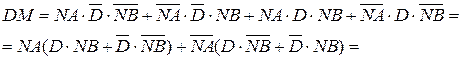
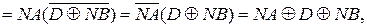 ( 1.28 )
( 1.28 )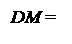
 де 0, якщо МР = МА + МВ ; ( 1.29 )
де 0, якщо МР = МА + МВ ; ( 1.29 )
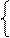
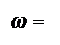 1, якщо МА ≥ МВ;
1, якщо МА ≥ МВ;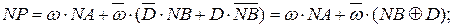 ( 1.32 )
( 1.32 )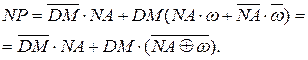 ( 1.33 )
( 1.33 )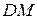 , ω та NA. Очевидно, співвідношення (1.33) можна записати також у спрощеному вигляді:
, ω та NA. Очевидно, співвідношення (1.33) можна записати також у спрощеному вигляді: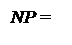
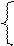 NA, якщо
NA, якщо 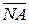 , якщо
, якщо 

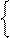 МA + МВ, якщо
МA + МВ, якщо 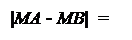
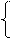 де МA – МВ, якщо МA ≥ МВ ;
де МA – МВ, якщо МA ≥ МВ ;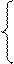 (МA + МВ), якщо
(МA + МВ), якщо 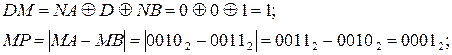
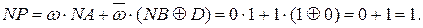
 Таким чином, остаточно маємо
Таким чином, остаточно маємо 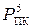 = 1 0001.
= 1 0001.