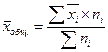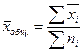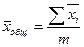21. Задание {{ 323 }} ТЗ № 323
Дисперсия альтернативного признака ...
£ 0,5 < 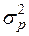 £ 1
£ 1
£ 0 £ 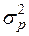 £
£ 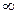
£ 0 £ 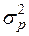 £ 0,25
£ 0,25
£ 0,25 £ 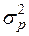 £ 1
£ 1
22. Задание {{ 22 }} ТЗ-1-22.
Показателями структуры вариационного ряда являются: ... .
£ простая средняя арифметическая
£ средняя арифметическая взвешенная
£ мода
£ медиана
£ среднее квадратическое отклонение
£ дисперсия
£ дециль
£ квартиль.
23. Задание {{ 23 }} ТЗ-1-23.
При увеличении всех значений признака в 2 раза средняя величина признака ... .
£ не изменится
£ увеличится в 2 раза
£ уменьшится в 2 раза
£ увеличится более чем в 2 раза
£ уменьшится более чем в 2 раза
24. Задание {{ 24 }} ТЗ-1-24.
При уменьшении значений частот в средней арифметической взвешенной в 2 раза значение средней величины признака ... .
£ не изменится
£ увеличится в 2 раза
£ уменьшится в 2 раза
£ увеличится более чем в 2 раза
£ уменьшится более чем в 2 раза
25. Задание {{ 26 }} ТЗ-1-26.
Модой называется ... .
£ среднее значение признака в данном ряду распределения
£ наиболее часто встречающееся значение признака в данном ряду
£ значение признака, делящее данную совокупность на две равные части
£ наиболее редко встречающееся значение признака в данном ряду
£ серединное значение признака в данном ряду распределения
26. Задание {{ 27 }} ТЗ-1-27.
Соответствие между видом средней величины и ее формулой:
| средняя арифметическая взвешенная
| 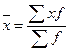
|
| простая средняя арифметическая
| 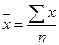
|
| средняя гармоническая взвешенная
| 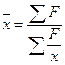
|
| простая средняя гармоническая
| 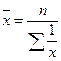
|
27. Задание {{ 28 }} ТЗ-1-28.
Сумма отклонений индивидуальных значений признака от их средней величины ... .
£ больше нуля
£ меньше нуля
£ равна нулю
£ больше или равна нулю
£ меньше или равна нулю
28. Задание {{ 29 }} ТЗ-1-29.
Формулы для расчета дисперсии признака: ... .
£ 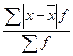
£ 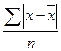
£ 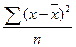
£ 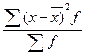
£ 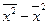
29. Задание {{ 30 }} ТЗ-1-30.
Правило мажорантности средних определяется как:
где 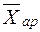 - средняя арифметическая;
- средняя арифметическая;
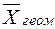 - средняя геометрическая;
- средняя геометрическая;
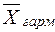 - средняя гармоническая;
- средняя гармоническая;
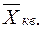 - средняя квадратическая.
- средняя квадратическая.
£ 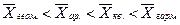
£ 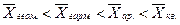
£ 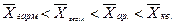
£ 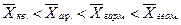
£ 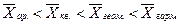
30. Задание {{ 31 }} ТЗ-1-31.
Средняя величина признака равна 20, а коэффициент вариации -25 %.
Дисперсия признака равна ... .
31. Задание {{ 32 }} ТЗ-1-32.
Медианой называется ... .
£ среднее значение признака в ряду распределения
£ наиболее часто встречающееся значение признака в данном ряду
£ значение признака, делящее совокупность на две равные части
£ наиболее редко встречающееся значение признака в данном ряду
£ значения признака, делящие совокупность на четыре равные части
32. Задание {{ 33 }} ТЗ-1-33.
Средняя величина признака равна 22,
а коэффициент вариации признака - 26 %.
Дисперсия признака (с точностью до 0,0001) равна ... .
33. Задание {{ 34 }} ТЗ-1-34.
По ряду распределения:
Группы семей по размеру жилой
площади, приходящейся на 3-5 5-7 7-9 9-11 11-13
одного человека, кв.м
Число семей с данным размером
жилой площади10 21 28 30 26
Мода (с точностью до 0.1) равна …
34. Задание {{ 35 }} ТЗ-1-34.
Ряд распределения:
Группы семей по размеру жилой
площади, приходящейся на
одного человека, кв.м. 3-5 5-7 7-9 9-11 11-13
Число семей с данным размером
жилой площади10 21 28 30 26
Медиана (с точностью до 0.1) равна …
35. Задание {{ 36 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Вид данного ряда - ... .
£ дискретный
£ интервальный
£ атрибутивный
36. Задание {{ 37 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Cредний тарифный разряд рабочих = ... (с точностью до 0,1).
37. Задание {{ 316 }} ТЗ-1-25.
Дисперсия альтернативного признака - ... .
£ 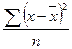
£ 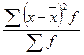
£ 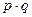
£ 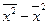
38. Задание {{ 38 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Мода = ... (с точностью до 0,1):
Правильные варианты ответа: 4; 4,0;
39. Задание {{ 39 }} ТЗ-1-35.
Имеется ряд распределения:
Тарифный разряд рабочих: 2 3 4 5 6
Число рабочих: 8 16 17 12 7
Медиана = ... (с точностью до 0,1).
Правильные варианты ответа: 4; 4,0;
40. Задание {{ 40 }} ТЗ-1-36.
Абсолютные показатели вариации: ... .
£ размах вариации
£ коэффициент корреляции
£ коэффициент осциляции
£ среднее линейное отклонение
£ среднее квадратическое отклонение
£ дисперсия
£ коэффициент вариации.
41. Задание {{ 41 }} ТЗ-1-37.
По результатам экзамена по статистике медиана равна:
| Балл оценки
знаний студентов
|
(неудовлетво
рительно)
|
(удовлетво
рительно)
|
(хорошо)
|
(отлично)
|
| Число студентов
|
|
|
|
|
42. Задание {{ 42 }} ТЗ-1-38.
Правило сложения дисперсий выражается формулой ... .
£ 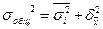
£ 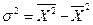
43. Задание {{ 43 }} ТЗ-1-39.
Размах вариации - это ... .
£ R = Хmax - 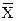
£ R = 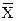 - Хmin
- Хmin
£ R = Хmax - Хmin
£ R = Х - Хmin
44. Задание {{ 44 }} ТЗ-1-40.
Средний курс продажи одной акции по данным о торгах на фондовой бирже (с точностью до целых) равен …
| Сделка
| Количество проданных акций, шт.
| Курс продажи, руб.
|
|
|
|
|
45. Задание {{ 45 }} ТЗ-1-41.
Дисперсия рассчитывается как ... .
£ 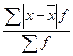
£ 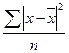
£ 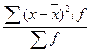
£ 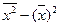
£ 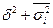
46. Задание {{ 46 }} ТЗ-1-42.
Если модальное значение признака больше средней величины признака, то это свидетельствует о ... .
£ правосторонней асимметрии в данном ряду распределения
£ левосторонней асимметрии в данном ряду распределения
£ симметричности распределения;
£ нормальном законе распределения
£ биномиальном законе распределения
47. Задание {{ 47 }} ТЗ-1-43.
Относительные показатели вариации ... .
£ размах вариации
£ дисперсия
£ коэффициент вариации
£ среднее линейное отклонение
£ относительное линейное отклонение
48. Задание {{ 48 }} ТЗ-1-44.
Средняя величина признака равна 22,
а дисперсия признака - 36.
Коэффициент вариациит = ... (с точностью до 0,1 %)
49. Задание {{ 49 }} ТЗ-1-45.
Статистическая совокупность разбита на m групп по факторному признаку.
В каждой группе исчислено среднее значение результативного признака: 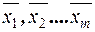 ,
,
численность единиц в каждой группе n1, n2, …,nm.
Среднее значение в целом по совокупности определяется как ... .
£ 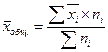
£ 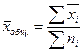
£ 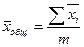
50. Задание {{ 50 }} ТЗ-1-46.
Значение моды определяется на основе графика ... .
£ полигона распределения
£ функции распределения
£ кумуляты
£ огивы
£ кривой Лоренца
51. Задание {{ 51 }} ТЗ-1-47.
Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300
на I/V - 2002 г. - 320
на I/VI - 2002 г. - 310
на I/VII - 2002 г. - 290
Cредний остаток оборотных средств (с точностью до 0,1 млн.руб.) за 2 квартал = ... млн. руб.
£ 305
£ 310
£ 308,3
£ 312,5
52. Задание {{ 52 }} ТЗ-1-48.
Данные на начало месяцев (млн. руб.):
на I/IV -2002 г. - 300
на I/V - 2002 г. - 320
на I/VI - 2002 г. - 310
на I/VII - 2002 г. - 290
для расчета среднего остатка оборотных средств за 2 квартал следует применить среднюю... .
£ гармоническую
£ геометрическую
£ хронологическую
£ степенную
£ арифметическую
53. Задание {{ 53 }} ТЗ-1-49
Средний уровень издержек обращения на 100 руб. товарооборота по следующим данным(с точностью до 0,1 руб.):
| Издержки обращения на 100 руб. товарооборота, руб.
| Число предприятий
| Товарооборот в среднем на одно предприятие, млн. руб.
|
| до 2
2 - 4
4 - 6
6 и выше
|
|
|
54. Задание {{ 54 }} ТЗ-1-50.
Средний размер товарооборота на одно предприятие по следующим данным (с точностью до 0,1 млн. руб.):
| Издержки обращения на 100 руб. товарооборота, руб.
| Число предприятий
| Товарооборот в среднем на одно предприятие, млн. руб.
|
| до 2
2 - 4
4 - 6
6 и выше
|
|
|
55. Задание {{ 55 }} ТЗ-1-51.
Мода по данным о распределении работников предприятия по размеру месячной заработной платы равна …
| Группы работников по размеру заработной платы, руб.
| Число работников
|
|
|
|
56. Задание {{ 56 }} ТЗ-1-52.
Медиана по данным о распределении работников предприятия по размеру месячной заработной платы равна …
| Группы работников по размеру заработной платы, руб.
| Число работников
|
|
|
|
57. Задание {{ 58 }} ТЗ-1-54.
Для значений признака: 3, 5, 6, 9, 11, 12, 13
Мода ... .
£ отсутствует
£ равна 3
£ равна 13
£ равна 9
£ равна 6
58. Задание {{ 59 }} ТЗ-1-55.
Для следующих значений признака: 3, 3, 3, 4, 4, 6, 7, 9, 9
Мода ... .
£ мода отсутствует
£ равна 3
£ равна 4
£ равна 9
£ равна 6
59. Задание {{ 60 }} ТЗ-1-56.
Средний квадрат индивидуальных значений признака равен 625,
а его дисперсия - 400.
Величина средней = ... .
60. Задание {{ 61 }} ТЗ-1-57.
При осмотре партии деталей среди них оказалось 2 % бракованных.
Дисперсия = ... .
61. Задание {{ 62 }} ТЗ-1-58.
При осмотре партии деталей среди них оказалось 10 бракованных изделий.
Если в полученной партии было 200 изделий, то дисперсия = ... .

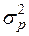 £ 1
£ 1
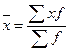
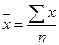
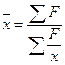
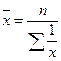
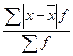
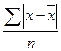
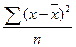
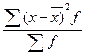
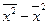
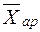 - средняя арифметическая;
- средняя арифметическая;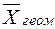 - средняя геометрическая;
- средняя геометрическая;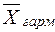 - средняя гармоническая;
- средняя гармоническая;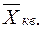 - средняя квадратическая.
- средняя квадратическая.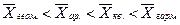
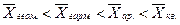
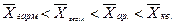
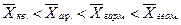
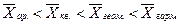
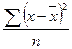
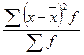
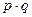
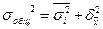
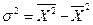
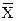
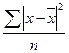
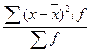
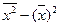
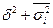
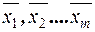 ,
,