Переходная функция апериодического звена I-ого порядка имеет вид:
h(t) = L-1[W(s)·1(t)] = L-1[K/(s·(T·s + 1))] = K – K·e-t/T = K·(1 – e-t/T)
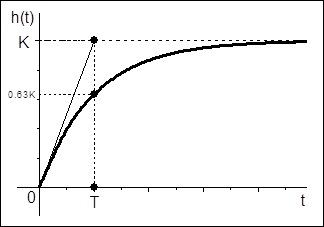

Рис. 3.6. Переходная характеристика апериодического звена I-го порядка.
Переходный процесс апериодического звена I-ого порядка имеет экспоненциальный вид. Установившееся значение равно: hуст = K. Касательная в точке t = 0 пересекает линию установившегося значения в точке t = T. В момент времени t = T переходная функция принимает значение: h(T) ≈ 0.632·K, т.е. за время T переходная характеристика набирает только около 63% от установившегося значения.
Определим время регулирования Tу для апериодического звена I-ого порядка. Как известно из предыдущей лекции, время регулирования – это время, после которого разница между текущим и установившимся значениями не будет превышать некоторой заданной малой величины Δ. (Как правило, Δ задается как 5 % от установившегося значения).
h(Tу) = (1 – Δ)·hуст = (1 – Δ)·K = K·(1 – e-Tу/T), отсюда е-Tу/T = Δ, тогда Tу/T = -ln(Δ), В итоге получаем Tу = [-ln(Δ)]·T.
При Δ = 0,05 Tу = - ln(0.05)·T ≈ 3·T.
Другими словами, время переходного процесса апериодического звена I-ого порядка приблизительно в 3 раза превышает постоянную времени.