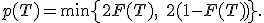Обозначим через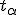 
значение, которое находится из уравнения 
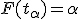, где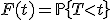 
— функция распределения статистики 
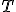. Если функция распределения непрерывная строго монотонная, то 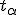есть обратная к ней функция:
.
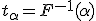Значение 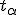называется также 
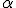-квантилем распределения 
.
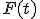На практике, как правило, используются статистики 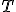с унимодальной (имеющей форму пика) плотностью распределения. Критические области (наименее вероятные значения статистики) соответствуют «хвостам» этого распределения. Поэтому чаще всего возникают критические области одного из трёх типов:
§ Левосторонняя критическая область:
определяется интервалом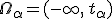 
.
пи-величина: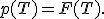 
§ Правосторонняя критическая область:
определяется интервалом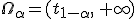 
.
пи-величина: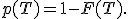 
§ Двусторонняя критическая область:
определяется двумя интервалами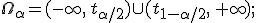 
пи-величина: 
