Соотношения в Булевой алгебре. Функциональные схемы элементарной логики. Функции, таблицы истинности.
Две формулы булевой алгебры равносильны (равны, эквивалентны), если равны сопоставляемые им функции (т.е. они принимают одинаковые значения на всех наборах значений аргументов). Ниже даны основные законы булевой алгебры, позволяющие проводить тождественные преобразования формул булевой алгебры (обратите внимание, насколько они похожи на законы классической арифметики): Законы и тождества алгебры логики
Математический аппарат алгебры логики позволяет преобразовать логическое выражение, заменив его равносильным с целью упрощения, сокращения числа элементов или замены элементной базы.
Законы:
1 Переместительный: X ∨ Y = Y ∨ X; X · Y = Y · X.
2 Cочетательный: X ∨ Y ∨ Z = (X ∨ Y) ∨ Z = X ∨(Y ∨ Z); X · Y · Z = (X · Y) · Z = X· (Y· Z).
3 Идемпотентности: X ∨ X = X; X · X = X.
4 Распределительный: (X ∨ Y)· Z = X· Z ∨ Y· Z.
5 Двойное отрицание: 
.
6 Закон двойственности (Правило де Моргана):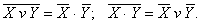 
Для преобразования структурных формул применяется ряд тождеств:
X ∨ X · Y = X; X(X ∨ Y) = X — Правила поглощения.
X· Y ∨ X· 
= X, (X ∨ Y)·(X ∨ ) = X – Правила склеивания.
