Как видим, одна логическая функция может быть представлена, по крайней мере, двумя формулами – СДНФ и СКНФ. Из этих формул путем преобразований (например, при минимизации) можно получить еще ряд формул в дизъюнктивной нормальной форме (ДНФ) или в конъюнктивной нормальной форме (КНФ).
Дизъюнктивной нормальной формой логической функции называется дизъюнкция любого числа элементарных конъюнкций.
Конъюнктивной нормальной формой логической функции называется конъюнкция любого числа элементарных дизъюнкций.
В качестве примера проведем преобразования функции
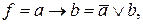
представленной СКНФ.
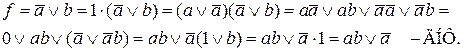
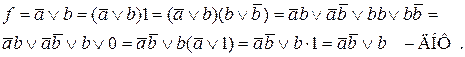
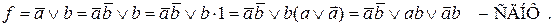
Таким образом, одна логическая функция может иметь несколько формул, но одна формула всегда описывает одну логическую функцию. В этом различие понятий логической функции и формулы, ее представляющей.