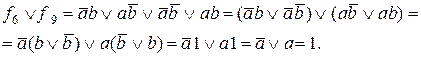У каждой логической функции есть инверсная функция.
Инверсная функция – это функция, значения которой на каждом входном наборе инверсны значениям прямой функции.
Если функция задана таблицей истинности, то ее инверсная функция получается заменой в графе функции 0 на 1, а 1 на 0. Произведя аналогичные действия над значениями инверсной функции, можно получить прямую функцию. Какую функцию считать прямой, а какую инверсной – это определяет разработчик.
Инверсная функция для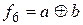 
(табл. 5) обозначается как 
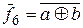, а ее таблица истинности приведена в табл. 8. Это функция 
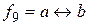– эквивалентность.
По определению Теории множеств (да и по обозначению) инверсная функция булевой алгебры это не что иное, как дополнение прямой функции до единицы. Действительно, для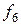 
получаем
