x=(0101) 
=(1010)
Булева функция называется самодвойственной, если она является двойственной по отношению к самой себе, то есть принимает противоположные значения на противоположных наборах аргументов.
Пример 3.3. Самодвойственной функции является: у= . Не самодвойственные функции: у=х1*х2; у=х1Vх2; у=х1Åх2.
Принадлежность базовых булевых функций и логических констант к замечательным классам представлена таблицей.
К0 (+) сохраняет константу ноль, (-) не сохраняет константу ноль;
К1 (+) сохраняет константу единица, (-) не сохраняет константу;
Кл (+) линейная ,(-) нелинейная;
Км (+) монотонная , (-) не монотонная;
Кс (+) самодвойственная, (-) не самодвойственная.
Таблица 3.1.
| Функция
| К0
| К1
| Кл
| Км
| Кс
|
| 0
| +
| -
| +
| +
| -
|
| 1
| -
| +
| +
| +
| -
|
| -
|
|
|
|
|
| +
| +
| -
| +
| -
|
| +
| +
|
| +
| -
|
| +
| -
| +
| -
| -
|
| -
|
| +
|
| -
|
| +
|
|
| -
|
|
| -
|
|
|
|
|
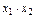
| х1|х2
| -
|
| -
|
|
|
| -
|
|
|
|
|
